Last Updated on 2025-12-09 by BallPen
변분의 개념을 알아보고 미분과의 차이점을 이해해 봐요.
변분(variation)이란 함수의 모양이 아주 조금씩 변할 때(\delta y), 출력값(S)가 얼마나 변하는지(\delta S)를 계산하는 것을 말합니다.
반면에 미분이란 입력값(x)이 아주 조금씩 변할 때, 출력값(y)이 얼마나 변하는지를 계산해요.
이 글에서는 미분과 비교하여 변분에 대한 주요 개념을 알아 보겠습니다.
1. 미분(differentiation)
미분에서 다루는 대상은 y=f(x)와 같은 함수입니다. 이 함수는 숫자 x를 입력받아 숫자 f(x)를 출력하죠.
그런데 만일 입력값 x가 아주 조금 변할 때, 출력값 y가 얼마나 변하는지의 비율, 즉 기울기 또는 순간변화율을 계산하는 것을 미분이라고 해요.
미분 기호는 다음과 같이 표기해요.
\tag{1}
\begin{align}
{{df(x)}\over{dx}}, ~~f^{\prime}(x)
\end{align}미분을 하는 이유중의 하나는 출력값 f(x)가 최대와 최소가 되는 지점 x를 구하기 위함이에요.
예를 들어 함수 f(x)=x^2이 있을 때 함수값 f(x)가 최소가 되기 위한 점 x를 찾기 위해서는 함수의 미분이 0을 만족하는 x를 찾으면 돼요.
\tag{2}
\begin{align}
f^{\prime}(x) = 2x =0
\end{align}즉, 위 조건을 만족하기 위해서는 x=0이 되어야 합니다. 실제로 f(x)=x^2의 최소값은 x=0에 존재합니다.
이와 동일한 방식으로 f(x)가 최대가 되는 지점의 x를 구하기 위해서도 미분을 사용합니다.
결론적으로 최소지점 또는 최대지점에서 x를 dx만큼 아주 조금 바꿔도, df(x)는 1차 근사에서 변하지 않는다는 뜻입니다.
2. 변분 (Variation)
변분에서 다루는 대상은 범함수(functional)입니다. 보통 J[y(x)]로 표기하는데요. 중요한 것은 범함수 J가 숫자가 아닌 함수를 입력으로 받는다는 것이 미분과의 중요한 차이에요.
변분법에서 중요하게 나오는 범함수는 ‘최소 경로(S)’로서 다음과 같이 표기됩니다. 이 범함수도 함수 y(x)를 입력으로 받아 숫자 S를 출력하게 됩니다.
\tag{3}
\begin{align}
S[y(x)] = \int_{x_1}^{x_2} F(y, y^{\prime}, x)dx
\end{align}변분이 하는 일은 함수 y(x)의 모양이 아주 조금 변할 때 출력값 S가 얼마나 변하는지를 계산하게 됩니다. 기호로 표기하면 변분은 \delta S라고 하죠.
범함수의 S가 최소가 되게 하는 최적의 함수 y(x)를 찾는 것은 중요한 문제 중의 하나입니다.
만약 y(x)가 범함수 S가 최소가 되게 하는 최적의 함수라면, 그 함수를 살짝 변형시켰을 때 범함수의 출력값 S는 1차 근사에서 변하지 않아야 합니다.
이것을 수학 기호로 표현한 것이 \delta S =0이고, 1차적으로 거의 변하지 않는다라고 말합니다. 그리고 이 조건을 만족하기 위해서는 (3)식의 F가 다음의 조건을 만족해야 해요.
\tag{4}
\begin{align}
{{\partial F}\over{\partial y}} - {{d}\over{dx}}\Big( {{\partial F}\over{\partial y^{\prime}}} \Big) =0
\end{align}(4)식을 오일러-라그랑주 방정식이라고 불러요. 이 방정식을 풀면 범함수 S가 최소값을 갖는 최적의 함수 y(x)를 구하게 됩니다.
3. 변분 vs. 미분
3-1. 개념 비교
변분과 미분을 표로 만들어 비교하면 다음과 같아요.
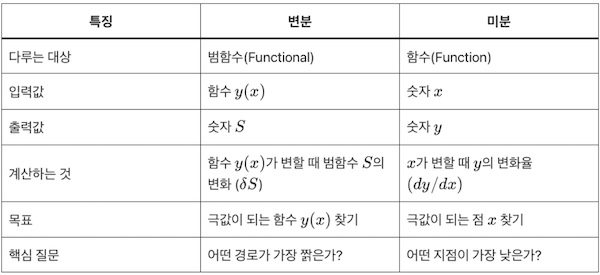
| 특징 | 변분 | 미분 |
|---|---|---|
| 다루는 대상 | 범함수(Functional) | 함수(Function) |
| 입력값 | 함수 y(x) | 숫자 x |
| 출력값 | 숫자 S | 숫자 y |
| 계산하는 것 | 함수 y(x)가 변할 때 범함수 S의 변화 (\delta S) | x가 변할 때 y의 변화율 (dy/dx) |
| 목표 | 극값이 되는 함수 y(x) 찾기 | 극값이 되는 점 x 찾기 |
| 핵심 질문 | 어떤 경로가 가장 짥은가? | 어떤 지점이 가장 낮은가? |
3-2. 연산규칙 비교
미분에서 쓰던 공식을 변분에서도 그대로 사용하면 됩니다.
| 연산법칙 | 변분 | 미분 |
|---|---|---|
| 기본 꼴 | \delta(y^2) = 2y \delta y | d(y^2) = 2y dy |
| 합의 법칙 | \delta(f+g) = \delta f + \delta g | d(f+g) = d f + dg |
| 곱의 법칙 | \delta(fg)=f\delta g + g \delta f | d(fg)=fdg + g df |
| 연쇄 규칙 | \delta(F(y))=F^{\prime} \delta y | d(F(y))=F^{\prime} dy |
다만, 미분은 x가 변하면서 f(x)도 변하는 것을 다루지만, 변분은 x를 고정시킨 상태에서, 즉 \delta x =0인 상태에서 함수 y(x)를 변화시켜 범함수 S가 달라지는 것을 다룹니다.
이에 따라 중요한 성질이 발생하는데요. 바로 미분과 변분의 순서를 서로 바꿔도 된다는 거에요.
\tag{5}
\begin{align}
\delta \Big({{dy}\over{dx}}\Big) = {{d}\over{dx}}(\delta y)
\end{align}\tag{6}
\delta y^{\prime} = (\delta y)^{\prime}이 성질 덕분에 오일러-라그랑주 방정식을 유도할 때 부분적분을 할 수 있게 됩니다.