ilovemyage
내 나이의 빛깔
전체 글 목록
체계적으로 분류된 전체 글 목록을 보고 싶으면 아래 사진을 클릭하세요.
최신 글
시간날 때마다 다양한 글을 계속 작성하고 있습니다.
- 간섭 무늬 : Young의 간섭 실험
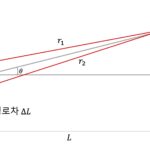
 Last Updated on 2025-12-27 by BallPen Young의 이중 슬릿 실험을 통해 간섭 무늬 생성 조건을 알아 봐요. 간섭 무늬 생성 원리를 이해하면 빛이 파동성을 갖는다는 성질을 이해할 수 있습니다. 고전적인 입장에서 빛이 만일 입자라면 서로 … Read more
Last Updated on 2025-12-27 by BallPen Young의 이중 슬릿 실험을 통해 간섭 무늬 생성 조건을 알아 봐요. 간섭 무늬 생성 원리를 이해하면 빛이 파동성을 갖는다는 성질을 이해할 수 있습니다. 고전적인 입장에서 빛이 만일 입자라면 서로 … Read more - 기체 분자 운동론에서의 온도
 Last Updated on 2025-12-16 by BallPen 기체 분자 운동론의 관점에서 기체의 온도를 생각해 봐요. 기체 분자 운동론에서의 온도 정의를 알아봐요. 결론부터 말씀드리면 기체 분자의 온도란 기체 분자의 평균 병진운동에너지와 직접적인 관련을 가져요. 따라서 기체의 온도가 … Read more
Last Updated on 2025-12-16 by BallPen 기체 분자 운동론의 관점에서 기체의 온도를 생각해 봐요. 기체 분자 운동론에서의 온도 정의를 알아봐요. 결론부터 말씀드리면 기체 분자의 온도란 기체 분자의 평균 병진운동에너지와 직접적인 관련을 가져요. 따라서 기체의 온도가 … Read more - 기체 분자 운동론에서의 압력
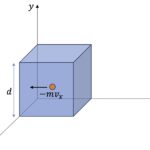
 Last Updated on 2025-12-14 by BallPen 미시적 이상 기체 운동론 관점에서 기체의 압력이 어떻게 설명되는지 알아 봐요. 기체분자 운동론에서의 압력(pressure)이란 미시적 이상 기체 분자 운동론 관점에서 압력을 설명하는 개념이에요. 부피가 인 용기에 이상 기체 분자가 … Read more
Last Updated on 2025-12-14 by BallPen 미시적 이상 기체 운동론 관점에서 기체의 압력이 어떻게 설명되는지 알아 봐요. 기체분자 운동론에서의 압력(pressure)이란 미시적 이상 기체 분자 운동론 관점에서 압력을 설명하는 개념이에요. 부피가 인 용기에 이상 기체 분자가 … Read more - 변분(variation)
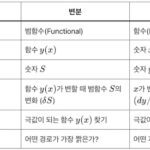
 Last Updated on 2025-12-09 by BallPen 변분의 개념을 알아보고 미분과의 차이점을 이해해 봐요. 변분(variation)이란 함수의 모양이 아주 조금씩 변할 때(), 출력값()가 얼마나 변하는지()를 계산하는 것을 말합니다. 반면에 미분이란 입력값()이 아주 조금씩 변할 때, 출력값()이 얼마나 … Read more
Last Updated on 2025-12-09 by BallPen 변분의 개념을 알아보고 미분과의 차이점을 이해해 봐요. 변분(variation)이란 함수의 모양이 아주 조금씩 변할 때(), 출력값()가 얼마나 변하는지()를 계산하는 것을 말합니다. 반면에 미분이란 입력값()이 아주 조금씩 변할 때, 출력값()이 얼마나 … Read more - scp 명령어 활용 방법
 Last Updated on 2025-12-28 by BallPen scp 명령어로 파일 전송하는 요령을 알아 봐요. scp 명령어(scp command)를 사용하면 원격서버로부터 로컬로 파일을 다운받거나 원격서버로 파일을 업로드할 수 있어요. 의외로 많이 사용하는 명령어 입니다. 1. 서버로부터 로컬로 파일 … Read more
Last Updated on 2025-12-28 by BallPen scp 명령어로 파일 전송하는 요령을 알아 봐요. scp 명령어(scp command)를 사용하면 원격서버로부터 로컬로 파일을 다운받거나 원격서버로 파일을 업로드할 수 있어요. 의외로 많이 사용하는 명령어 입니다. 1. 서버로부터 로컬로 파일 … Read more