BallPen

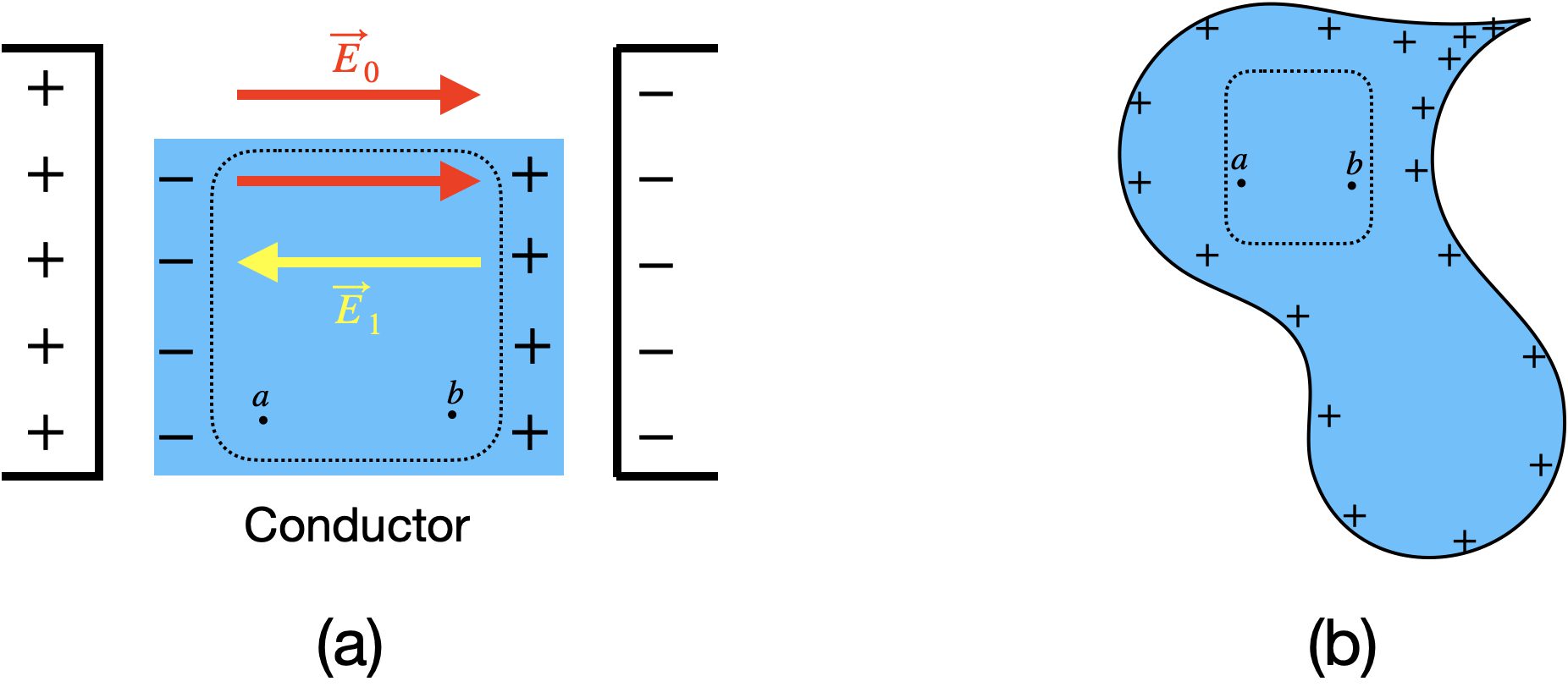
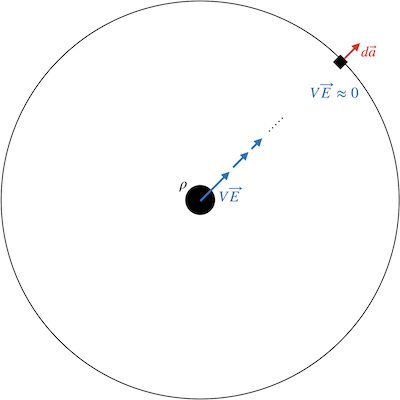
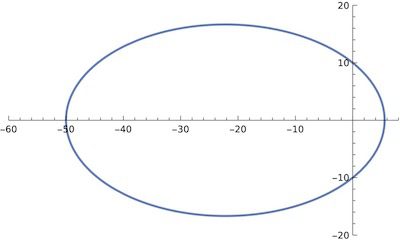
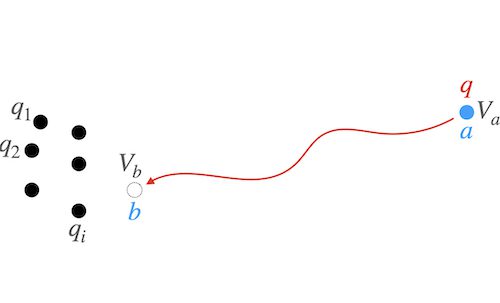
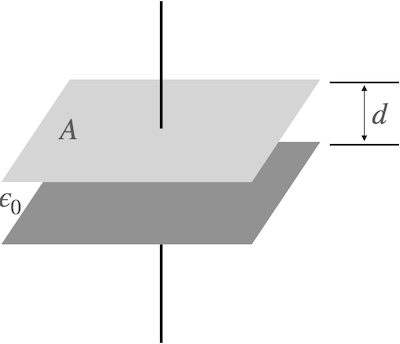
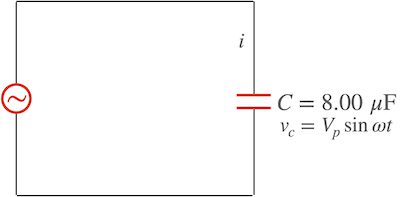
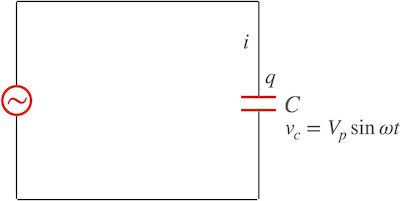
도체가 갖는 기본적인 성질을 알아봐요. 도체 기본 성질 몇가지를 함께 알아 봐요. 전자기학 관점에서 도체는 재미있는 성질들이 있는데요. 결론부터 말씀드리면 다음과 같습니다. 그럼 하나 하나 구체적으로 알아봐요. 아래는 이번 글의 목차입니다. 이 글에서 사용된 그림 자료는 아래에서 다운 받을 수 있습니다. 맥의 키노트로 작성되었어요. 맥 키노트 파일: conductor_basic_properties.key Contents1. 도체 기본 성질1-1. 도체속에서 전기장은 0이다.[외부 … Read more

전하가 연속적으로 분포된 공간의 에너지는 얼마나 될까요? 연속 전하 분포의 에너지 공식이 어떻게 표현되는지를 이번 글에서 함께 알아봐요. 지난 글에서 전하들이 띄엄 띄엄 모여진 점전하 분포의 에너지에 대해 알아봤는데요. 그 점전하 분포들이 연속적으로 분포된 경우를 연속 전하 분포라고 해요. 결론부터 말씀드리면 무한대 크기의 공간에서 연속 전하 분포에 저장된 에너지는 다음과 같이 주어집니다. 그리고 위 공식을 … Read more

이심률에 따른 궤도의 모양을 알아봐요. 궤도 이심률(orbital eccentricity)이란 행성의 궤도모양을 결정하는 값을 말합니다. 중력이 작용하는 상황에서 궤도 방정식을 만든 후 그 방정식을 풀면 회전각도 의 함수로서 원점으로부터 행성까지의 거리 를 도출할 수 있어요. 결과 식의 모양은 다음과 같아요. 여기서 는 상수이고, 은 이심률이라 불리는 값으로, 이 값에 따라 궤도 모양이 달라집니다. 결론부터 말씀드리면 이심률 값에 … Read more

점전하 분포에 저장된 에너지를 구해 봐요. 점전하 분포의 에너지 계산 방법을 소개합니다. 결론부터 말씀드리면 한 개의 전하 를 전위차 를 극복하며 이동시키기 위해 필요한 일 는 다음과 같이 주어집니다. 그리고 여러개의 전하 를 순차적으로 하나씩 이동시킬 때 필요한 일, 또는 그로 인해 생성된 점전하 분포에 저장된 전체 에너지는 다음과 같습니다. 여기서 재미있는 것은 위 두 … Read more

회로에서 저항기의 역할과 저항기들이 직렬과 병렬연결되었을 때 합성 저항을 어떻게 구하는지 알아봐요. 저항기(resistor)란 저항의 성질을 갖는 전자 부품을 말합니다. 그래서 저항기의 저항이 클 수록 회로에 흐르는 전류는 작아지고, 저항이 작을 수록 전류는 커집니다. 저항기들은 회로에서 직렬 또는 병렬연결될 수 있는데요. 그때 등가 합성 저항 구하는 방법을 알아볼거에요. 결론부터 말씀드리면 저항기 , , 가 직렬연결되었거나 병렬연결되면 … Read more

전기용량 리액턴스와 유도 리액턴스를 구하는 예제입니다. 리액턴스 예제 풀이입니다. 아래는 이번 글의 목차에요. 이 글에 사용된 그림 파일 원본은 아래에서 다운 받으세요. 키노트 파일이 원본이고 파워포인트 파일은 키노트 파일을 변환한거라 일부 호환성 문제가 있을 수 있어요. 편집해서 사용하시기 바랍니다. 맥 키노트 파일: reactance_examples.key 파워포인트 파일: reactance_examples.pptx Contents1. 전기용량 리액턴스 예제[문제][풀이]2. 유도 리액턴스 예제[문제][풀이] 1. 전기용량 … Read more