Last Updated on 2023-01-01 by BallPen
벡터끼리 곱하는 한 방법으로 내적이 있습니다. 내적을 하면 그 결과 값은 스칼라가 됩니다.
벡터와 벡터를 곱하는 방법에는 내적 및 외적이 있습니다.
그중에서 내적은 벡터끼리 곱하면 그 결과가 스칼라가 나오는 계산법인데요. 그래서 내적을 다른 말로 ‘스칼라곱‘이라고도 부릅니다.
이번 글은 내적, 즉 스칼라곱의 기하학적 의미, 계산 방법, 활용 사례를 알아봅니다. 혹시 벡터의 덧셈 및 벡터의 뺄셈 등의 내용이 궁금하면 이전 글을 참조해 주세요.
아래는 이번 글의 목차입니다.
1. 곱셈을 하는 방법의 종류
1-1. 실수와 실수의 곱 (스칼라와 스칼라의 곱)
일반적으로 두 숫자 c_1=23.0과 c_2 = 21.5를 곱한다고 하면 아래 (1)식과 같이 스칼라끼리 곱하는 방법이 있습니다.
\tag{1}
\begin{align}
c_1 c_2 &= c_1 \cdot c_2 = c_1 \times c_2\\
&=23.0 \times 21.5 \\
&= 495
\end{align}가장 보편적인 계산 방법이죠. 이때 곱해지는 두 숫자 사이에는 (1)식의 첫번째 줄과 같이 곱셈기호를 생략해도 되고, 가운데 점을 찍어도 되고, \times기호를 사용해도 됩니다.
그런데 물리량에는 스칼라량만 있는 것이 아니고 크기와 방향을 갖는 벡터량도 있습니다. 그렇다면 벡터량의 곱은 어떻게 표현할 수 있을까요.
벡터가 곱해지는 경우에는 총 3가지가 있습니다. 하나씩 알아보죠.
1-2. 벡터의 실수배 (벡터와 스칼라의 곱)
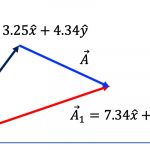
첫번째는 벡터에 스칼라인 실수를 곱하는 것입니다. 벡터 \vec A = 2.32 \vec x + 3.11 \vec y에 스칼라 c=7.10이 곱해지는 경우 아래 (2)식과 같이 계산하면 됩니다.
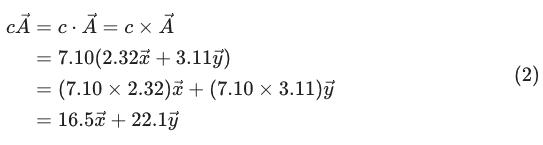
이때 곱해지는 스칼라와 벡터 사이에는 (2)식의 첫번째 줄과 같이 곱셈기호를 생략해도 되고, 가운데 점을 찍어도 되고, \times기호를 사용해도 됩니다.
아울러 벡터에 스칼라를 곱하면 벡터 방향은 그대로 유지되나 크기는 스칼라의 배수만큼 더 커지게 됩니다. 아래 [그림 1]과 같이요.
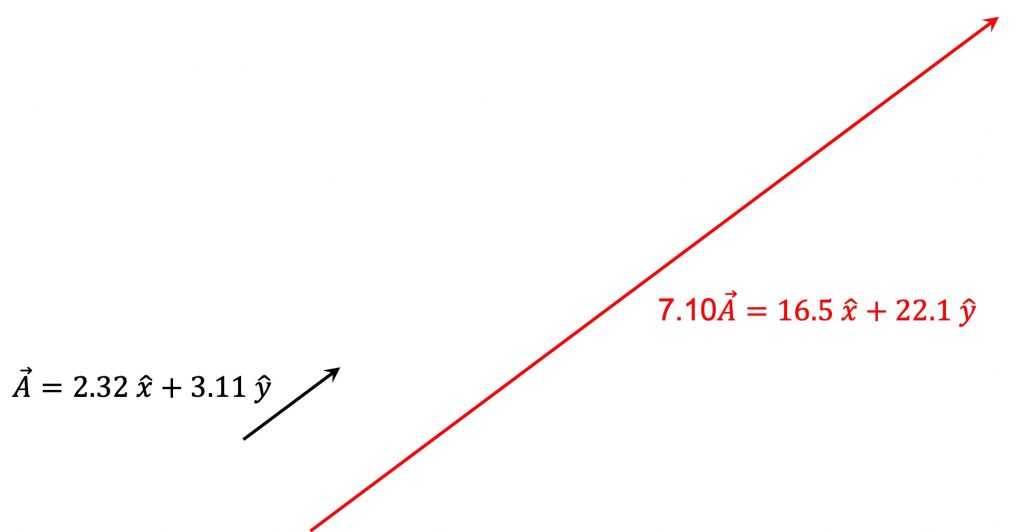
1-3. 내적 (벡터와 벡터의 곱, 결과는 스칼라)
두번째는 벡터와 벡터를 곱하는 내적입니다. 이것이 이번 글의 내용이므로 구체적 의미와 방법은 아래에 계속 기술하겠습니다.
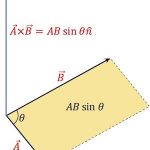
1-4. 외적 (벡터와 벡터의 곱, 결과는 벡터)
마지막으로 벡터와 벡터를 곱하는 외적이 있습니다. 이에 대해서는 다른 글로 다루겠습니다.
이제부터 내적에 대해 구체적으로 알아봐요.
2. 내적
2-1. 기하학적 의미
위에서 말씀드렸듯이 내적이란 벡터와 벡터를 곱하는 방법의 한 종류입니다.
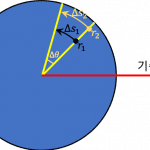
내적은 한 벡터에 다른 벡터를 투영한 후 그 크기를 곱하게 됩니다. 말이 상당히 어려워 보이지만 아래의 그림 [2]를 보시면 이해하기 쉽습니다.
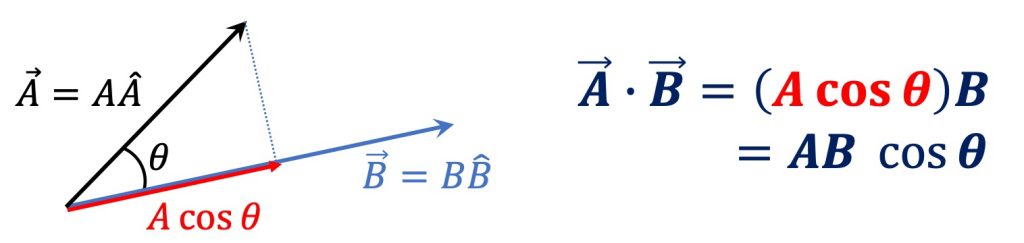
벡터 \vec A와 \vec B가 있는데요. 두 벡터가 사이각 \theta를 이루고 있다고 생각해봐요.
이때 벡터 \vec A를 벡터 \vec B에 투영한 것이 빨강색 화살표가 되는데요. 투영이라 함은 벡터 \vec B의 화살 위쪽에 조명이 있을 때 이 조명에 의해 벡터 \vec A의 그림자가 벡터 \vec B에 만들어지는 것을 말합니다.
그렇다면 투영된 빨강색 화살표의 크기는 A \cos \theta가 될 것입니다. 이 값을 벡터 \vec B의 크기와 곱하는 방법이 내적이에요.
수식으로 표현하면 아래 (3)식과 같습니다.
\tag{3}
\begin{align}
\vec A \cdot \vec B &= (A \cos \theta)B\\
&=AB\cos \theta
\end{align}여기서 굳이 벡터끼리의 곱 연산을 (3)식과 같이 해야하는 이유가 궁금할 수 있어요. 그것은 자연계에서 벌어지는 여러 현상이 (3)식의 내적 계산 방법을 적용하면 명확히 설명되기 때문이에요.
당장은 낮설 수 있지만 나중에 아래쪽 활용 사례를 보면 이해할 수 있습니다.
아울러 (3)식에 따르면 \vec A와 \vec B를 곱할 때 가운데 점 \cdot을 찍었어요. 그 가운데 점을 내적 기호 라고 합니다.
두 벡터를 내적하고자 한다면 내적 기호를 반드시 붙여주어야 해요. 곱셈이니까 가운데 점을 빼거나 \times로 바꾸어도 될거라고 생각하면 절대 안됩니다. 완전히 다른 계산을 하거나 계산을 못하게 되 버려요.
또한 (3)식에서와 같이 두 벡터의 내적은 스칼라가 됩니다. 왜냐면 A와 B는 두 벡터의 크기이고 \cos \theta도 크기만 있는 양이기 때문입니다.
그래서 두 벡터를 내적하면 결과가 스칼라가 된다고 말하는 것입니다.
2-2. 수학적 계산 방법
성분법으로 표기된 두 벡터를 수학적으로 내적하는 방법입니다. 기본적으로 (3)식의 내적의 정의를 그대로 사용하니 어렵지 않아요.
벡터 \vec A = A_x \hat x + A_y \hat y와 벡터 \vec B = B_x \hat x + B_y \hat y를 내적해보겠습니다.
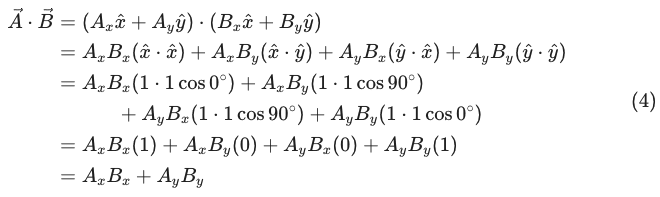
(4)식에서 두번째 줄의 괄호는 단위벡터끼리의 내적이므로 (3)식의 정의를 적용한 것이 세번째 줄이 되겠습니다.
이때 각 단위벡터의 크기는 1이고, 동일 방향의 단위벡터끼리 내적하면 사이각이 0도 이므로 \cos 0^\circ = 1이 되고 수직한 단위벡터끼리 내적하면 사이각이 90도이므로 \cos 90^\circ = 0 이 된 것입니다.
또한 (4)식의 마지막 줄에서와 같이 두 벡터를 내적한다는 의미는 두 벡터의 동일방향의 크기 성분끼리 곱하고 모두 더하여 단일의 스칼라 값이 도출되는 것으로 이해하시면 됩니다.
3. 내적 예제 풀이
(예제) 벡터 \vec {A} = 1 \hat{x} + 1 \hat{y} + 1 \hat{z}와 \vec {B} = 1 \hat{x} + 1 \hat{y} + 0 \hat{z}가 있다. 이때 두 벡터 사이의 각도는 35.26 ^\circ이다. 이 두 벡터에 대한 (3)식과 (4)식을 이용한 내적의 결과가 같음을 보여라.
(풀이) (3)식과 (4)식을 이용해 각각의 내적 값을 구하고 비교합니다.
우선 (3)식을 이용해 내적하기 위해서는 두 벡터의 크기인 A와 B를 구해야 합니다.(참고로 벡터 크기 기호는 |\vec{A}|와 |\vec{B}|의 형태로도 표기하기도 합니다.)
\tag{5}
\begin{align}
A &=\sqrt{{A_x}^2 + {A_y}^2 + {A_z}^2}\\
&=\sqrt{1^2 + 1^2 + 1^2}\\
&=\sqrt{3}
\end{align}\tag{6}
\begin{align}
B &=\sqrt{{B_x}^2 + {B_y}^2 + {B_z}^2}\\
&=\sqrt{1^2 + 1^2 + 0^2}\\
&=\sqrt{2}
\end{align}(3)식의 내적 정의를 그대로 사용하면 그 결과 값은 아래 (7)식과 같이 2.00이 나옵니다.
\tag{7}
\begin{align}
\vec{A} \cdot {\vec{B}} &= AB \cos \theta\\
&=\sqrt{3} \sqrt{2}{\cos 35.26 ^\circ}\\
&=2
\end{align}이번에는 (4)식을 기반으로 내적을 하면 아래 (8)식과 같습니다.
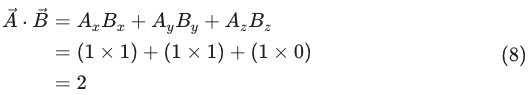
이상과 같이 (3)과 (4)식을 이용한 내적은 (7)과 (8)식의 결과와 같이 서로 동일합니다.
4. 내적의 성질
4-1. 교환법칙 성립
내적은 아래의 (9)식과 같이 교환법칙이 성립합니다. 즉 두 벡터의 곱의 순서를 바꾸어도 결과는 동일합니다.
그 이유는 아래 (9)식의 좌변이 AB \cos \theta인 것이나 우변이 BA \cos \theta인 것이나 수학적으로 같기 때문입니다.
\tag{9}
\vec{A} \cdot \vec{B} = \vec{B} \cdot \vec{A}4-2. 분배법칙 성립
다음의 내적에 대한 분배법칙도 성립합니다.
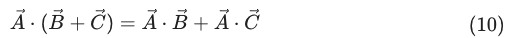
4-3. 스칼라와의 결합법칙 성립
k를 스칼라인 실수값이라고 했을 때 내적과의 결합법칙이 성립합니다.
\tag{11}
(k \vec A) \cdot \vec B = k(\vec A \cdot \vec B) = \vec A \cdot (k \vec B)4-3. 두 벡터가 수직하면 내적한 값은 0
두 벡터를 내적한 결과 값이 0이 나오면 두 벡터는 서로 수직합니다. 그 이유는 두 벡터의 사이각이 90^\circ이므로 (3)식에서 \cos 90^\circ는 0이 되기 때문입니다.
4-4. 두 벡터가 평행하면 내적한 값은 최대
두 벡터를 내적한 결과 값이 최대가 되기 위해서는 두 벡터가 평행해야 합니다. 그 이유는 두 벡터의 사이각이 0^\circ가 되면 (3)식에서 \cos 0^\circ는 1이 되기 때문입니다.
5. 내적의 활용 사례 (내적을 하는 이유)
5-1. 힘이 한 일
두 벡터를 내적해야 하는 대표적 용도는 힘이 한 일을 구할 때 입니다.
아래 [그림 3]과 같이 마찰이 없는 바닥에 물체가 놓여 있습니다. 이 물체에 일정한 힘 \vec F가 작용하여 물체를 변위 \vec d만큼 움직였다고 생각해보세요.
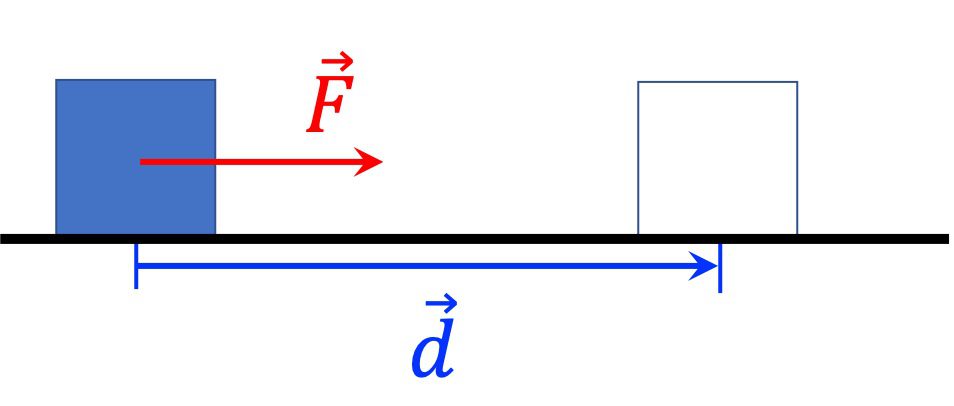
이때 힘 \vec F가 물체에 한 일 W는 물리학에서 다음과 같이 정의합니다.
\tag{12}
\begin{align}
W=Fd
\end{align}여기서 F는 힘 벡터 \vec F의 크기이고 d는 변위 벡터 \vec d의 크기입니다.
그렇다면 (12)식은 힘벡터와 변위벡터가 주어진 어느 경우에나 성립할까요? 그렇지 않습니다.
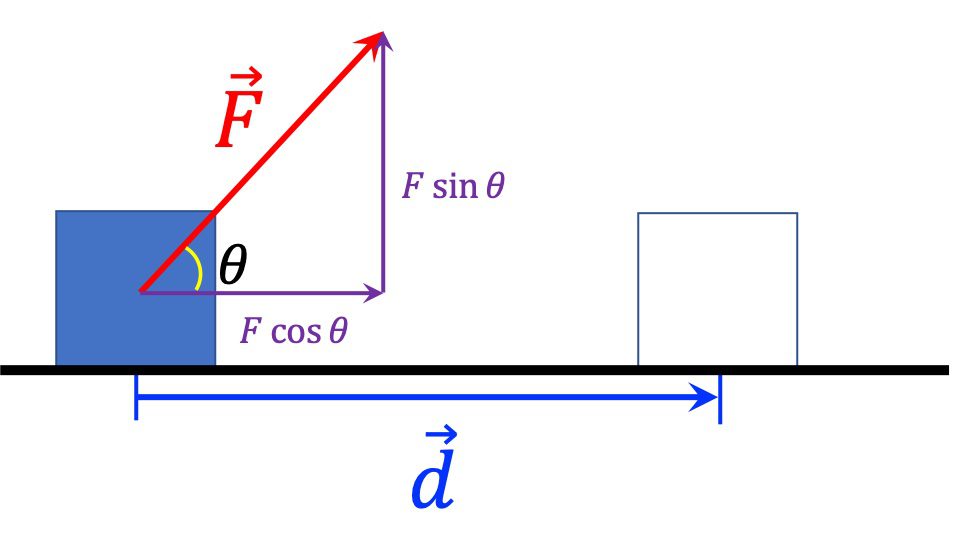
위에 있는 [그림 4]는 힘 벡터와 변위벡터가 [그림 3]과 같이 서로 평행하지 않습니다. 그림과 같이 힘 벡터 \vec F 은 변위 벡터 \vec d 의 방향과 \theta만큼 어긋나 있습니다.
그러면 물체를 d만큼 이동시키는데 한 힘은 \vec F의 수평성분이 담당합니다. 이 힘의 크기는 [그림 4]에 표기한바와 같이 F \cos \theta로 주어집니다.
결국 이 경우 물체에 한 일 W는 다음과 같이 주어집니다.
\tag{13}
\begin{align}
W&=(F \cos \theta ) d\\
&=F d \cos \theta
\end{align}이러한 결과는 힘 \vec F가 물체에 가해져 물체가 변위 \vec d만큼 이동했을 때 힘이 한 일은 (12)식처럼 주어질때도 있고 (13)식처럼 주어질 때도 있다는 것을 말합니다.
이 차이는 두 벡터 사이의 사이각 때문에 생기는 것으로 두 벡터가 평행하면 (12)식처럼, 두 벡터가 평행하지 않으면 (13)식처럼 표현해야 하는 것이죠.
5-2. 내적을 이용한 힘이 한 일의 표현
이렇게 되면 힘이 한 일을 구할 때 변위와의 사이각 유무에 따라 공식이 다른 것으로 생각할 수 있는데요. 그렇지는 않습니다. 왜냐면 (12)식과 (13)식을 아우르는 단일의 표현식이 있어요. 그것은 바로 아래 (14)식처럼 내적을 이용해 표현하면 됩니다.
\tag{14}
W=\vec F \cdot \vec d(14)식과 같이 힘이 한 일을 내적으로 표현하면 \vec F와 \vec d의 사이각이 평행하면 \cos 0^\circ = 1이 되어 (12)식으로 귀결됩니다. 또한 두 벡터의 사이각 \theta가 존재하면 (13)식으로 귀결되는 것이죠.
정리하면 어느 물체에 힘이 한 일에 대한 아주 일반적이고 간결한 식은 내적을 이용하여 표현한 (14)식이 되겠습니다.
의외로 내적을 사용해야 하는 경우가 물리학에서 많답니다.

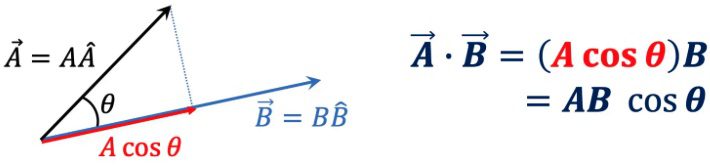



8 thoughts on “내적 – 벡터끼리 곱하여 스칼라가 되는 계산법”