Last Updated on 2021-12-29 by BallPen
실험실에서 사용되는 원심분리기의 원리와 RPM, RCF, G-force 값 사이의 차이를 알아 보겠습니다.
원심분리기 원리에 대해 최근 누군가가 질문하여 공부할 기회가 있었어요.
그리고 이 과정에서 원심분리기의 RPM, RCF, G-force 값의 개념이 활용된다는 것을 알았습니다. 그래서 이 개념들의 정의와 관련 공식을 유도해보았어요.
아래는 이번 글의 목차입니다.
Contents
혹시 RCF관련 공식으로 바로 이동하고 싶은 사람은 목차에서 ‘4. 원심분리기 RCF와 G값’을 클릭하세요.
1. 중력가속도와 구심가속도
원심분리기의 동작 원리를 이해하기 위해서는 중력가속도와 구심가속도를 우선 알아야 합니다.
1-1. 중력가속도
질량을 갖는 물체가 높은 곳에서 떨어지면 속도가 점점 증가하죠. 이러한 현상을 우리는 물체가 가속도를 갖고 운동한다고 말합니다.
가속도는 다음 (1)식과 같이 정의됩니다.
\tag{1}
\begin{align}
a &= {{\Delta v} \over {\Delta t}}\\
&={{v_2 - v_1}\over{ t_2 - t_1}}
\end{align}(1)식에서 t_2는 나중시간이고 t_1은 처음시간입니다. 그러므로 (1)식의 분모는 경과시간을 뜻합니다.
또한 v_2는 나중시간에서의 속력이고 v_1은 처음시간에서의 속력입니다. 그러므로 (1)식의 분자는 속력의 변화량을 뜻합니다.
결국 가속도란 단위 경과시간당 속력이 변화한 량을 뜻합니다.
그런데 지구 표면에서 물체를 떨어뜨리면 질량과 무관하게 일정한 가속도 값을 갖는다는 것이 실험적으로 알려져 있어요. 그 가속도 값을 구해보면 크기가 9.8 ~\mathrm{m/s^2}이고 지구 중심방향을 향합니다.
따라서 일반적인 가속도의 기호 a를 사용하지 않고 특별히 g라는 기호를 사용하여 아래 (2)식과 같이 중력가속도를 구분하여 정의합니다.
\tag{2}
g= 9.8 ~\mathrm{m/s^2}그렇다면 물체가 가속도를 갖는 이유는 무엇일까요? 바로 뉴턴운동의 제2법칙으로 설명됩니다.
\tag{3}
F_g=mg중력장내에서 질량 m인 물체에 힘 F가 작용하면 물체의 중력가속도 g가 나타나게 되는 것이죠.
1-2. 구심가속도
질량 m인 물체가 원형의 궤도를 따라 회전하기 위해서는 원궤도의 중심 방향을 향하는 구심력이 필요합니다.
만일 실과 연결된 어느 물체를 손으로 머리 위에서 회전 시키고 있다고 생각해보세요. 이때 회전하는 물체를 중심방향으로 당겨야 회전운동이 일어납니다. 반대로 물체를 회전시키다가 잡고 있던 실을 놓으면 물체는 회전운동을 하지 못하고 멀리 날아가 버립니다.
여기서 손으로 물체의 회전 중심방향을 향해 당기는 힘이 구심력이에요.
회전하는 물체에 구심력이 작용하면 (3)식에서와 같이 가속도 a가 존재해야 합니다.
아래의 [그림 1]을 보아주세요. 원궤도의 중심 O로부터 반지름 r인 궤도를 질량 m인 물체가 돌고 있어요.
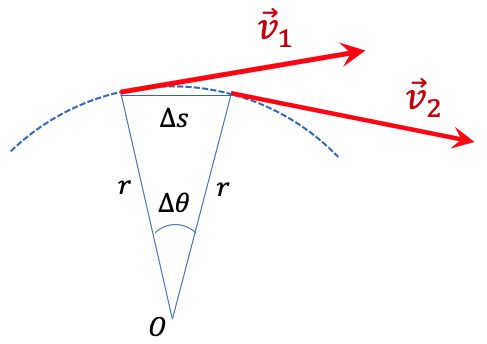
어느 처음시간에 물체의 속도 벡터가 v_1이고 나중시간에 물체의 속도 벡터가 v_2에요. 입자가 일정한 빠르기로 등속 원운동 한다고 가정하면 v_1과 v_2 벡터의 크기는 동일하지만 방향은 원 궤도의 접선방향으로 서로 다르게 됩니다.
속도 벡터의 크기가 동일하므로 속도의 변화량이 0일까요? 아니요 그렇지 않습니다. 크기가 동일할지라도 방향이 다르면 서로 다른 벡터입니다. 즉 두 벡터사이에는 속도의 변화량이 존재하게 됩니다.
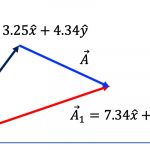
구체적으로 이해하기 위해서는 아래의 [그림 2]를 보아주세요.
![[그림 2] 속도의 변화량은 두 벡터 <span class="katex-eq" data-katex-display="false">v_1</span>과 <span class="katex-eq" data-katex-display="false">v_2</span>의 뺄셈을 통해 구할 수 있습니다.](https://ballpen.blog/wp-content/uploads/2021/12/Screen-Shot-2021-12-26-at-9.03.45-PM.jpg)
[그림 1]에서 빨강색으로 표시한 두 속도 벡터의 뺄셈 연산을 하면 속도의 변화량 \Delta v를 구할 수 있는데 그것을 검정색 화살표를 표기했어요.
벡터의 뺄셈 연산한 크기가 0이 아니라는 것은 변화량이 존재한다는 의미입니다. 아울러 검정색 화살표의 방향은 \Delta t가 매우 짧은 경우 원궤도의 중심을 향하게 됩니다.
수식 유도
[그림 1]과 [그림 2]에서 보여지는 두 삼각형으로부터 아래 (4)식의 관계가 성립합니다. 이때 물체가 등속 원운동하므로 v_1과 v_2의 크기가 서로 같아 이 두 기호를 모두 v로 바꾸어 쓸수 있어요.
\tag{4}
\begin{align}
{{\Delta v}\over{v_1}} = {{\Delta v}\over{v}}= {{\Delta s}\over{r}}
\end{align}이 식을 \Delta v에 대해 풀면 다음 (5)식과 같습니다.
\tag{5}
\begin{align}
\Delta v = {{v}\over{r}} \Delta s
\end{align}이제 (5)식의 속도 변화량을 (1)식에 대입하면 구심가속도를 구할 수 있어요.
\tag{6}
\begin{align}
a &= {{\Delta v} \over {\Delta t}}\\
&={{v}\over{r}}{{\Delta s}\over{\Delta t}}
\end{align}이때 \Delta t가 매우 작은 극한을 생각하면 \Delta s / \Delta t는 접선 속력 v의 순간값으로 수렴하게 됩니다.
따라서 (6)식의 가속도는 다음과 같이 정리할 수 있습니다.
\tag{7}
\begin{align}
a &= {{v^2}\over{r}}\\
&=r \omega^2 ~~(원궤도의 ~중심 ~방향)
\end{align}이 식에서 v는 v={{호의길이}\over{단위시간}}={{r \Delta \theta}\over{\Delta t}}=r \omega의 관계를 적용했어요.
정리하면 구심가속도는 물체가 반지름 r인 궤도를 각속력 \omega로 회전할 때 (7)식과 같이 주어집니다.
이때 중요한 것이 하나 있는데요. 회전하는 물체의 입장에서는 구심가속도를 일으키는 구심력을 느끼는 것이 아니라 원심력을 느끼게 됩니다. 원심력은 구심력과 크기는 갖고 방향은 원궤도의 바깥쪽을 향하는 가상력입니다.
결국 원심력에 의한 원심가속도의 크기는 (7)식과 동일하게 주어지지만 방향만 반대가 된다는 것을 명심하세요.
2. 원심분리기 용기에 작용하는 힘
원심분리기란 원심분리기용 용기내에 분리하고자 하는 혼합물을 넣고 고속으로 회전시키는 장치입니다. 그러면 물질의 밀도와 크기에 따라 혼합물내에 있는 물질들을 분리해낼 수 있게 되죠.
![[그림 3] 혼합물이 들어 있는 원심분리기 용기가 일정한 각속력 <span class="katex-eq" data-katex-display="false">\omega</span>로 회전하고 있습니다. 이 용액속에서 반지름 <span class="katex-eq" data-katex-display="false">r</span>의 궤도를 따라 질량 <span class="katex-eq" data-katex-display="false">m</span>인 입자도 회전하고 있어요.](https://ballpen.blog/wp-content/uploads/2021/12/Screen-Shot-2021-12-26-at-9.57.14-PM.jpg)
[그림 3]은 혼합물이 들어 있는 원심분리기용 용기가 일정한 각속력 \omega로 회전하고 있는 장면입니다.
이때 혼합물 내에는 질량 m인 입자가 존재하며 그 입자는 회전축으로부터 반지름 r인 곳에 있습니다.
그러면 이 입자에는 세개의 힘이 작용하게 됩니다.
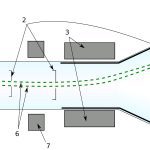
바로 원궤도의 바깥쪽을 향하는 원심력 \vec{F}_c, 유체속의 물체에 작용하는 부력 \vec{F}_b, 마지막으로 유체속에서 입자가 이동하는 동안 받게 되는 유체 저항력 \vec{F}_r 입니다.
![[그림 4] 질량 <span class="katex-eq" data-katex-display="false">m</span>인 입자가 들어 있는 혼합 용액이 원심분리기 용기에 들어 있습니다. 원심분리기가 동작되면 입자에는 원심력 <span class="katex-eq" data-katex-display="false">\vec{F}_c</span>, 부력 <span class="katex-eq" data-katex-display="false">\vec{F}_b</span>, 유체저항력 <span class="katex-eq" data-katex-display="false">\vec{F}_r</span>이 동시에 작용합니다.](https://ballpen.blog/wp-content/uploads/2021/12/Picture1.png)
물론 입자는 중력도 받습니다. 그러나 위에서 언급한 세 힘이 가로방향으로 작용하는 것에 비해 중력은 수직방향으로 작용하며, 원심분리기에 의해 제공되는 원심력에 비해 중력은 매우 작아 무시할 수 있습니다.
이제부터 입자에 작용하는 힘을 하나 하나 분석하여 용액속에서 입자의 이동 속력 v을 구해보겠습니다.
이 이동속력의 차이에 의해 혼합물 내에 들어있는 물질들을 서로 분리할 수 있게 되는 것이죠.
2-1. 원심력
원심분리기가 동작하면 [그림 3]과 같이 원심분리기 용기가 각속력 \omega로 회전합니다. 그리고 원심분리기 용기내에 들어있는 질량 m인 입자도 이 각속력으로 회전하며 그때의 회전 반지름을 r이라 두겠습니다.
그러면 이 입자는 원심가속도를 갖게 됩니다. 그 크기는 (7)식과 같으며 방향은 중심으로부터 멀어지는 바깥 방향이 됩니다.
이 관계를 다시 쓰면 아래 (8)식과 같습니다.
\tag{8}
\begin{align}
a_c &= {{v^2}\over{r}}\\
&=r \omega^2 ~~(원궤도의 ~바깥 ~방향)
\end{align}원심가속도가 주어졌으니 이 물체는 아래 식과 같이 뉴턴운동의 제2법칙에 따라 원심력을 받습니다.
\tag{9}
\begin{align}
F_c=ma_c = mr\omega^2
\end{align}윗식에서 입자의 질량 m은 입자의 밀도 \rho_p와 부피 V의 관계를 통해 아래 (10)식과 같이 정리할 수 있습니다. 아울러 입자의 반지름은 r ^{\prime}, 지름은 D로 표기하겠습니다.
\tag{10}
\begin{align}
m &=\rho_{p}V\\
&=\rho_p \times {{4}\over{3}}\pi {r^\prime}^3\\
&=\rho_p \times {{4}\over{3}} \pi \big( {{D}\over{2}}\big)^3\\
&=\rho_p{{\pi D^3}\over{6}}
\end{align}결국 입자에 작용하는 원심력 F_c는 (10)식을 (9)식에 대입하면 됩니다.
\tag{11}
\begin{align}
F_c &= mr\omega^2\\
&=\Big( \rho_p {{\pi D^3}\over{6}} \Big)
r \omega^2\end{align}2-2. 부력
유체속에 있는 입자가 받는 부력은 입자가 밀어낸 유체의 무게와 같습니다. 이것을 식으로 쓰면 아래 (12)식과 같습니다.
\tag{12}
\begin{align}
F_b = m_{f} g
\end{align}위 식에서 m_f는 입자가 밀어낸 유체의 질량입니다. 그리고 g는 가속도인데요. 중력가속도가 아닌 (8)식의 원심가속도 a_c를 대입해야 합니다.
유체, 즉 용액의 밀도를 \rho_f라 하고, 입자의 부피를 V라 하면 (12)식은 아래와 같이 바꿀 수 있습니다. 이 과정은 (10)식과 (11)식의 관계와 유사하게 동일하게 이해하시면 됩니다.
\tag{13}
\begin{align}
F_b &= m_{f} a_c\\
&=\rho_f V a_c\\
&=\rho_f \times {{4}\over{3}} \pi {r ^\prime} ^3 \times r \omega^2\\
&=\rho_f \times {{4}\over{3}} \pi \Big({{D}\over{2}}
\Big)^3 \times r\omega^2\\
&=\rho_f {{\pi D^3}\over{6}}r\omega^2
\end{align}2-3. 저항력
유체에 의해 작용하는 저항력은 스토크스의 법칙(Stokes’ law)으로 설명됩니다. 유체속에 있는 입자의 속력과 반대방향으로 작용하는 마찰력의 개념으로 이해하시면 됩니다.
스토크스의 법칙은 아래 (14)식과 같습니다. 이때 \eta는 유체의 점성계수이고, r \prime은 입자의 반지름, D는 입자의 지름, v는 유체내에서 입자의 속력입니다.
\tag{14}
\begin{align}
F_r &= 6 \pi \eta r^\prime v\\
&=6 \pi \eta \Big({{D}\over{2}}\Big) v\\
&=3 \pi \eta Dv
\end{align}2-4. 유체내 입자의 이동 속도
지금까지 원심분리기가 동작될 때 혼합물 속 입자에 작용하는 세 개의 힘에 대해 각각 설명드렸습니다.
이제 이 힘들을 종합하여 유체내 입자의 이동 속도를 구해보겠습니다.
입자에 작용하는 힘은 벡터입니다. 그러므로 [그림 4]에서 주어진 세 힘에 대한 벡터의 방향 관계를 고려하고 (11),(13),(14)식을 종합하면 다음의 운동방정식을 만들 수 있습니다.
\tag{15}
\begin{align}
{F}_c &= F_b + F_r\\
\Big( \rho_p {{\pi D^3}\over{6}} \Big) r \omega^2&=\rho_f {{\pi D^3}\over{6}} r\omega^2 + 3 \pi \eta Dv
\end{align}윗 식을 v에 대해 정리합니다.
\tag{16}
\begin{align}
3 \pi \eta Dv &= \rho_p {{\pi D^3}\over{6}} r\omega^2 - \rho_f {{\pi D^3}\over{6}} r \omega^2\\
\end{align}\tag{17}
\begin{align}
v=({\rho_p - \rho_f}) {{D^2}\over{18 \eta}} r \omega^2
\end{align}바로 위 (17)식이 유체내 입자의 이동속력을 나타냅니다. 입자의 이동 속력은 입자와 유체의 밀도차이에 비례하는 것을 알 수 있습니다.
결국 원심분리기를 동작시키면 유체와 입자의 밀도차이에 따라 서로 다른 유동속력을 갖게되어 혼합물을 구성하는 물질들을 구분해 낼 수 있게 되는 것입니다.
3. 원심분리기 rpm 및 각속력
rpm (revolution per minute)이란 원심분리기의 회전자가 회전할 때 1분당 몇 바퀴를 회전하느냐를 나타내는 척도입니다. 단위는 ‘회전수/min’ 입니다.
예를 들어 3000 rpm이라면 1분당 3000번 회전한다는 의미가 되는 것이죠.
결국 rpm은 회전 빠르기의 척도로 볼 수 있는데요. 그러나 일반적으로 과학 분야에서 회전빠르기를 사용할 때 rpm 보다는 위에서 자주 언급한 각속력 \omega를 더 자주 사용합니다.
rpm과 각속력 \omega는 아래 식과 같이 서로 변환할 수 있어요.
\tag{18}
\begin{align}
\omega &= {{rpm \times 2 \pi~ \mathrm{rad}}\over{1 ~\mathrm{min}}}\\
&={{rpm \times2 \pi~ \mathrm{rad}}\over{60~\mathrm{s}}}\\
&={{rpm\times\pi}\over{30}}
\end{align}윗식에서 \omega의 단위는 rad/s 입니다.
(예제) 원심분리기의 회전자가 3000 rpm으로 회전한다면 각속력은 얼마인가?
(Sol) (18)식을 이용하여 각속력을 구하면 됩니다.
\tag{19}
\begin{align}
\omega &= {{rpm \times \pi}\over{30}}\\
&= {{3000 \times \pi}\over{30}}\\
&=314~\mathrm{rad/s}
\end{align}1초당 314 rad을 회전하는 빠르기입니다.
4. 원심분리기 RCF와 G값
RCF (Relative Centrifugal force)란 혼합물내에 있는 입자에 작용하는 중력과 원심력사이의 비율을 뜻합니다.
즉 입자에 작용하는 중력의 크기에 비해 원심분리기가 회전함으로써 입자에 가하는 원심력이 어느정도 되느냐의 척도인 것이죠.
RCF는 (9)식의 원심력을 (3)식의 중력으로 나누는 것으로 정의됩니다. 두 힘사이의 비율 개념이므로 단위는 없습니다.
구체적인 수식으로는 아래와 같이 표현할 수 있어요.
\tag{20}
\begin{align}
RCF &= {{F_c}\over{F_g}}\\
&={{mr\omega^2}\over{mg}}
\end{align}그런데 (20)식의 두번째 줄에서 분모와 분자에 있는 질량 m은 서로 약분될 수 있어요. 그러면 아래 (21)식과 같이 RCF가 표현될 수 있어요.
\tag{21}
\begin{align}
RCF={{r\omega^2}\over{g}}
\end{align}결국 RCF는 중력가속도 대비 원심가속도의 크기가 몇 배인가로 해석될 수 있게 됩니다.
아울러 (18)식을 (21)식에 대입하면 몇 rpm에서 입자에 작용하는 RCF가 얼마인지를 구할 수 있어요. 아래 (22)에 정리할게요.
\tag{22}
\begin{align}
RCF &= {{r\omega^2}\over{g}} \\
&= {r \times({rpm \times \pi/30)^2}\over{g}}\\
&=(1.12\times10^{-3}) \times r(\mathrm{m}) \times rpm^2
\end{align}그런데 위 (22)식에서 회전자의 회전 반지름 r의 단위가 m로 되어 있어요. 그렇지만 보통의 원심분리기는 수 cm의 회전자가 사용되므로 m 단위를 사용하는 것 보다는 cm 단위를 사용하는게 편할 거에요.
이를 반영해서 최종적으로 RCF를 구하는 식은 다음과 같습니다.
\tag{23}
\begin{align}
RCF=(1.12 \times 10^{-5}) \times r (\mathrm{cm}) \times rpm^2
\end{align}(예제) 3180 rpm으로 회전하는 원심분리기가 있다. 회전자의 회전 반지름이 11.0 cm라면 RCF 값은 얼마인가?
(Sol) 위에서 주어진 (23)식을 활용하면 됩니다.
\tag{24}
\begin{align}
RCF &= (1.12 \times 10^{-5}) \times r (\mathrm{cm}) \times rpm^2 \\
&=(1.12 \times 10^{-5}) \times 11.0 \times 3180^2 \\
&\approx1,245
\end{align}바로 1,245가 나옵니다.
이것이 뜻하는 것은 원심분리기에서 제공하는 원심가속도가 중력가속도보다 1,245배 크다는 이야기입니다. 또한 원심분리기에서 제공하는 원심력이 중력보다 1,245배 크다는 의미와 같습니다.
이것을 표기할 때에는 “RCF 값은 1245 입니다” 또는 “G-Force는 1,245 g입니다.”라고 하시면 됩니다.




1 thought on “원심분리기 원리와 RPM, RCF, G 값의 차이”