Last Updated on 2024-01-15 by BallPen
삼중곱이란 벡터 3개의 곱셈을 말합니다. 삼중곱에는 스칼라 삼중곱과 벡터 삼중곱이 있어요.
삼중곱(triple product)이란 3개의 벡터가 외적과 내적으로 연결되어 있는 벡터끼리의 곱셈을 말합니다.
이번 글에서는 몇가지 삼중곱에 대한 이야기를 하고자 합니다.
재미있어요. 함께해봐요.
아래는 이번 글의 목차입니다.
Contents
1. 삼중곱
앞에서 말씀드렸듯이 삼중곱은 벡터끼리의 곱셈인데요. 벡터 3개가 곱해지는 형태를 말합니다. 벡터끼리의 곱이므로 내적(스칼라곱) 또는 외적(벡터곱)으로 연결되어 있어요.
예를 들면 아래와 같은 벡터끼리의 곱셈을 말합니다.
\tag{1}
\vec A \cdot (\vec B \times C)\tag{2}
\vec A \times (\vec B \times \vec C)물론 내적과 외적을 알면 (1)식과 (2)식에 주어진 삼중곱을 계산할 수 있어요.
그런데 왜 삼중곱을 더 구체적으로 알아야 할까요?
첫번째 이유는 삼중곱을 보다 쉽게 계산하기 위해서이고요. 두번째는 삼중곱을 다른 항등관계로 바꾸어 필요할 때 적절히 사용하기 위해서에요. 마지막으로 세번째는 성립하는 삼중곱과 성립하지 않는 삼중곱이 있음을 이해하는 거에요.
우리가 내적을 스칼라곱이라 하고 외적을 벡터곱이라 하는 이유는, 내적을 하면 결과가 스칼라가 나오기 때문이고, 외적을 하면 결과가 벡터가 나오기 때문이에요.
이와 비슷하게 삼중곱에는 삼중 스칼라곱과 삼중 벡터곱이 있어요.
말그대로 삼중 스칼라곱은 삼중곱을 하면 스칼라가 나오기 때문이에요. 벡터 삼중곱은 그 결과가 벡터가 나오기 때문에 그렇게 불러요.
이제 하나씩 알아볼까요.
2. 스칼라 삼중곱 증명
스칼라 삼중곱은 다음의 형태를 갖는 삼중곱을 말해요.
\tag{3}
\bold{\vec A \cdot (\vec B \times \vec C)}이것을 우리가 알고 있는 내적와 외적의 계산법을 이용해 전개해 볼께요. 그러면 아주 복잡해 보이는 식으로 전개가 되는데, 반대로 이를 간결한 형태로 표현할 수 있다는 것을 알게 됩니다.
그러면 (3)식의 계산이 오히려 쉬워진답니다.
2-1. 스칼라 삼중곱 전개와 행렬 표현
천천히 전개를 해보죠.
만일 아래의 전개 방법이 잘 이해가 안되면 내적(스칼라곱)에 대한 이전 글과 외적(벡터곱)에 대한 이전 글을 꼭 읽고 오세요. 그러면 바로 눈으로 보아도 이해가 갈거에요.
\tag{4}
\begin{align}
\vec A \cdot (\vec B \times \vec C) &= (A_x \hat x + A_y \hat y + A_z \hat z)\cdot
\begin{vmatrix}
\hat x & \hat y & \hat z\\
B_x & B_y & B_z\\
C_x & C_y & C_z
\end{vmatrix}\\
&=(A_x \hat x + A_y \hat y + A_z \hat z)\cdot\\
&~~~~~~~~~~~~~\big[ (B_y C_z - B_z C_y) \hat x + (B_z C_x - B_x C_z)\hat y + (B_x C_y - B_y C_x) \hat z \big]\\
&=A_x (B_y C_z - B_z C_y) + A_y (B_z C_x - B_x C_z) + A_z (B_x C_y - B_y C_x)\\
&=(A_x B_y C_z - A_x B_z C_y) + (A_y B_z C_x -A_y B_x C_z) + (A_z B_x C_y - A_z B_y C_x)
\end{align}전개를 했더니 (4)식의 마지막 줄과 같이 상당히 복잡해 보이는 형태가 나왔어요. 그런데 보기에도 매우 복잡해 보이는데 이것을 외워서 실제 문제에 적용하기는 쉽지 않아요.
하지만 스칼라 삼중곱의 전개 결과를 잘 보면 아래 (5)식과 같이 간결한 형태로 표현할 수 있어요.
\tag{5}
\vec A \cdot (\vec B \times \vec C) =
\begin{vmatrix}
A_x & A_y & A_z\\
B_x & B_y & B_z\\
C_x & C_y & C_z\\
\end{vmatrix}(5)식의 행렬식을 눈으로 전개해보세요. 그러면 (4)식과 동일한 결과가 도출되는 것을 알 수 있습니다.
따라서 스칼라 삼중곱이 주어지면 (5)식의 행렬 형태로 바꾸어 전개하면 결과인 스칼라 값을 쉽게 도출할 수 있답니다.
2-2. 기하학적 의미
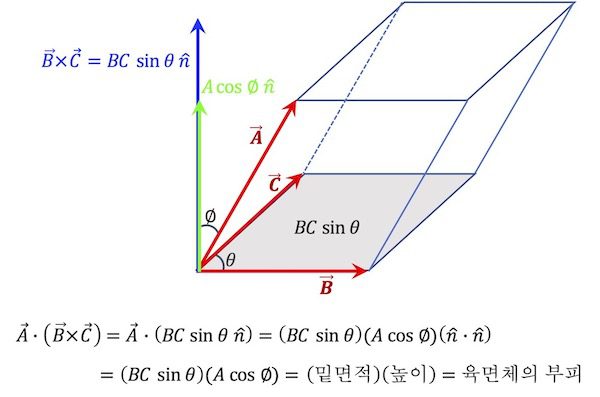
(3)식에 주어진 스칼라 삼중곱 \vec A \cdot (\vec B \times \vec C)은 기하학적으로 특별한 의미를 갖습니다. 아래 그림 [1]을 보아주세요.
![[그림 1] 스칼라 삼중곱. 스칼라 삼중곱은 기하학적으로 육면체의 밑면적과 높이의 곱을 의미합니다. 이것은 평행육면체의 부피가 되는 것이죠.](https://ballpen.blog/wp-content/uploads/2023/01/Picture1.jpg)
[그림 1]을 보면 평행육면체가 있어요. 그리고 세개의 벡터가 있는데요. 각 \vec A, \vec B, \vec C이에요.
여기서 (\vec B \times \vec C)의 크기는 육면체의 밑면적인 BC \sin \theta에 해당합니다. 그리고 방향은 그림에서 파랑색 화살표로 나타낸 것처럼 밑면적에 수직한 방향(기호로 \hat n)이 됩니다.
그리고 (\vec B \times \vec C)로 벡터 A를 내적하면 되는데요. (\vec B \times \vec C)에 벡터 \vec A를 투영하고, 그 크기 A \cos \phi와 (\vec B \times \vec C)의 크기 BC \sin \theta를 곱하면 됩니다.
지금까지 말한 것을 식으로 표현하면 아래와 같아요.
\tag{6}
\begin{align}
\vec A \cdot (\vec B \times \vec C) &= \vec A \cdot (BC \sin \theta \hat n) \\
&=(A \cos \phi ~\hat n)\cdot(BC \sin \theta ~\hat n) \\
&=(BC \sin \theta)(A \cos \phi) (\hat n \cdot \hat n)\\
&=(BC \sin \theta)(A\cos \phi)
\end{align}(6)식의 마지막 줄을 보면 BC \sin \theta는 [그림 1]에서 평행육면체의 밑면적과 같다는 것을 알 수 있어요. 그리고 A\cos \phi는 [그림 1]에서 육면체의 높이에 해당합니다.
결국 (6)식의 마지막 줄은 평행육면체의 밑면적과 높이를 곱하는 형태가 되는 것이죠.
결국 스칼라 삼중곱은 평행육면체의 부피 값과 같습니다.
\tag{7}
\vec A \cdot (\vec B \times \vec C) = 평행육면체의 ~~부피이 개념을 확대해 볼까요?
무슨 말이냐면 [그림 1]에 주어진 육면체의 부피는 밑면적과 높이만 곱하면 됩니다. 그러니까 밑면적을 (\vec C \times \vec A)의 크기로 잡아도 되고, (\vec A \times \vec B)의 크기로 잡아도 상관없어요.
결국 스칼라 삼중곱은 다음의 관계를 갖게 되요.
\tag{8}
\vec A \cdot (\vec B \times \vec C) = \vec B \cdot (\vec C \times \vec A) = \vec C \cdot(\vec A \times \vec B)\tag{9}
\begin{vmatrix}
A_x & A_y & A_z\\
B_x & B_y & B_z\\
C_x & C_y & C_z\\
\end{vmatrix}
= \begin{vmatrix}
B_x & B_y & B_z\\
C_x & C_y & C_z\\
A_x & A_y & A_z\\
\end{vmatrix}
= \begin{vmatrix}
C_x & C_y & C_z\\
A_x & A_y & A_z\\
B_x & B_y & B_z\\
\end{vmatrix}이상으로 스칼라 삼중곱을 알아봤어요. 다음에는 벡터 삼중곱을 알아봐요.
3. 벡터 삼중곱 증명
벡터 삼중곱은 아래와 같이 주어집니다.
\tag{10}
\bold{\vec A \times (\vec B \times \vec C)}이 벡터 삼중곱의 계산 결과는 벡터로 주어집니다. 그렇다면 정말 그렇게 되는지 (10)식도 한번 전개해 볼까요?
그러면 벡터 삼중곱을 다른 형태의 항등식으로 계산할 수 있는 관계가 얻어집니다. 이 관계를 백캡(BAC-CAB) 공식 이라고 불러요.
3-1. BAC-CAB 공식 (삼중곱 전개)
(10)식에서 (\vec B \times \vec C)는 이미 (4)식에서 전개를 해 놓은게 있습니다. 그 결과를 인용해서 활용하면 다음과 같아요.
\tag{11}
\begin{align}
\vec A \times (\vec B \times \vec C) &= \vec A \times \Big[(B_y C_z - B_z C_y) \hat x + (B_z C_x - B_x C_z)\hat y + (B_x C_y - B_y C_x) \hat z \Big]\\
&=
\begin{vmatrix}
\hat x & \hat y & \hat z\\
A_x & A_y & A_z\\
B_y C_z - B_z C_y & B_z C_x - B_x C_z & B_x C_y - B_y C_x
\end{vmatrix}\\
&=\Big( A_y(B_x C_y - B_y C_x ) -A_z(B_z C_x - B_x C_z)\Big)\hat x\\
&~~~~~~~~~~+\Big( A_z (B_y C_z - B_z C_y) - A_x (B_x C_y - B_y C_x)\Big) \hat y\\
&~~~~~~~~~~+\Big(A_x (B_z C_x - B_x C_z )-A_y(B_y C_z - B_z C_y)\Big) \hat z\\
&~~~~~~~~~~\color{blue}+\Big((Ax Bx Cx)\hat x + (A_y B_y C_y)\hat y + (A_zB_zC_z)\hat z \Big)\\
&~~~~~~~~~~~\color{red}-\Big((Ax Bx Cx)\hat x + (A_y B_y C_y)\hat y + (A_zB_zC_z)\hat z \Big)\\
\end{align}(11)식의 끝부분에 파랑색 수식과 빨강색 수식은 동일한 양을 더해주고 빼준거에요. 다소 복잡해 보이기는 하는데 연필을 잡고 천천히 정리해 보면 다음과 같습니다.
\tag{12}
\begin{align}
\vec A \times (\vec B \times \vec C) &= B_x(A_xC_x + A_yC_y + A_z C_z)\hat x +B_y(A_xC_x + A_yC_y + A_z C_z)\hat y\\
&~~~~~~~~~~~~~~~~~~~~~~~~~+B_z(A_xC_x + A_yC_y + A_z C_z)\hat x\\
&~~~~~-C_x(A_x B_x + A_y B_y + A_z B_z)\hat x - C_y(A_x B_x + A_y B_y + A_z B_z)\hat y\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~-C_z(A_x B_x + A_y B_y + A_zB_z)\\
\end{align}그리고 (12)식의 우변을 자세히 들여다 보면 다음의 백캡 공식이 성립하는 것을 알 수 있어요.
\tag{13}
\vec A \times (\vec B \times \vec C) = \vec B(\vec A \cdot \vec C) - \vec C(\vec A \cdot \vec B)3-2. 삼중 벡터곱의 비결합성
삼중 벡터곱은 결합법칙이 성립하지 않아요.
이게 무슨 말이냐면 아래 (14)식과 같이 좌변과 우변의 결과가 같지 않다는 거에요.
\tag{14}
\vec A \times (\vec B \times \vec C) \ne (\vec A \times \vec B)\times \vec C얼핏 보면 같기도 할 것 같은데 같지 않아요. 이에 대해 잠시 알아보겠습니다.
만약 (14)식과 달리 삼중 벡터곱의 결합법칙이 성립한다고 가정해 볼까요? 즉 좌변과 우변이 서로 같아요.
그러면 좌변에서 우변을 빼면 0이 되어야 할 거에요.
\tag{15}
\vec A \times (\vec B \times \vec C) - (\vec A \times \vec B)\times \vec C = 0이 식의 첫번째 항에 BAC-CAB 공식을 적용해봐요. 그리고 두번째 항의 곱의 순서를 교환한 후 백캡 공식을 또한 적용합니다. 이때 외적의 곱의 순서를 바꾸면 음수가 붙게된다는 것을 상기하세요.
\tag{16}
\begin{align}
\vec B(\vec A \cdot \vec C) - \vec C (\vec A \cdot \vec B) +\vec C \times (\vec A \times \vec B)=0\\
\cancel{\vec B(\vec A \cdot \vec C)} - \vec C (\vec A \cdot \vec B) +\vec A(\vec B \cdot \vec C)-\cancel{\vec B(\vec C \cdot \vec A)} = 0
\end{align}결국 두개의 항이 남게 되요.
\tag{17}
\vec A (\vec B \cdot \vec C) - \vec C (\vec A \cdot \vec B) = 0만약 벡터 삼중곱의 결합 법칙이 성립한다면 (17)식이 반드시 성립해야 합니다. 즉 첫번째 항과 두번때 항의 크기가 항상 같아야 해요. 그러나 서로 다른 벡터 세 개가 곱해질 때 (17)식의 좌변이 항상 0이 된다는 보장은 전혀 없어요.
그래서 일반적으로 벡터 삼중곱은 비결합성을 갖게 됩니다.
4. 삼중곱의 잘못된 표현
지금까지 스칼라 삼중곱과 벡터 삼중곱에 대해 자세히 알아봤어요.
이번에는 삼중곱처럼 보이기는 하는데 얼밀히 말하면 삼중곱을 잘못 표기한 사례를 이야기 합니다.
예를 들면 다음의 식이 있어요.
\tag{18}
\vec A \times (\vec B \cdot \vec C)이 식도 표기상으로는 벡터 3개가 외적과 내적으로 서로 곱해지고 있어요. 얼핏 보면 삼중곱처럼 보입니다.
그러나 이 식은 잘 못되었어요. 왜냐면 (\vec B \cdot \vec C)를 계산하면 스칼라가 됩니다. 이 스칼라와 벡터 \vec A를 외적하고 있기 때문이에요.
외적은 벡터와 벡터끼리 곱하여 벡터가 되는 계산법이잖아요. 그런데 벡터와 스칼라를 외적하라고 했기 때문에 잘못 표현된 식이 됩니다.
(18)식은 다음과 같이 수정되어야 합니다.
\tag{19}
\vec A (\vec B \cdot \vec C)또 하나의 예입니다.
\tag{20}
\vec A \cdot (\vec B \cdot \vec C)(20)식은 어떤가요?
이 식도 잘 못 되었습니다. 왜냐면 (\vec B \cdot \vec C)를 계산하면 스칼라가 나오는데, 그 스칼라를 \vec A와 내적하라고 되어 있기 때문이에요.
내적도 벡터와 벡터 사이의 곱이 되어야만 합니다. 벡터와 스칼라 사이의 곱은 내적기호인 \cdot를 사용해서는 안됩니다.
즉 (20)식은 다음과 같이 수정되어야 합니다.
\tag{21}
\vec A (\vec B \cdot \vec C)지금까지 삼중곱에 대한 이야기였습니다.



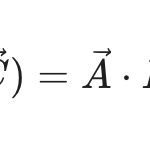
1 thought on “삼중곱”