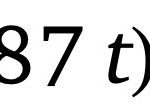VectorPlot: Mathematica

Last Updated on 2024-04-21 by BallPen

Mathematica로 화살표 벡터장 그리는 방법을 알아 봐요.

VectorPlot 명령어는 Mathematica에서 화살표로 벡터장을 그릴 때 사용됩니다.

이번 글에서는 그 VectorPlot 명령어의 사용법을 알아 볼게요. 이 명령어를 사용할 수 있으면 다양한 벡터장을 시각적으로 이해할 수 있게 됩니다.

아래는 이번 글의 목차입니다.

1. VectorPlot 기본 활용

예를 들어 아래의 2차원 벡터장(vector field)이 있다고 생각해봐요.

\tag{1}
\vec F = y \hat x -x \hat y

화살표를 이용해 이 벡터장을 표현하고 싶을 때 VectorPlot 명령어를 사용하면 됩니다. 아래의 코드를 Mathematica에 입력하고 실행해보세요.

이때 \{y,~-x \} 는 벡터장의 x성분과 y성분이고, \{ x,~ -3, ~3 \}은 x축의 범위를 -3에서 3까지 그리라는 의미입니다.

VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}]

그 결과 [그림 1]과 같이 벡터장을 그려줍니다. 이때 화살표의 색이 주황색으로 갈수록 벡터의 크기가 크고 파랑색으로 갈수록 벡터가 작아짐을 뜻해요.

또한 x축의 범위가 -3에서 3까지, y축의 범위도 -3에서 3까지 설정한대로 잘 그려졌습니다.

2. VectorPlot 옵션

VectorPlot에는 다양한 옵션들이 있어요. 몇가지만 소개합니다.

2-1. PlotLegend

아래와 같이 입력하면 화살표의 크기 정보를 알 수 있는 범례가 나옵니다.

VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}, PlotLegends -> Automatic]

2-2. ScalingFunctions

만일 x축의 눈금 스케일을 로그로 바꾸고 싶다면 다음과 같이 해보세요.

VectorPlot[{y, -x}, {x, 0, 3}, {y, -3,3}, PlotLegends -> Automatic, ScalingFunctions -> {"Log", None}]

2-3. PlotLayout

만일 한 그래픽에 두개의 Layout을 그리고 싶다면 다음과 같이 해보세요.

VectorPlot[{{y, -x}, {y, x + y}}, {x, -3, 3}, {y, -3, 3}, PlotLayout -> "Row"]

만일 [그림 4]처럼 Layout의 방향이 가로 방향이 아닌 세로방향으로 그리고 싶다면 코드에서 “Row” 대신에 “Column”을 입력하면 됩니다.

2-4. VectorSize

위에서 벡터의 크기가 색상으로 표현된다고 말씀드렸는데요. 만일 직접적으로 벡터의 크기를 화살표의 크기로 표현하고 싶다면 다음과 같이 해보세요.

VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}, VectorScaling -> Automatic, VectorSizes -> Automatic]

[그림 5]와 같이 벡터의 크기가 작으면 화살표가 작게 그려지고 벡터의 크기가 크면 화살표의 길이가 길게 표현된 것을 볼 수 있습니다.

만일 화살표의 크기를 Automatic이 아닌 직접 지정하고 싶다면 다음과 같이 해보세요.

VectorPlot[{y, -x}, {x, -3, 3}, {y, -3, 3}, VectorScaling -> Automatic, VectorSizes -> {0,1}]

3. 좌표계 변환을 통한 VectorPlot

만일 벡터장이 아래와 같이 극좌표계 형식으로 표현되었다면 벡터장을 어떻게 그려야 할까요?

\tag{2}
\vec E = {1 \over{r^2}}\hat r + (r + 2 \theta)\hat \theta

이때는 아래와 같이 극좌표계를 직각좌표계로 바꾼 후 VectorPlot하시면 됩니다.

VectorPlot[Evaluate[
    TransformedField["Polar" -> "Cartesian", {1/r^2, r+ 2\[Theta]}, {r, \[Theta]} -> {x, y}]
  ], {x, -3, 3}, {y, -3, 3}, VectorScaling->Automatic, VectorSizes->Automatic]

이번에는 아래 (3)식과 같이 r에만 의존하는 역제곱장을 생각해봐요. 마치 점전하에 의한 전기장과 같은 거죠.

\tag{3}
\vec E = {1 \over{r^2}}\hat r

이때에도 다음과 같이 입력하면 쉽게 그래픽을 만들어 낼 수 있어요.

VectorPlot[Evaluate[
    TransformedField["Polar" -> "Cartesian", {1/r^2, 0}, {r, \[Theta]} -> {x, y}]
  ], {x, -3, 3}, {y, -3, 3}, VectorScaling->Automatic, VectorSizes->Automatic]

Related posts.

1계 선형 미분방정식 풀이 방법 cot(wt) 적분 (csc(wt))^2 적분 이차방정식 풀이 벡터 화살표 그리기 | WolframAlpha 제차 이계 상미분 방정식 : 상수 계수 함수의 그래프 그리기 | WolframAlpha 상미분방정식 풀이 | WolframAlpha