Last Updated on 2023-01-23 by BallPen
직각좌표계 정의와 직각좌표계에서 위치, 속도, 가속도 등을 어떻게 표현하는지 알아 보겠습니다.
직각좌표계(cartesian coordinate system)란 직교좌표계의 한 종류입니다.
직각좌표계를 이용하여 공간상에 있는 어떤 입자의 위치, 속도, 가속도 등을 어떻게 표현하는지 함께 알아보겠습니다.
아래는 이번 글의 목차입니다.
Contents
1. 직각좌표계 정의
공간상에 어떠한 입자(또는 물체)가 있을 때 그 입자가 있는 위치를 정확하게 표현하는 방법이 필요합니다.
이를 위해 물체가 단위벡터 \hat {x}방향으로 x m, \hat {y}방향으로 y m 떨어진 곳에 있다는 방식을 일반적으로 사용하는데요.
이때 사용하는 좌표계를 직각좌표계라고 합니다. 직각좌표계를 사용하면 공간상의 어느 지점이든 좌표를 만들어 낼 수 있어요.
아래 [그림 1]은 자동차 공장에 있는 용접로봇을 보여주고 있습니다.
![[그림 1] 독일 Leipzig에 있는 BMW 공장의 용접 로봇.](https://ballpen.blog/wp-content/uploads/2023/01/BMW_Leipzig_MEDIA_050719_Download_Karosseriebau_max-1024x683.jpg)
이 로봇들은 자동차가 컨베이터벨트에 실려 계속 이동하는 동안 차체의 여러곳을 용접하는데요. 용접할 부위의 공간 좌표를 지정해 놓으면 로봇은 그 위치로 용접봉을 이동하여 용접하게 됩니다.
그렇다면 직각좌표계를 활용해 2차원과 3차원에서의 좌표 만드는 법을 알아봐요.
1-1. 2차원 직각좌표계
2차원이란 x축과 y축으로 구성된 평면 공간을 말합니다.
여기서 평면공간이란 아래 [그림 2]와 같이 대표적으로 당구대를 생각해 볼 수 있어요.
![[그림 2] 당구장의 당구대는 대표적인 2차원 직각좌표계 평면공간으로 간주할 수 있습니다. (그림 인용 : pxhere.com)](https://ballpen.blog/wp-content/uploads/2023/01/당구장.jpeg)
당구대는 평면이며 그 위에 당구공이 위치해 있습니다. 이때 당구공의 위치를 표현하기 위해서는 x축과 y축만 있으면 돼요.
아래 [그림 2]는 2차원 직각좌표계에서 위치 좌표에 대한 예시입니다.
![[그림 3] 2차원 직각좌표계 좌표 표현 (그림 인용: 위키백과)](https://ballpen.blog/wp-content/uploads/2023/01/Cartesian-coordinate-system-1024x1024.jpg)
그림과 같이 2차원 직각좌표계에서 좌표는 (x,y)로 나타냅니다. 수학시간에 공부하던 좌표 표현법과 같아요.
예를 들어 단위벡터 \hat {x}축 방향으로 2 m, \hat{y}축 방향으로 3 m 떨어진 곳에 어떤 물체가 있다면 그 물체의 좌표는 (2,3)m로 표현하는 방식이죠.
그렇다면 3차원 직각좌표계는 어떻게 좌표를 표현할까요?
1-2. 3차원 직각좌표계
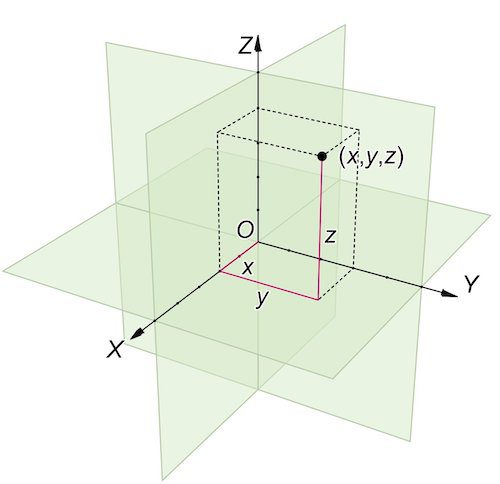
아래 [그림 4]는 3차원 직각좌표계에서 어느 입자의 위치를 나타냅니다.
![[그림 4] 3차원 직각좌표계 좌표 표현 (그림 인용 : 위키백과)](https://ballpen.blog/wp-content/uploads/2023/01/Coord_system_CA_0-1024x991.jpg)
만일 어떤 물체가 \hat{x}방향으로 x m, \hat{y}방향으로 y m, \hat{z}방향으로 z m 떨어진 곳에 있다면 그 위치는 (x,y,z)로 표현합니다.
2차원 좌표에서 z축 방향의 성분이 하나 더 추가된 것이 3차원 직각좌표계에서의 좌표 표현법입니다.
2. 직각좌표계에서의 위치, 속도, 가속도
이번에는 직각좌표계에서 어떤 입자의 위치, 속도, 가속도 표현법을 알아보겠습니다. 왜 이것까지 알아야 하지?라고 생각할 수 있지만, 그 이유는 공간상의 물체가 멈춰있기도 하지만 움직이기도 하기 때문이에요.
따라서 직각좌표계에서 어떤 입자의 위치, 속도, 가속도를 정의하는 것은 아주 중요합니다.
우선 위치부터 알아보겠습니다.
2-1. 위치
직각좌표계에서 어떤 물체의 위치를 표현하는 가장 쉬운 방법은 위에서 설명드린 좌표 (x,y,z)를 활용하는 것입니다.
그러면 어느 시간에 물체의 위치에 대한 정보가 완벽히 표현되는 거에요.
하지만 과학이나 공학에서는 어떤 입자의 위치를 나타낼 때 위치벡터를 사용하는 것이 더욱 일반적입니다.
그 이유는 위치, 속도, 가속도를 모두 벡터로 표현하고 싶기 때문이에요. 좌표 (x,y,z)와 위치벡터는 다음의 관계를 갖습니다.
\tag{1}
\begin{align}
(x,y,z) =\vec{r} = x \hat x + y \hat y + z \hat
z
\end{align}(1)식에서 x,~y,~z는 직각좌표계에서 각 방향의 좌표 크기를 나타내고, \hat x, \hat y, \hat z는 각 방향의 단위벡터를 의미합니다.
한편 기준점으로부터 입자가 있는 곳까지의 거리 |\vec r|는 피타고라스 정리에 의해 다음과 같이 주어지게 되겠죠.
\tag{2}
\begin{align}
|\vec r| = \sqrt{x^2 + y^2 + z^2}
\end{align}예를 들어 아래 [그림 5]는 3차원 직각좌표계 공간에서 좌표 (3, 4, 10)에 어떤 입자가 있을 때 그 입자의 위치벡터를 빨강색 화살표로 표현한 것입니다.
![[그림 5] 직각좌표계 공간에서의 위치 벡터](https://ballpen.blog/wp-content/uploads/2023/01/Picture1-2-793x1024.jpg)
이때 위치벡터 \vec r, 기준점으로부터 입자가 있는 곳까지의 거리 |\vec r|는 다음과 같이 표현됩니다.
\tag{3}
\begin{align}
\vec{r} &= 3 \hat x + 4\hat y + 10 \hat z\\
\end{align}\tag{4}
\begin{align}
|\vec r| &= \sqrt{3^2 + 4^2 + 10^2}\\
& \approx11.2
\end{align}2-2. 변위와 속도
직각좌표계에서 입자의 위치가 시간에 따라 달라진다면 그 입자는 움직이고 있음을 뜻합니다.
이와 같이 어느 시간 dt동안 입자가 움직인 변위 d \vec r의 비율을 속도 \vec v라고 합니다.
이때 최초 (x,y,z)에서 나중 (x^{\prime}, y^{\prime}, z^{\prime})로 입자의 위치가 변했다면 변위 벡터 d \vec r은 아래 [그림 6]과 같이 표현됩니다.
![[그림 6] 직각좌표계 공간에서의 변위 벡터](https://ballpen.blog/wp-content/uploads/2023/01/Picture1-5-966x1024.jpg)
이를 식으로 표현하면 다음과 같아요. 두 위치 벡터사이의 뺄셈이 변위 벡터가 됩니다.
\tag{5}
\begin{align}
d \vec r &= \vec {r^{\prime}} - \vec r\\
&= ({x^{\prime}} \hat x + {y^{\prime}}\hat y + {z^{\prime}}\hat z) - ( {x} \hat x + {y}\hat y + {z}\hat z)\\
&=(x^{\prime} - x)\hat x + (y{^\prime} - y)\hat y + (z^{\prime} - z)\hat z\\
&=dx \hat x + dy \hat y + dz \hat z
\end{align}또한 변위벡터 d \vec r의 크기, 즉 처음 위치와 나중 위치 사이의 거리 |d \vec r|은 다음과 같습니다.
\tag{6}
|d \vec r| = \sqrt{dx^2 + dy^2 + dz^2}따라서 속도는 다음과 같이 정의됩니다.
\tag{7}
\begin{align}
\vec v = {{d\vec r}\over{dt}} &={{dx \hat x + dy \hat y + dz \hat z}\over{dt}}\\
&={dx \over dt} \hat x + {dy \over dt}\hat y + {dz \over dt}\hat z\\
&=v_x \hat x + v_y \hat y + v_z \hat z
\end{align}한편 속도의 크기인 속력은 다음과 같아요.
\tag{8}
|\vec v| = \sqrt{v_x^2 + v_y^2 + v_z^2}2-3. 가속도
속도가 정의되었으니 가속도 \vec a를 다음과 같이 정의할 수 있습니다.
\tag{9}
\begin{align}
\vec a = {dv \over dt}&={{v_x \hat x + v_y \hat y + v_z \hat z}\over{dt}}\\
&={v_x \over dt} \hat x + {v_y \over dt}\hat y +{v_z \over dt} \hat z\\
&=a_x \hat x + a_y \hat y + a_z \hat z
\end{align}또한 가속도의 크기는 다음과 같습니다.
\tag{10}
|\vec a| = \sqrt{a_x ^2 + a_y ^2 + a_z ^2}3. 미소면적요소와 미소체적요소
아래 [그림 7]은 직각좌표계에서의 미소면적요소와 미소체적요소(또는 미소부피요소)를 구하기 위한 그림입니다.
![[그림 7] 직각좌표계 미소면적요소와 미소부피요소](https://ballpen.blog/wp-content/uploads/2023/01/Picture1-6-744x1024.jpg)
3-1. 미소면적요소
직각좌표계의 미소면적요소는 벡터량입니다.
미소면적요소의 크기는 가로와 세로의 미소길이 사이의 곱으로 구하고, 방향은 그 평편에 수직한 방향으로 정의합니다.
따라서 [그림 7]에 표기된 세 개의 미소면적요소는 다음 (11)식과 같이 정의됩니다. 만일 크기만을 고려하고자 한다면 아래의 식에서 단위벡터만 무시하면 됩니다.
\tag{11}
\begin{align}
d \vec A_x = (dy ~dz) \hat x\\
d \vec A_y = (dx ~dz) \hat y\\
d \vec A_z = (dx ~dy) \hat z\\
\end{align}위 세개의 미소면적요소에 반대되는 면에 대한 미소면적요소는 다음과 같아요. 크기는 같으나 방향이 반대이므로 음의 부호가 붙습니다.
\tag{12}
\begin{align}
d \vec A_{-x} = (dy ~ dz) (-\hat x)=-(dy ~ dz) (\hat x)\\
d \vec A_{-y} = (dx ~ dz) (-\hat y)=-(dx ~ dz) (\hat y)\\
d \vec A_{-z} = (dx ~ dy) (-\hat z)=-(dx ~ dy) (\hat z)\\
\end{align}3-2. 미소체적요소
이번에는 미소체적요소입니다. 미소체적요소는 스칼라량입니다.
체적이 가로, 세로, 높이의 곱으로 정의되므로 [그림 7]에 있는 미소부피는 다음과 같이 정의됩니다.
\tag{13}
dV = (dx ~ dy ~ dz)



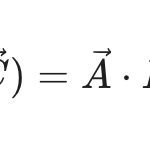
6 thoughts on “직각좌표계 (cartesian coordinate system)”