Last Updated on 2025-10-24 by BallPen
이상기체의 요건과 이상기체 상태방정식을 알아 봐요.
이상기체(ideal gas)란 이상기체 상태방정식을 만족하는 기체를 말해요.
물론 실제 기체가 이상 기체처럼 행동할 수는 없어요. 그럼에도 온도가 높거나 낮은 압력에서는 이상 기체처럼 다룰 수 있답니다.
이번 글에서는 이상기체의 요건과 이상기체가 만족하는 이상기체 상태방정식을 알아 봐요.
1. 이상기체의 요건
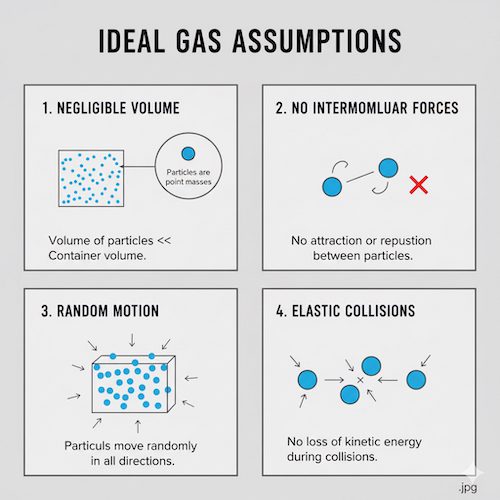
이상기체는 탄성충돌 이외의 다른 상호작용을 하지 않는 점입자로 구성된 기체 모형이에요. 이상기체의 요건은 다음과 같아요.
(1) 기체는 무수히 많은 동일한 분자들로 구성되어 있다. 분자의 수가 많다는 사실은 분자의 성질을 통계적으로 해석해야 함을 의미한다.
(2) 분자 크기에 비해 분자 간 거리는 멀리 떨어져 있다. 이는 반대로 분자 자체의 부피를 0으로 간주함을 의미하며, 또한 분자들 사이의 상호작용을 무시한다는 의미이다.
(3) 분자들의 운동은 무질서하게 움직인다. 이 말은 분자들이 움직일 때 어느 방향이든지 같은 확률로 움직인다는 것을 뜻한다.
(4) 분자들은 딱딱한 구로 취급한다. 분자간의 충돌은 탄성충돌이고 운동량과 운동에너지가 보존된다.
(5) 분자들은 뉴턴의 운동 법칙을 따른다.
실제 기체는 이상기체와는 분명히 달라요. 하지만 기체의 온도가 높거나 낮은 압력에서는 실제 기체를 이상기체로 볼 수 있어요.
왜냐면 온도가 높으면 기체분자들의 운동에너지가 커 빠르게 움직이고 압력이 낮으면 분자들 간의 거리가 멀리 떨어져 서로 간의 상호작용을 무시할 수 있기 때문이에요. 즉 위 요건에서 다른 모든 요건 뿐만 아니라 (2)번째 요건을 더욱 충실하게 만족하기 때문이죠.
2. 이상기체 법칙
2-1. Boyle, Charles, Gay-Lussac의 법칙
이상 기체의 법칙은 보일(Boyle), 샤를(Charles), 게이-뤼삭(Gay-Lussac)의 법칙을 일반화 한 것인데요. 이 법칙들에 대해 잠시만 알아 봐요.
보일의 법칙은 기체의 양과 온도가 일정할 때 압력 P와 부피 V는 서로 반비례한다는 법칙입니다.
\tag{2-1}
\begin{align}
P \propto {1 \over V}
\end{align}샤를의 법칙은 기체의 양과 압력이 일정할 때 부피 V는 온도 T에 비례한다는 법칙입니다.
\tag{2-2}
\begin{align}
V \propto T
\end{align}마지막으로 게이-뤼삭의 법칙은 기체의 양과 부피가 일정할 때 압력 P는 온도 T에 비례한다는 법칙입니다.
\tag{2-3}
\begin{align}
P \propto T
\end{align}2-2. 이상기체 법칙(이상기체의 상태방정식)
보일의 법칙, 샤를의 법칙, 게이-뤼삭의 법칙을 종합적으로 일반화하면 다음과 같이 쓸 수 있어요.
\tag{2-4}
\begin{align}
PV = nRT
\end{align}이 식을 거시적으로 기술한 이상기체 법칙(ideal gas law) 또는 이상기체의 상태방정식(equation of state for an ideal gas)이라고 해요.
식에서 n은 기체의 몰수로서 기체의 양을 나타내는 척도입니다. 즉, 다음과 같이 아보가드로수 N_A 대비 기체분자수 N이 얼마나 있느냐의 척도로 정의합니다.
\tag{2-5}
n = {N \over N_A}아보가드로수는 N_A = 6.022 \times 10^{23}~개/{\rm mol}입니다.
또한 식에서 R은 비례상수로서 모든 기체에 대해 같은 값을 갖습니다. 이 상수는 보편기체상수(universal gas constant)라 하며 그 값은 아래와 같습니다.
\tag{2-6}
\begin{align}
R = 8.315~\rm {J/(mol~ K)}
\end{align}한편 (2-5)식을 (2-4)식에 대입한 후 상수끼리 묶고 정리하면 다른 형태의 이상기체 방정식을 얻을 수 있어요.
\tag{2-7}
\begin{aligned}
PV &= nRT\\[10pt]
&= {N \over N_A} RT\\[10pt]
&=N \Big({R \over N_A} \Big) T
\end{aligned}이때 윗 식에서 괄호는 또 하나의 상수가 될 뿐이에요. 그래서 이를 k_B로 치환하면 다음과 같아요.
\tag{2-8}
\begin{align}
PV = Nk_BT
\end{align}이때 k_B는 볼츠만상수(Boltzmann’s constant)라 하며 k_B=1.38 \times 10^{-23}~\rm{J/K}의 크기를 갖습니다.


“이상기체 (ideal gas)”에 대한 2개의 생각