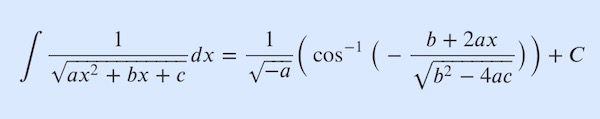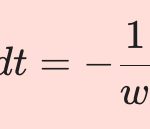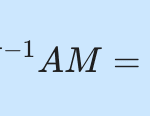Last Updated on 2025-09-06 by BallPen
재미있는 적분 문제 하나를 풀어 보도록 해요.
과학을 하다보면 여러 적분 문제를 풀게 되는데요.
그중에서 아래 문제가 어떻게 풀어지게 되는지 구해보도록 해요. 이때 \(a<0\)으로 가정하겠습니다.
\begin{align}
\int{{1}\over{\sqrt{ax^2 + bx +c}}}dx = {1 \over{\sqrt{-a}}} \Big(\cos^{-1}\big(-{{b+2ax}\over{\sqrt{b^2 -4ac}}}\big)\Big) + C
\end{align}
그리고 윗 식에서 대문자 \(C\)는 적분상수입니다.
[풀이] \(P\)로 주어진 다음 적분을 풀어 봐요.
\begin{align}
\tag{1}
P=\int{{1}\over{\sqrt{ax^2 + bx +c}}}dx
\end{align}
먼저 위 적분에서 근호안에 있는 \(ax^2 + bx + c\)를 다음과 같이 변형합니다.
\begin{align}
\tag{2}
ax^2 + bx +c &= a \big( x^2 + {{b}\over{a}}x + {{c}\over{a}}\big)\\[8pt]
&=a\Big(\big( x + {{b}\over{2a}}\big)^2 – {{b^2}\over{4a^2}} + {{c}\over{a}}\Big)\\[8pt]
&=a \Big( \big( x + {{b}\over{2a}}\big)^2 + {{4ac – b^2}\over{4a^2}}\Big)
\end{align}
그리고 위 (2)식을 (1)식에 대입하고 정리합니다.
\begin{align}
\tag{3}
P &=\int{1 \over{\sqrt{a \Big( \big( x + {{b}\over{2a}}\big)^2 + {{4ac – b^2}\over{4a^2}}\Big)}}}dx\\[8pt]
&={1 \over{\sqrt{-a}}} \int {1 \over{\sqrt{{b^2 -4ac}\over{4a^2}}-\big(\color{blue}{x+ {{b}\over{2a}}}\big)^2}}dx
\end{align}
윗 식에서 상수 \(1 \over{\sqrt{-a}}\)를 적분 기호 밖으로 꺼냈는데요. 굳이 근호 안을 \(-a\)로 꺼낸 이유는 \(a<0\)인 조건을 가정했기 때문에 \(1 \over{\sqrt{-a}}\)로 꺼내더라도 실수가 됨을 아실 수 있을 거에요.
또한 위 식의 파랑색 수식을 \(t\)로 치환해봐요. 그러면 다음과 같은 관계가 성립합니다.
\begin{align}
\tag{4}
&t=x+{b \over {2a}},~~~{{dt}\over{dx}}=1,~~~dx=dt
\end{align}
(3)식에 (4)식의 치환 관계를 반영합니다.
\begin{align}
\tag{5}
P={1 \over{\sqrt{-a}}} \int {1 \over{\sqrt{\Big( {\color{red} {{\sqrt{{b^2 – 4ac}}}\over{2a}}} \Big)^2 – t^2}}}dt
\end{align}
치환을 한번 더 합니다. 윗 식에서 빨강색 부분은 상수일 뿐이므로 아래와 같이 \(u\)로 치환해봐요.
\begin{align}
\tag{6}
u = {{\sqrt{b^2 – 4ac}}\over{2a}}
\end{align}
그러면 (5)식은 다음과 같이 간결하게 쓸 수 있어요.
\begin{align}
\tag{7}
P={1 \over{\sqrt{-a}}} \int{1 \over{\sqrt{u^2 – t^2}}} dt
\end{align}
여기서 한번 더 치환을 할 건데요. 윗 식에서 \(t\)를 다음과 같이 치환하도록 해봐요.
\begin{align}
\tag{8}
t = -u \cos k,~~~{{dt}\over{dk}} = u \sin k,~~~dt = u \sin k dk
\end{align}
위 치환 관계를 (7)식에 대입하면 아래와 같습니다.
\begin{align}
\require{cancel}
\tag{9}
P&={1 \over{\sqrt{-a}}} \int {{u \sin k}\over{\sqrt{u^2 – u^2 \cos^2 k}}}dk\\[8pt]
&={1 \over{\sqrt{-a}}}\int {{u\sin k}\over{\sqrt{u^2 (1-\cos^2 k)}}}dk\\[8pt]
&={{1}\over{\sqrt{-a}}} \int {{{\cancel {u \sin k}}}\over{\cancel{u\sin k}}}dk\\[8pt]
&={{1}\over{\sqrt{-a}}}\int 1 dk\\[8pt]
&={{1}\over{\sqrt{-a}}} (k + C)
\end{align}
대문자 \(C\)는 적분상수를 뜻합니다. 이제 윗 식의 마지막 줄의 \(k\)에 (8)식, (6)식, (4)식에서 치환했던 식을 모두 원래로 되돌립니다.
\begin{align}
\tag{10}
P &= {1 \over{\sqrt{-a}}}\Big( \cos^{-1} \Big({-{{t}\over{u}}}\Big)+C\Big)\\[8pt]
&={1\over{\sqrt{-a}}} \Big( \cos^{-1}\Big(-{{x+{b\over {2a}}}\over{{\sqrt{b^2 – 4ac}}\over{2a}}}\Big) + C \Big)\\[8pt]
&={1\over{\sqrt{-a}}} \Big( \cos^{-1} \Big( -{{{b+2ax}\over{\cancel{2a}}}\over{{\sqrt{b^2 – 4ac}}\over{\cancel{2a}}}}\Big) + C \Big)\\[8pt]
\end{align}
결국 윗 식을 정리하면 다음과 같습니다. 이때 \({C/{\sqrt{-a}}}\)는 또 다른 상수가 될 뿐이므로 간단히 \(C\)로 표기했어요.
\begin{align}
\tag{11}
\int{{1}\over{\sqrt{ax^2 + bx +c}}}dx={1\over{\sqrt{-a}}} \Big( \cos^{-1} \big(-{{b+2ax}\over{\sqrt{b^2 -4ac}}}\big)\Big)+C
\end{align}