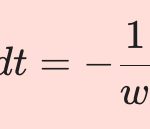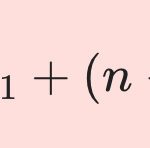테일러 급수 증명과 활용 사례

BallPen · 2022-03-30T23:16:46+09:00

테일러 급수 전개 또는 테일러 급수란 어떤 함수를 특정 점의 미분계수들을 계수로 하는 다항식으로 표현한 것을 말합니다. 이 급수는 과학 분야에서 근사식을 마련하는데 많이 활용됩니다. 이번 글에서는 테일러 급수의 정의, 활용사례, 증명을 다룹니다.

Last Updated on 2024-01-06 by BallPen

테일러 급수는 자연과학이나 공학 분야에서 많이 사용되는데요. 이에 대한 증명과 활용 사례를 다룹니다.

테일러 급수 전개(Taylor series expansion) 또는 테일러 급수(Taylor series)는 이항정리와 함께 과학분야에서 자주 활용됩니다.

이번 글에서는 테일러 급수 정의, 활용 사례, 증명에 대한 내용이 주로 다루어 집니다. 테일러 급수가 궁금한 사람에게 큰 도움이 될 거에요.

아래는 이번 글의 목차입니다.

Contents

1. 테일러 급수
2. 테일러 급수 활용 사례
3. 테일러 급수 증명

1. 테일러 급수

테일러 급수란 어떤 함수를 특정 점의 미분계수들을 계수로 하는 다항식으로 표현한 것을 말합니다. 이 급수의 정의와 의미를 알아보겠습니다.

1-1. 테일러 급수 정의

테일러 급수의 모양은 아래 (1)식과 같습니다.

\tag{1} \begin{align} \color{black} f(x)=f(a)+ (x-a)f^{\prime}(a) + {{(x-a)^2}\over{2 !}}f^{\prime\prime}(a)+{{(x-a)^3}\over{3!}}f^{\prime\prime\prime}(a)+\cdots \color{red} \end{align}

(1)식의 테일러 급수 증명은 본 글의 가장 마지막에 제시하였습니다. 노트를 펴고 한번쯤은 따라서 유도해보면 좋을 것 같아요.

(1)식에 있는 ! 기호는 팩토리얼(factorial)이라고 합니다. 2!은 $2\times1$ , 3!은 $3 \times 2 \times1$ 을 의미합니다.

(1)식은 보통 $a$ 점 근처에서 성립하는 테일러 급수라고 합니다.

한편 $a=0$ 인 경우 식은 아래와 같이 변경됩니다. 그리고는 이것을 맥클로린 급수(Maclaurin series)라고도 부릅니다.

\tag{2} \begin{align} \color{black} f(x)=f(0)+ xf^{\prime}(0) + {{x^2}\over{2 !}}f^{\prime\prime}(0)+{{x^3}\over{3!}}f^{\prime\prime\prime}(0)+\cdots \color{red} \end{align}

맥클로린 급수는 0점 근처에서 성립하는 테일러 급수로 이해하시면 됩니다.

1-2. 테일러 급수 의미

테일러 급수는 $a$ 점 또는 0점 근처에서 어느 함수를 근사하기 위해 사용되는 경우가 많은데요. 차근차근 예를 들어 설명드리겠습니다.

어떤 함수 $f(x)$ 가 $e^x$ 로 주어졌다고 생각해 보세요. 이 지수함수는 한번 미분해도 $e^x$ , 두번 미분해도 $e^x$ 가 되므로 간단한 예시에 활용하기 좋아요.

\tag{3} f(x) = e^{x}

[용어정의]

$f(x)$ 는 어떤 변수 $x$ 를 함수에 대입하여 계산한 값인 함수 값을 의미합니다. 같은 방식으로 $f(a)$ 는 임의의 값 $a$ 를 함수에 대입하였을때의 함수값을 말해요.

그리고 $f^{\prime}(a)$ 란 함수를 한번 미분한 식에 $a$ 를 대입하라는 의미입니다. 이것을 전문용어로 $a$ 지점에서 도함수의 미분계수라고 합니다.

같은 방식으로 $f^{\prime\prime}(a)$ 란 함수를 두번 미분한 식에 $a$ 를 대입하라는 의미가 되고, 이것은 $a$ 지점에서 이계도함수의 미분계수라고 부릅니다.

[계속]

(3)식의 함수 $f(x)=e^{x}$ 를 (1)식의 테일러급수 좌변에 대입하면 아래와 같습니다.

\tag{4} \begin{align} \color{black} f(x) = e^{x}=f(a)+ (x-a)f^{\prime}(a) + {{(x-a)^2}\over{2 !}}f^{\prime\prime}(a)+{{(x-a)^3}\over{3!}}f^{\prime\prime\prime}(a)+\cdots \color{red} \end{align}

그리고 (4)식의 우변에 $a$ 대신에 5.00의 값을 대입해봐요.

\tag{5} \begin{align} \color{black} f(x)=e^x &=f(5.00)+ (x-5.00)f^{\prime}(5.00) + {{(x-5.00)^2}\over{2 !}}f^{\prime\prime}(5.00)\\ &~~~~~~~~~+{{(x-5.00)^3}\over{3!}}f^{\prime\prime\prime}(5.00)+\cdots \end{align}

그리고 이번에는 (5)식에 있는 모든 $x$ 대신에 $a=5.00$ 근처의 값인 5.01을 대입해 보세요.

그러면 (5)식의 좌측에 있는 $f(x)=e^{x}$ 의 계산 결과는 아래와 같습니다.

\tag{6} \begin{align} f(5.01) = e^{5.01} &= 149.904~736~1\\ \end{align}

한편 (5)식의 우변은 항이 많아서 복잡하기는 한데요. 첫번째 항만 계산했을 때, 두번째 항까지 계산했을 때, 세번째 항까지 계산했을 때를 각각 보면 아래와 같습니다.

\tag{7} \begin{align} f(5.00) =e^{5.00} &= 148.413~159~1\\[10pt] f(5.00)+(5.01-5.00)f^{\prime}(5.00) =e^{5.00}+(0.01)e^{5.00} &= 149.897~290~7\\[10pt] (149.897~290~7) +{{(5.01-5.00)^2}\over{2}}f^{\prime\prime}(5.00)&=149.904~711~4 \end{align}

위 식에서 첫번째 줄은 (5)식의 우변 첫번째 항만으로 구한 값인데요. (6)식의 좌변 계산결과와 완전히 같지는 않으나 거의 비슷한 크기가 얻어졌어요. 그러나 오차는 우변의 항이 추가될 수록 점점 감소합니다. (7)식의 두번째 줄은 (5)식의 우변 두번째 항까지의 계산 결과이며, 세번째 줄은 세번째 항까지의 계산 결과에요.

보는바와 같이 우변의 항이 추가될수록 좌변의 계산 값에 점점 가까워 지는 것을 알 수 있어요.

결국 (1)식에 주어진 테일러 급수가 성립한다는 것을 알 수 있습니다.

그런데 여기서 중요한 것은 (1)식의 테일러급수를 최대한 활용하기 위해서는 $a$ 값과 $x$ 값이 비슷할수록 좋아요. 즉 $(x-a)$ 값이 1보다 작게되면 $(x-a)^2$ 은 1보다 더욱 작아지고 $(x-a)^3$ 은 1보다 아주 작아져 무시 가능할 만큼 작은 크기가 될거에요.

결국 (1)식은 $(x-a)$ 값이 1보다 작은 경우 다음과 같이 앞에 있는 몇 개의 항을 활용하여 테일러 급수 선형근사 식을 만들어 낼 수 있답니다. 물론 항을 더욱 추가할수록 오차는 줄어들어요.

\tag{8} \begin{align} \color{black} f(x) \approx f(a)+ (x-a)f^{\prime}(a) \end{align}

다시 한번 더 말씀드리면 (8)식의 근사식을 활용하기 위해서는 $x$ 가 $a$ 값 근처로 주어져야 합니다.

만일 $x$ 가 $a$ 와 멀리 떨어진 값이라면 (8)식과 같이 간단하게 근사할 수 없고 더 많은 항을 추가해야 합니다.

그렇다면 $a=0$ 을 대입한 (2)식은 무슨 의미를 가질까요. 그것은 바로 $x$ 가 0점 근처의 값을 가질때 활용할 수 있는 테일러 급수 입니다.

$x$ 값이 0점과 아주 비슷하여 1보다 작은 값을 가질 경우 $x^2$ 은 더욱 작아지고, $x^3$ 은 아주 더욱 작아져 무시가능한 크기를 갖게 될거에요.

그러면 아래와 같이 (2)식의 앞에 있는 몇 개의 항을 활용하여 테일러 급수 선형근사 식을 만들어 낼 수 있게 됩니다.

\tag{9} \begin{align} \color{black} f(x)\approx f(0)+ xf^{\prime}(0) \end{align}

1.3. 몇가지 함수에 대한 테일러 급수

0점 근처에서의 테일러 급수 전개식을 다시 쓰면 아래와 같습니다.

\tag{10} \begin{align} \color{black} f(x)=f(0)+ xf^{\prime}(0) + {{x^2}\over{2 !}}f^{\prime\prime}(0)+{{x^3}\over{3!}}f^{\prime\prime\prime}(0)+\cdots \color{red} \end{align}

예를 들어 $e^x$ 의 함수가 있을 때 원점 근처에서의 테일러 급수를 네번째 항까지 구하면 아래와 같습니다.

\tag{11} \begin{align} f(0) = e^{0} &= 1\\ xf^{\prime}(0) =x\cdot e^{0} &= x\\ {{x^2}\over{2!}}f^{\prime\prime}(0) = {{x^2}\over{2\times1}}\cdot e^{0} &={{x^2}\over{2}} \\ {{x^3}\over{3!}}f^{\prime\prime\prime}(0) = {{x^3}\over{3\times 2 \times 1}}\cdot e^{0} &={{x^3}\over{6}} \\ \end{align}

결국 다음이 성립하는 거에요.

\tag{12} \begin{align} e^x = 1+x + {{x^2}\over{2}} + {{x^3}\over{6}} + \cdots \end{align}

그렇다면 정말 원점 근처에서 (12)식이 성립하는지 그래프를 그려 확인해 보겠습니다.

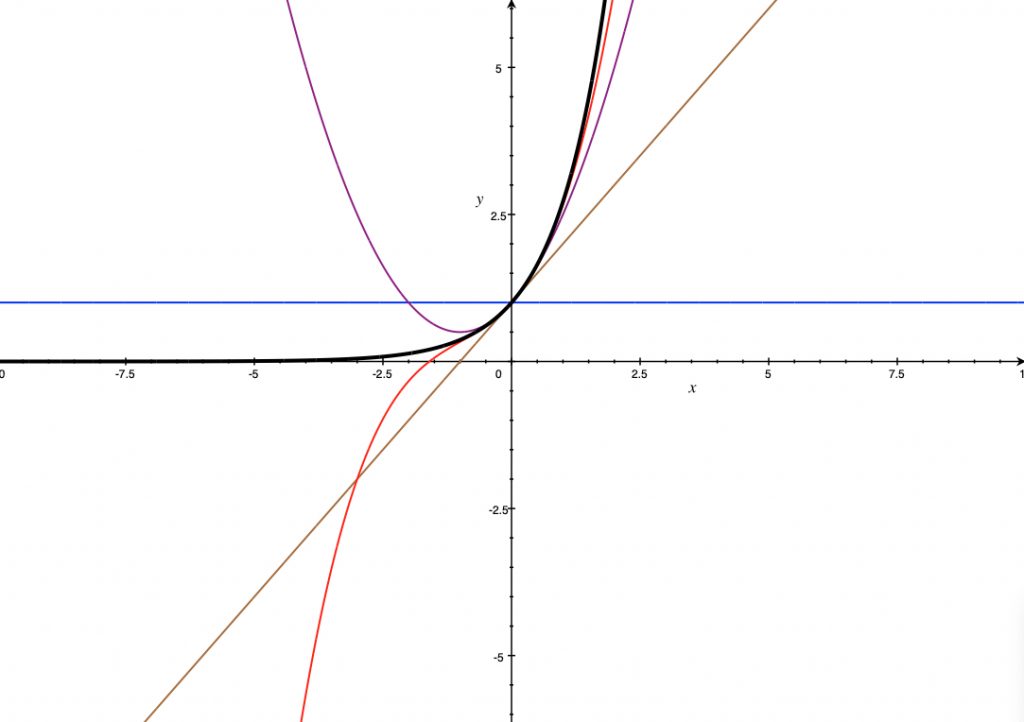
[그림 1] 테일러 급수 전개식의 항이 추가될수록 원점근처에서 원래 함수의 곡선 모양과 점점 일치해가는 것을 알 수 있습니다. 검정색이 원래 함수의 곡선이고 파랑색은 첫번째항, 갈색은 두번째 항까지, 보라색은 세번째 항까지, 빨강색은 네번째 항까지의 곡선을 나타냅니다.

[그림 1]에서 진한 검정색 선은 원래함수인 $e^x$ 이고, 파랑색 선은 $1$ , 갈색 선은 $1+x$ , 보라색 선은 $1+x+{x^2 / 2}$ , 빨강색 선은 $1+x+{x^2 / 2} + {x^3 / 6}$ 을 나타냅니다.

그림과 같이 항이 늘어날 수록 원점 근처에서 원래 함수의 곡선 모양과 일치하는 범위가 점점 넓어지는 것을 알 수 있습니다.

이번에는 $\sin x$ 의 원점근처에서의 테일러 급수를 구해보죠. 방법은 위에서 했던 방식 그대로 적용하면 됩니다.

\tag{13} \begin{align} f(0) = \sin{0} &= 0\\ xf^{\prime}(0) =x\cdot \cos{0} &= x\\ {{x^2}\over{2!}}f^{\prime\prime}(0) = -{{x^2}\over{2!}}\cdot \sin{0} &=0 \\ {{x^3}\over{3!}}f^{\prime\prime\prime}(0) = -{{x^3}\over{3!}}\cdot \cos{0} &=-{{x^3}\over{3!}} \\ {{x^4}\over{4!}}f^{\prime\prime\prime\prime}(0) = {{x^4}\over{4!}}\cdot \sin{0} &=0 \\ {{x^5}\over{5!}}f^{\prime\prime\prime\prime\prime}(0) = {{x^5}\over{5!}}\cdot \cos{0} &={{x^5}\over{5!}} \\ \end{align}

결국 다음이 성립하는 거에요.

\tag{14} \sin x = x - {{x^3}\over{3!}} + {{x^5}\over{5!}} + \cdots

기타 다양한 함수의 급수는 위키백과를 참고하세요.

2. 테일러 급수 활용 사례

두개의 원자로 구성된 분자가 있을 때 두 원자 사이의 위치에너지는 다음의 Morse 위치에너지 함수로 주어집니다.

\tag{15} V(x) = V_0 \Big[1-e^{-(x-x_0)/\delta }\Big ] ^2 - V_0

여기서 $V_0$ , $\delta$ 는 상수입니다. 또한 $x_0$ 는 두 원자 사이의 평형거리이고, $x$ 는 어느 순간 두 원자사이의 떨어진 거리입니다. 그런데 이때 두 원자사이의 떨어진 거리가 평형거리보다 아주 약간 차이가 있는 정도라고 가정하겠습니다.

그러니까 원자 끼리의 거리 $x$ 가 평형거리 $x_0$ 근처에서 아주 미세하게 진동하는 것을 상상하세요.

어느 정도냐면 $x-x_0$ 의 크기가 1보다 아주 작은 정도로요. 결국 이렇게 가정함으로써 $x_0$ 근처에서의 테일러 급수를 적용할 수 있게 됩니다.

그러면 (15)식에서 대괄호안에 있는 지수항은 (12)식의 테일러급수를 적용하여 간단하게 근사할 수 있어요. 이때 (12)식의 $x$ 를 $-(x-x_0 ) /\delta$ 로 보시면 됩니다.

\tag{16} \begin{align} V(x) &= V_0 \Big[1-e^{-(x-x_0)/\delta }\Big ] ^2 - V_0\\ &=V_0\Big[1-\big[ \color{red}1+{{\big(-(x-x_0)/\delta \big) + \color{red}{{\big(-(x-x_0)/\delta \big)^2}\over{2!}}} }\\ &~~~~~~~~~~~~~~~\color{red} +{ {{\big(-(x-x_0)/\delta \big)^3}\over{3!}}} + \cdots \color{black} \big]\Big]^2 - V_0\\ \end{align}

위 (16)식에서 빨강색 부분이 (12)식을 적용한 부분입니다. 이때 $x-x_0$ 가 1보다 아주 작으므로 이것을 제곱하고 세제곱하는 항들은 무척 크기가 작아지므로 무시가능할 거에요.

그러면 결국 다음과 같이 아주 간단하게 정리가 된답니다.

\tag{17} \begin{align} V(x) &= V_0 \Big({{x-x_0}\over{\delta}} \Big)^2 - V_0\\ &={{V_0}\over{\delta^2}}(x-x_0)^2 - V_0 \end{align}

이것이 뜻하는 것은 복잡한 Morse 위치에너지 함수가 $x_0$ 근처에서 $(x-x_0)$ 의 이차함수로 간단히 표현될 수 있다는 것입니다.

이때 명심하세요. (17)식은 $x$ 가 $x_0$ 로부터 멀어지면 사용할 수 없어요.

아래의 [그림 2]는 $V_0 = 10$ , $x_0 = 5$ , $\delta = 4$ 를 (15)식의 Morse 위치에너지 함수와 (17)식의 테일러 급수 근사식에 대입한 후 그려낸 곡선입니다.

[그림 2] 테일러 급수 전개로 구한 빨강색 곡선이 Mose 포텐셜 함수인 검정색 곡선과 파랑색 사각형 부분에서 매우 일치합니다.

그림 안에 파랑색 사각형으로 표시한 것처럼 $x_0 = 5$ 근처에서 두 곡선이 아주 잘 일치하는 것을 알 수 있어요. 하지만 $x_0$ 로부터 $x$ 가 멀어질수록 오차는 급격히 증가하게 됩니다.

3. 테일러 급수 증명

테일러 급수 유도는 위키백과의 테일러급수에서도 소개하고 있습니다. 거시적인 내용은 위키백과를 참고하면 좋아요. 그러나 구체적인 전개 과정이 궁금한 사람은 아래를 계속 참고하세요.

눈으로 보는것 보다는 노트에 적어가면서 공부하는게 좋아요. 이제부터 시작합니다.

미적분학의 기본 정리에 따르면 아래의 식이 성립합니다.

\tag{1-1} \red{\int_a^x f ^\prime (t) dt }= f(x)-f(a)

이때 빨강색으로 표시한 (1-1)식의 좌변을 아래와 같이 변경하여 표기할 수 있을거에요.

\tag{1-2} \red{\int_a^x f ^\prime (t) dt =\int_a^x \big(-f^\prime (t)\big)\big(-1\big) dt}

그리고 (1-2)식의 우변을 부분적분법으로 적분하면 되는데요. 부분 적분법은 아래의 식을 활용하세요.

\tag{1-3} \int_a^x u(t)v^\prime (t) dt = \Big[u(t)v(t)\Big]_a^x - \int_a^x u^\prime (t) v(t) dt

(1-3)식의 $u(t)$ 를 (1-2)식의 $-f^\prime (t)$ 로, $v^\prime (t)$ 를 $-1$ 로 보시면 됩니다.

\tag{1-4} \begin{align} \red{\int_a^x f ^\prime (t) dt} &\red { = \int_a^x \big(-f^\prime (t)\big)\big(-1\big) dt}\\ &\red{=\Big[-f^\prime (t) (-t+x)\Big]_a^x} \red{-\int_a^x -f^{\prime \prime}(t)(-t+x)dt}\\ &\red{=\Big(-f^\prime(x)(-x+x)\Big) -\Big(-f^\prime(a)(-a+x)\Big) -\int_a^x -f^{\prime \prime}(t)(-t+x)dt}\\ &\red{=(x-a)f^\prime(a)-}\blue{\int_a^x -f^{\prime \prime}(t)(-t+x)dt} \end{align}

위 (1-4)식의 첫번째에서 두번째 줄로 바뀔때 -1을 $t$ 에 대해 적분하여 $(-t+x)$ 로 하였습니다. 이때 $x$ 는 적분상수로서, 적분구간의 상한인 $x$ 와 동일하게 설정함으로써 세번째 줄의 첫번째 항을 0으로 만들 수 있습니다.

적분 결과 (1-4)식의 마지막 줄 파랑색 글자와 같이 또 다른 적분이 나오는 것을 알 수 있습니다. 이번에는 파랑색으로 표기한 적분을 해보도록 하죠. 위에서 시도했던 부분적분법을 다시 한번 더 적용합니다.

\tag{1-5} \begin{align} \blue{\int_a^x - f^{\prime \prime}(t)(-t+x) dt} & \blue{= \int_a^x \Big(f^{\prime \prime }(t)(-t+x)\Big)\Big(-1\Big)dt}\\ &\blue{=\Big[\Big(f^{\prime \prime} (t)(-t+x)\Big)\Big(-t+x\Big)\Big]_a^x }\\ &~~~~~~~~~~~~~\blue{-\int_a^x \Big(f^{\prime \prime \prime}(t)(-t+x)+f^{\prime \prime}(t)(-1)\Big)\Big(-t+x\Big)dt}\\ &\blue{=\Big(f^{\prime \prime}(x)(-x+x)(-x+x)\Big) - \Big(f^{\prime \prime}(a)(-a+x)(-a+x)\Big)}\\ &~~~~~~~~~~~~~\blue{-\int_a^x f^{\prime \prime \prime}(t)(-t+x)^2-f^{\prime \prime}(t)(-t+x)dt}\\ &\blue{=-f^{\prime\prime}(a)(x-a)^2}\\ &~~~~~~~~~~~~~\blue{-\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt + \int_a^x f^{\prime\prime}(t)(-t+x)dt} \end{align}

이때 (1-5)식의 우변에 있는 가장 끝 항을 좌변으로 이항하면 다음의 식이 성립합니다.

\tag{1-6} \begin{align} \blue{2\int_a^x -f^{\prime \prime}(t)(-t+x)dt = -f^{\prime\prime}(a)(x-a)^2 - \int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt} \end{align}

\tag{1-7} \begin{align} \blue{\int_a^x -f^{\prime \prime}(t)(-t+x)dt = -{{(x-a)^2}\over{2}}f^{\prime\prime}(a) - {{1}\over{2}}} \blue{\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt} \end{align}

구해진 (1-7)식을 (1-4)식의 파랑색 부분에 대입하면 아래와 같습니다.

\tag{1-8} \begin{align} \red{\int_a^x f ^\prime (t) dt} & \red { =(x-a)f^{\prime}(a)-\Big(-{{(x-a)^2}\over{2}}f^{\prime\prime}(a)-{{1}\over{2}}\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt \Big)}\\ &\red{=(x-a)f^{\prime}(a)+{{(x-a)^2}\over{2}}f^{\prime\prime}(a)+{{1}\over{2}}}\color{blue}{\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt } \end{align}

그런데 (1-8)식에서 진한 파랑색으로 표시한 것과 같이 적분이 또 나왔습니다. 부분적분법을 또 적용해보세요.

\tag{1-9} \begin{align} \color{blue}\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt &\color{blue}= \int_a^x \Big(-f^{\prime\prime\prime}(t)(-t+x)^2 \Big) \Big(-1\Big) dt\\ & \color{blue}=\Big[ \Big(-f^{\prime\prime\prime}(t)(-t+x)^2 \Big)\Big(-t+x\Big) \Big]_a^x\\ &\color{blue}~~~~~~-\int_a^x \Big(-f^{\prime\prime\prime\prime}(t)(-t+x)^2 +\big(- f^{\prime\prime\prime}(t)(2)(-t+x)(-1)\big)\Big)\\ &\color{blue}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\Big(-t+x\Big)dt\\ &\color{blue}=\Big( \big(-f^{\prime\prime\prime}(x)(-x+x)^3 \big) - \big(-f^{\prime\prime\prime}(a)(-a+x)^3 \Big)\\ &\color{blue} ~~~~~~-\int_a^x \Big(-f^{\prime\prime\prime\prime}(t)(-t+x)^3 \Big)+\Big(-f^{{\prime\prime\prime}} (t)(-t+x)^2 (-2)\Big)dt\\ &\color{blue} =f^{\prime\prime\prime}(a) (x-a)^3 \\ &\color{blue} ~~~~~~+\int_a^x f^{\prime\prime\prime\prime}(t)(-t+x)^3 dt-2\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt\\ \end{align}

이때 (1-9)식의 우변에 있는 가장 끝 항을 좌변으로 이항하면 다음의 식이 성립합니다.

\tag{1-10} \color{blue}3\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2 dt = f^{\prime\prime\prime}(a)(x-a)^3 + \int_a^x f^{\prime\prime\prime\prime}(t)(-t+x)^3 dt

\tag{1-11} \color{blue}\int_a^x f^{\prime\prime\prime}(t)(-t+x)^2dt = {{(x-a)^3}\over{3}}f^{\prime\prime\prime}(a)+{{1}\over{3}}\int_a^x f^{\prime\prime\prime\prime}(t)(-t+x)^3 dt

구해진 (1-11)식을 (1-8)식의 진한 파랑색 부분에 대입하면 아래와 같습니다.

\tag{1-12} \begin{align} \color{red}{\int_a^x f ^\prime (t) dt} &\color{red}{=(x-a)f^{\prime}(a)+{{(x-a)^2}\over{2}}f^{\prime\prime}(a)}\\ &~~~~~~\color{red}+{{1}\over{2}}\Big({{(x-a)^3}\over{3}} f^{\prime\prime\prime}(a) + {{1}\over{3}}\int_a^x f^{\prime\prime\prime\prime}(t)(-t+x)^3 dt\Big)\\ &\color{red} = (x-a)f^{\prime}(a) + {{(x-a)^2}\over{2 \times1}}f^{\prime\prime}(a)+{{(x-a)^3}\over{3 \times 2\times1}}f^{\prime\prime\prime}(a)+\cdots \end{align}

최종적으로 (1-12)식을 (1-1)식의 좌변에 대입하면 아래와 같습니다.

\tag{1-13} \begin{align} \color{black}{\int_a^x f ^\prime (t) dt} &\color{black}=f(x)-f(a)\\ \color{black} (x-a)f^{\prime}(a) + {{(x-a)^2}\over{2 \times1}}f^{\prime\prime}(a)+{{(x-a)^3}\over{3 \times 2\times1}}f^{\prime\prime\prime}(a)+\cdots \color{red}&= f(x)-f(a) \end{align}

결국 $f(x)$ 는 다음과 같습니다.

\tag{1-14} \begin{align} \color{black} f(x)=f(a)+ (x-a)f^{\prime}(a) + {{(x-a)^2}\over{2 !}}f^{\prime\prime}(a)+{{(x-a)^3}\over{3!}}f^{\prime\prime\prime}(a)+\cdots \color{red} \end{align}

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 13 Average: 4.8]

테일러 급수 증명과 활용 사례