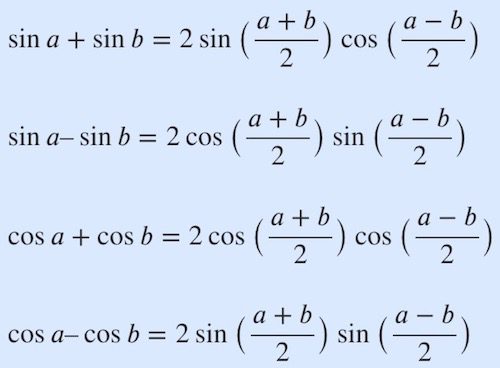Last Updated on 2025-07-19 by BallPen
삼각함수 합 또는 차를 곱으로 바꾸는 공식을 유도해 봐요.
삼각함수 합 또는 차를 곱으로 바꾸는 공식입니다.
\begin{align*}
&\sin a + \sin b = 2 \sin \big({{a+b}\over{2}}\big) \cos\big({{a-b}\over{2}}\big)\\[10pt]
&\sin a – \sin b = 2 \cos \big({{a+b}\over{2}}\big) \sin\big({{a-b}\over{2}}\big)\\[10pt]
&\cos a + \cos b = 2 \cos \big({{a+b}\over{2}}\big) \cos\big({{a-b}\over{2}}\big)\\[10pt]
&\cos a – \cos b = 2 \sin \big({{a+b}\over{2}}\big) \sin\big({{a-b}\over{2}}\big)\\
\end{align*}
이 글에서는 위 삼각함수 공식들을 유도해 보겠습니다. 혹시 삼각함수 곱을 합 또는 차로 바꾸는 공식을 알고 싶으면 링크를 클릭해 주세요.
1. 삼각함수 합 또는 차를 곱으로 바꾸는 공식
1-1. 첫 번째 공식
첫 번째 공식을 유도하기 위해서는 삼각함수 곱을 합으로 바꾸는 공식 중 아래의 공식부터 시작해야 해요.
\begin{align}
\tag{1}
\sin \alpha \cos \beta = {1 \over 2} \big\{ \sin (\alpha+\beta) + \sin (\alpha – \beta) \big\}
\end{align}
이때 위 식에서 \(\alpha\)와 \(\beta\)가 다음과 같다고 생각해봐요.
\begin{align}
\tag{2}
\alpha = {{a+b}\over{2}},~~~~\beta = {{a-b}\over{2}}
\end{align}
그리고 (2)식을 (1)식에 대입해 봐요. 다음과 같습니다.
\begin{align}
\tag{3}
\sin\big( {{a+b}\over{2}} \big) \cos \big({{a-b}\over{2}}\big) &= {1 \over 2} \big\{ \sin \big( {{a+b}\over{2}} + {{a-b}\over{2}}\big) \\
&~~~~~~~~~~~~~~~~~~~+ \sin \big( {{a+b}\over{2}} – {{a-b}\over{2}} \big) \big\}
\end{align}
위 식의 양변을 2로 곱하고 정리하면 다음과 같아요.
\begin{align}
\tag{4}
2\sin\big( {{a+b}\over{2}} \big) \cos \big({{a-b}\over{2}}\big) = \sin a + \sin b
\end{align}
마지막으로 위 식의 양변을 서로 바꾸면 다음의 공식이 성립합니다.
\begin{align}
\tag{5}
\sin a + \sin b=2\sin\big( {{a+b}\over{2}} \big) \cos \big({{a-b}\over{2}}\big)
\end{align}
1-2. 두 번째 공식
두 번째 공식을 유도하기 위해서는 삼각함수 곱을 합으로 바꾸는 공식 중 아래의 공식부터 시작해야 해요.
\begin{align}
\tag{6}
\cos \alpha \sin \beta = {1 \over 2} \big\{ \sin (\alpha+\beta) – \sin (\alpha – \beta) \big\}
\end{align}
이때 위 식에서 \(\alpha\)와 \(\beta\)가 다음과 같다고 생각해봐요.
\begin{align}
\tag{7}
\alpha = {{a+b}\over{2}},~~~~\beta = {{a-b}\over{2}}
\end{align}
그리고 (7)식을 (6)식에 대입해 봐요. 다음과 같습니다.
\begin{align}
\tag{8}
\cos \big( {{a+b}\over{2}} \big) \sin \big({{a-b}\over{2}}\big) &= {1 \over 2} \big\{ \sin \big( {{a+b}\over{2}} + {{a-b}\over{2}}\big) \\
&~~~~~~~~~~~~~~~~~~~- \sin \big( {{a+b}\over{2}} – {{a-b}\over{2}} \big) \big\}
\end{align}
위 식의 양변을 2로 곱하고 정리하면 다음과 같아요.
\begin{align}
\tag{9}
2\cos\big( {{a+b}\over{2}} \big) \sin \big({{a-b}\over{2}}\big) = \sin a – \sin b
\end{align}
마지막으로 위 식의 양변을 서로 바꾸면 다음의 공식이 성립합니다.
\begin{align}
\tag{10}
\sin a – \sin b=2\cos\big( {{a+b}\over{2}} \big) \sin \big({{a-b}\over{2}}\big)
\end{align}
1-3. 세 번째 공식
세 번째 공식을 유도하기 위해서는 삼각함수 곱을 합으로 바꾸는 공식 중 아래의 공식부터 시작해야 해요.
\begin{align}
\tag{11}
\cos \alpha \cos \beta = {1 \over 2} \big\{ \cos (\alpha+\beta) + \cos (\alpha – \beta) \big\}
\end{align}
이때 위 식에서 \(\alpha\)와 \(\beta\)가 다음과 같다고 생각해봐요.
\begin{align}
\tag{12}
\alpha = {{a+b}\over{2}},~~~~\beta = {{a-b}\over{2}}
\end{align}
그리고 (12)식을 (11)식에 대입해 봐요. 다음과 같습니다.
\begin{align}
\tag{13}
\cos \big( {{a+b}\over{2}} \big) \cos \big({{a-b}\over{2}}\big) &= {1 \over 2} \big\{ \cos \big( {{a+b}\over{2}} + {{a-b}\over{2}}\big) \\
&~~~~~~~~~~~~~~~~~~~+ \cos \big( {{a+b}\over{2}} – {{a-b}\over{2}} \big) \big\}
\end{align}
위 식의 양변을 2로 곱하고 정리하면 다음과 같아요.
\begin{align}
\tag{14}
2\cos\big( {{a+b}\over{2}} \big) \cos \big({{a-b}\over{2}}\big) = \cos a + \cos b
\end{align}
마지막으로 위 식의 양변을 서로 바꾸면 다음의 공식이 성립합니다.
\begin{align}
\tag{15}
\cos a + \cos b=2\cos\big( {{a+b}\over{2}} \big) \cos \big({{a-b}\over{2}}\big)
\end{align}
1-4. 네 번째 공식
네 번째 공식을 유도하기 위해서는 삼각함수 곱을 합으로 바꾸는 공식 중 아래의 공식부터 시작해야 해요.
\begin{align}
\tag{16}
\sin \alpha \sin \beta = {1 \over 2} \big\{ \cos (\alpha+\beta) – \cos (\alpha – \beta) \big\}
\end{align}
이때 위 식에서 \(\alpha\)와 \(\beta\)가 다음과 같다고 생각해봐요.
\begin{align}
\tag{17}
\alpha = {{a+b}\over{2}},~~~~\beta = {{a-b}\over{2}}
\end{align}
그리고 (17)식을 (16)식에 대입해 봐요. 다음과 같습니다.
\begin{align}
\tag{18}
\sin \big( {{a+b}\over{2}} \big) \sin \big({{a-b}\over{2}}\big) &= {1 \over 2} \big\{ \cos \big( {{a+b}\over{2}} + {{a-b}\over{2}}\big) \\
&~~~~~~~~~~~~~~~~~~~- \cos \big( {{a+b}\over{2}} – {{a-b}\over{2}} \big) \big\}
\end{align}
위 식의 양변을 2로 곱하고 정리하면 다음과 같아요.
\begin{align}
\tag{19}
2\sin\big( {{a+b}\over{2}} \big) \sin \big({{a-b}\over{2}}\big) = \cos a – \cos b
\end{align}
마지막으로 위 식의 양변을 서로 바꾸면 다음의 공식이 성립합니다.
\begin{align}
\tag{20}
\cos a – \cos b=2\sin\big( {{a+b}\over{2}} \big) \sin \big({{a-b}\over{2}}\big)
\end{align}