변수분리형 미분방정식 풀이 방법

Last Updated on 2024-03-18 by BallPen

대수적 조작을 통해 변수의 분리가 가능한 변수분리형 미분방정식의 해법을 알아보겠습니다.

변수분리형 미분방정식 풀이 방법과 몇가지 예제를 이번 글에서 다룹니다.

혹시라도 여기서 나오는 용어와 내용이 잘 이해가 가지 않으면 미분방정식 기초에 대한 이전 글을 참조해 주세요.

아울러 미분방정식 해의 종류에 대한 이전 글도 도움이 될거에요.

그럼 이제 시작해보겠습니다. 아래는 이번 글의 목차입니다.

1. 변수분리형 미분방정식

아래의 식(1)과 (2)는 미분방정식입니다.

여기서 f(x)는 x에만 의존하는 함수이고, f(y)는 y에만 의존하는 함수를 뜻합니다.

\begin{align}
{{dy}\over{dx}} &= f(x) g(y)\\
{{dy}\over{dx}} &= {{f(x)}\over{g(y)}}
\end{align}

이 두 미분방정식의 특징은 x와 y를 서로 분리하여 대수적으로 정리할 수 있다는 거에요.

우선 (1)식을 정리해 보겠습니다. 좌변은 y와 관련된 것으로, 우변은 x와 관련된 것으로 나눌 수 있어요.

\tag{3}
{1 \over g(y)} dy = f(x)dx

그리고는 양변을 적분하면 다음과 같이 쓸 수 있습니다.

\tag{4}
\int {1 \over g(y)}dy = \int f(x) dx

이러한 과정을 통해 x에 의존하는 함수 y를 구할 수 있게 되는데요.

이것이 곧 (1)식에 주어진 미분방정식의 해입니다.

이와 같이 변수를 좌변과 우변으로 서로 분리시킨 후 양변을 적분하여 풀수 있는 미분 방정식을 ‘변수분리형 미분방정식’이라고 합니다.

이제는 (2)식에 대해서도 변수를 분리한 후, 양변을 적분해 보겠습니다.

\tag{5}
g(y) dy = f(x) dx

\tag{6}
\int g(y) dy = \int f(x)dx

일반적으로 (1)식보다는 (2)식의 형태로 이루어진 변수분리형 미분방정식의 풀이가 쉽답니다.

몇가지 예제를 다루어 보겠습니다.

2. 변수분리형 미분방정식 예제

[예제1] (1)식의 유형

\tag{7}
\color{blue}y^\prime = 1+y^2

[풀이]

이 미분방정식은 미분기호 표현법에 따라 다음과 같이 바꾸어 쓸 수 있습니다.

\tag{8}
\begin{align}
\color{black}{{dy}\over{dx}} = 1+ y^2\\
\end{align}

그리고는 변수를 분리합니다.

\tag{9}
{{1}\over{1+y^2}}dy = dx

이제 양변을 적분하면 되는데요. 아래와 같이 표현할 수 있습니다.

\tag{10}
\int {{1}\over{1+y^2}}dy = \int dx

(10)식의 좌변을 적분하기 위해 적분표에서 볼 수 있는 다음의 관계를 활용합니다.

\tag{11}
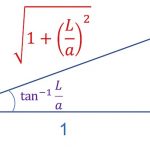
\color {red}\int {1 \over {a^2 + x^2}} dx = {1 \over a} \tan^{-1} {{x}\over{a}}+C

그러므로 (10)식의 좌변은 (11)식에서 a는 1, x는 y인 경우로 보면 됩니다.

결국 (10)식의 좌변과 우변을 적분한 결과는 다음과 같아요.

\tag{12}
\tan^{-1} y + C_1 = x + C_2

(12)식에서 C_1과 C_2는 모두 적분상수입니다. 상수끼리의 연산은 어차피 또다른 상수일 뿐이므로 이 둘 사이의 연산을 하나로 묶어 C로 표현하면 간결해서 좋습니다.

\tag{13}
\begin{align}
\tan^{-1} y &= x+(C_2 - C_1)\\
&=x + C
\end{align}

따라서 (7)식으로 주어진 미분방정식의 일반해는 다음과 같이 쓸 수 있습니다.

\tag{14}
y = \tan (x+C)

[예제2] (2)식의 유형

\tag{15}
\color{blue}9y y^{\prime} +4x =0

[풀이]

이 미분 방정식은 다음과 같이 표현을 바꿀 수 있어요.

\tag{16}
9y{{dy}\over{dx}} + 4x = 0

좌변은 y끼리, 우변은 x끼리 모여지도록 변수를 분리해 보세요.

\tag{17}
 9y dy= -4x dx

그리고는 양변을 적분합니다.

\tag{18}
9\int ydy = -4\int xdx

적분 결과는 다음과 같습니다.

\tag{19}
\begin{align}
&9\Big( {{y^2}\over{2}} + C_1\Big) = -4\Big( {{x^2}\over{2}} + C_2 \Big)\\
&{{9}\over{2}} y^2 = -2 x^2 + \big(-4C_2 - 9C_1 \Big)\\
&y^2 = -{{4}\over{9}}x^2 + C 
\end{align}

여기서도 상수끼리의 연산은 또 다른 상수를 만들뿐이므로 상수를 C로 묶었습니다.

최종적으로 (15)식으로 주어진 미분방정식의 일반해는 다음과 같습니다.

\tag{20}
y = \Big( -{{4}\over{9}} x^2 + C \Big)^{1/2}

이것이 올바른 해인지의 여부를 확인하고 싶으면 (20)식을 (15)식에 대입해서 항등관계가 만족하는 지를 확인해보면 됩니다.

3. 변수분리형 미분방정식 활용 분야

3.1 방사성물질의 붕괴율

방사성 물질이란 불안정한 원자핵이 알파선, 베타선, 감마선, 전자선, X선 등의 방사선을 방출하면서 안정한 핵으로 변환되는 물질을 말합니다.

이와 같이 불안정한 상태의 원자핵이 안정한 상태로 바뀌는 것을 ‘방사성 물질이 붕괴한다’고 말합니다.

또한 어느 방사성 물질이 있을 때 단위시간당 붕괴율은 방사성 물질의 현재 양에 비례합니다. 즉, 방사성 물질의 양이 많으면 빠른 비율로 붕괴하고, 방사성 물질의 양이 적으면 상대적으로 느린 비율로 붕괴하는 것이죠.

이것은 현재 온도가 높을수록 빠른 기울기로 식고, 현재 온도가 낮을수록 느린 기울기로 식는 것과 같은 이치입니다.

이를 식으로 표현하면 다음과 같습니다. 이때 t는 시간, y는 방사성 물질의 양이며, k는 상수입니다.

\tag{21}
{{dy}\over{dt}} = ky

예를 들어 방사성 물질인 라듐이 100 mg 있다고 생각해보세요. 임의의 시간 t~\mathrm{s}후에 라듐의 양은 얼마가 남아 있을까요? 단, k=-1.4 \times 10^{-11} / \mathrm{s}입니다.

(21)식의 미분방정식을 풀면 시간 t의 함수로서의 라듐의 양 y를 표현하는 식을 얻을 수 있습니다.

[일반해]

우선 변수를 분리합니다. 이때 k는 상수이므로 어느 쪽에 두어도 상관없습니다. 저는 우변에 두겠습니다.

\tag{22}
{{1}\over{y}} dy = k dt

이제는 양변을 적분하세요.

\tag{23}
\int {{1}\over{y}}dy = k\int dt

나머지 풀이 과정은 다음과 같습니다.

\tag{24}
\begin{align}
&\ln y + C_1 = k(t + C_2)\\
&\ln y = kt+(k C_2 - C_1)\\
&\ln y = kt + C
\end{align}

최종적으로 위 식의 가장 마지막 줄 양변에 e을 취하면 일반해를 구할 수 있어요.

\tag{25}
\begin{align}
y &= e^{kt+C}\\
& = e^C e^{kt}\\
&=A e^{kt}
\end{align}

위 일반해에서 적분상수 C에 exponential을 취한 e^{C}도 또 하나의 상수가 될 뿐이므로 그 값을 A로 표기한 것입니다.

(25)식에 적절한 초기값을 대입하면 상수 A를 구할 수 있게 되는데요. 그러한 해를 특수해라고 합니다.

[특수해]

예를 들어 초기값이 t=0에서 y_0=100~ \mathrm{mg}이라고 해보겠습니다.

이 초기값을 식(25)의 일반해에 대입해 보세요.

\tag{26}
\begin{align}
&100 = A e^{0}\\
&A = 100
\end{align}

초기값을 통해 상수 A가 100의 값을 갖는다는 것을 알았습니다. 그리고 이 수치는 y_0임을 알 수 있어요.

그러므로 (21)식에 주어진 미분방정식의 특수해는 다음과 같습니다.

\tag{27}
\begin{align}
y & = y_0 e^{kt}\\
&= 100 e^{kt}\\
&=100 e^{(-1.4 \times10^{-11}) t }
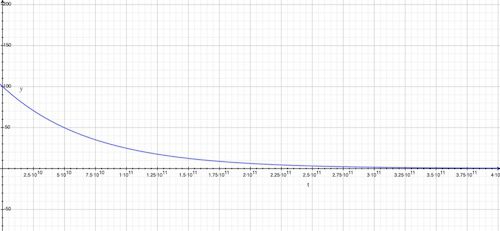
\end{align}

아래 [그림 1]은 (27)식에 주어진 특수해를 그래프로 그려본 것입니다. 라듐의 양이 최초 100 mg으로부터 시간에 따라 지수적으로 감소하는 것을 알 수 있어요.

3.2 방사성 물질의 반감기

불안정한 방사성 물질의 원자핵은 붕괴과정을 거쳐 안정된 원자핵으로 변하게 된다고 말씀드렸습니다. 여기서 중요한 것은 방사성 물질이 일시에 한꺼번에 모두 안정된 원자핵으로 변하지 않습니다.

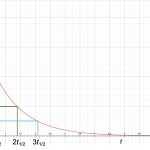
시간을 두고 방사성 물질이 점점 줄어들면서 안정된 핵으로 바뀌게 되는데요. 이때 방사성 물질의 양이 절반으로 줄어드는데 걸리는 시간을 ‘반감기(half-life)‘라고 부릅니다.

따라서, 반감기의 시간이 지나면 방사성 물질의 양이 최초의 양 y_0보다 절반인 {{y_0}\over{2}}로 줄고, 다시 반감기가 지나면 {{y_0}\over{2}}의 절반인 {{y_0}\over{4}}로 줄게 됩니다.

따라서 (27)식의 첫째줄을 약간 변형하면 다음과 같이 표현할 수 있습니다. 이때 t_{1/2}는 반감기의 시간을 의미합니다.

\tag{28}
{{y_0}\over{2}} =y_0 e^{k t_{1/2}}

식에서 y_0를 약분하고 양변에 \ln을 취한 후, t_{1/2}에 대해 정리하면 다음의 결과를 얻습니다.

\tag{29}
\begin{align}
{\cancel{y_0}\over{2}} &=\cancel {y_0} e^{k t_{1/2}}\\
{1 \over 2} &= e^{k t_{1/2}}\\
\ln {1 \over 2} &= k t_{1/2}\\
t_{1/2} &={1 \over k } \ln 0.5 
\end{align}

문제에 주어진 상수 k를 반영하여 반감기 t_{1/2}를 구하면 아래와 같습니다.

\tag{30}
\begin{align}
t_{1/2} &= {1 \over{-1.4 \times 10^{-11}/ \mathrm{s}}}\ln 0.5\\
&=4.95 \times 10^{10} ~\mathrm s
\end{align}

[그림 1]에서 볼수 있는 것처럼 100 mg의 절반인 50 mg이 남게 되는 시간은 4.95 \times 10^{10} ~\mathrm{s}입니다.

이정도의 시간은 몇 년에 해당할까요? 계산해보면 아래와 같이 약 1600년 정도가 됩니다.

\tag{31}
\begin{align}
t_{1/2} &={{4.95 \times 10^{10}~\mathrm{s}}\over{3600~{\mathrm{s/h}\times24~{\mathrm{h/day}\times365~\mathrm{day/year}}}}} \\
&=1570~\mathrm{year}\\
&\approx1600 ~\mathrm{year}
\end{align}

아주 오랜 시간이 걸리는군요.

Related posts.

확장된 변수분리형 미분방정식 풀이 방법 반감기(half-life) 뜻과 공식 유도 연금 월평균 수령액. 10년전 35만원, 그럼 지금은? 통계 용어 주요 개념에 대한 인용 자료(가계금융복지조사) 창업 기업 수에 대한 업종별 최근 통계를 확인해 보세요 두배각 공식 푸리에 급수 전개 곱의 미분