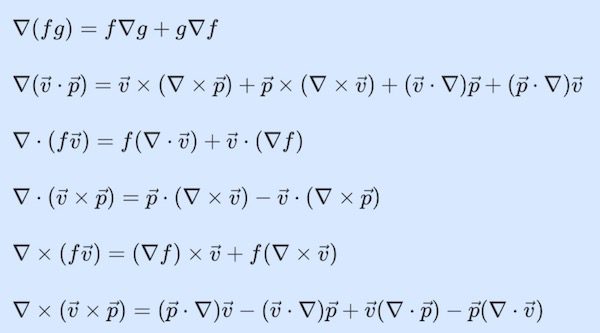Last Updated on 2025-08-29 by BallPen
벡터 미분 연산자를 이용한 일계 미분의 몇가지 곱셈 규칙을 알아 봐요.
일계 미분 곱셈 규칙 몇가지를 알아 봐요. 전자기학 등을 공부할 때 자주 등장하는 규칙들이에요.
참고로 몇가지 이계 미분 곱셈 규칙도 있으니 이것이 궁금하면 링크를 클릭하시기 바랍니다.
벡터 미분 연산자(또는 델연산자)가 사용된 일계 미분 곱셈 규칙은 다음과 같아요. 여기서 f와 g는 스칼라 함수이고 \vec v와 \vec p는 벡터함수입니다.
\begin{align}
&\nabla(fg) = f\nabla g + g \nabla f\\[10pt]
&\nabla(\vec v \cdot \vec p) = \vec v \times (\nabla \times \vec p) + \vec p \times (\nabla \times \vec v) + (\vec v \cdot \nabla)\vec p + (\vec p \cdot \nabla)\vec v\\[10pt]
&\nabla \cdot (f \vec v) = f(\nabla \cdot \vec v) + \vec v \cdot (\nabla f)\\[10pt]
&\nabla \cdot (\vec v \times \vec p) = \vec p \cdot (\nabla \times \vec v)-\vec v \cdot (\nabla \times \vec p)\\[10pt]
&\nabla \times (f \vec v) = (\nabla f) \times \vec v + f(\nabla \times \vec v)\\[10pt]
&\nabla \times (\vec v \times \vec p) = (\vec p \cdot \nabla) \vec v - (\vec v \cdot \nabla)\vec p + \vec v(\nabla \cdot \vec p) - \vec p (\nabla \cdot \vec v)
\end{align}흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 1 Average: 5]