복소수(complex numbers)

BallPen · 2024-01-26T14:41:22+09:00

복소수(complex numbers)는 실수와 허수가 결합된 수 체계입니다. 복소수는 x+iy로 주로 표현되나 오일러 공식을 통해 극형식으로 나타낼 수도 있어요. 복소수의 사칙연산, 복소 삼각함수, 복소 쌍곡선함수, 복소 로그 함수에 대해 설명합니다.

Last Updated on 2024-01-26 by BallPen

복소수의 다양한 표현법과 연산법, 그리고 관련 공식들을 알아봐요.

복소수(complex numbers)란 실수와 허수가 결합된 수 체계입니다. 기호로 쓰면 다음과 같아요.

\tag{D1} x+iy

여기서 $x$ 는 실수부(real part)라고 부르며, 허수 $iy$ 중 $y$ 를 허수부(imaginary part)라고 부릅니다.

이번 글에서는 복소수를 표현하는 다양한 방식과 복소수의 연산, 그리고 여러 관련 공식들을 알아보겠습니다.

볼펜을 잡고 하나씩 하나씩 직접 정리하며 풀어보세요.

아래는 이번 글의 목차입니다.

1. 복소수

1-1. 복소수의 표현

복소수는 복소 평면(complex plane)에서 표현될 수 있습니다. 여기서 복소 평면이란 복소수의 크기와 위치를 표현하는 특별한 평면 공간을 말해요.

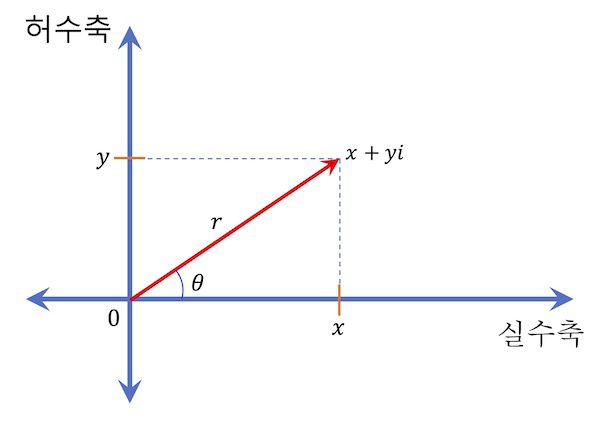
실수는 실수선이라 불리는 가로선 위에 모든 실수들이 배치되는 것에 비해 복소수는 복소 평면위에 배치돼요. 아래 [그림 1]은 복소평면을 나타낸 것입니다.

복소 평면의 가로축은 실수축이고 세로축은 허수축이에요. 이때 복소수의 실수부가 $x$ 이고 허수부가 $y$ 일때 복소수 $z$ 는 아래 (1-1)식과 같이 표현됩니다.

\tag{1-1} z = x + iy

한편 [그림 1]을 보면 복소수 $z$ 의 실수부는 $x = r \cos \theta$ 이고 허수부는 $y=r \sin \theta$ 에요.

따라서 (1-1)식은 다음과 같이 바꾸어 표현할 수도 있어요. 이러한 형태를 복소수의 극형식(polar form)이라고 부릅니다.

\tag{1-2} \begin{align} z &= x+iy\\ &=r \cos \theta + ir\sin \theta\\ &=r(\cos \theta + i\sin \theta) \end{align}

1-2. 복소수의 크기

복소수는 보통 (1-1)식과 (1-2)식으로 표현하는데요. 그 복소수의 크기 $|z|$ 는 [그림 1]에서 빨강색 화살표의 길이 $r$ 를 의미해요.

그래서 복소수의 실수부 $x$ 와 허수부 $y$ 를 피타고라스(Pythagoras) 정리에 대입하면 다음과 같이 그 크기 $|z|$ 를 구할 수 있어요.

\tag{1-3} \begin{align} |z| &= \sqrt{x^2 + y^2}\\[5pt] &=\sqrt{r^2\cos^2 \theta + r^2 \sin^2 \theta}\\[5pt] &=r\sqrt{\cos^2 \theta + \sin^2 \theta}\\[5pt] &=r \end{align}

한편 복소수의 크기는 켤레복소수(complex conjugate)를 이용해 복소수를 실수화하는 방식으로도 구할 수 있어요.

이번에는 그 방법을 알려드릴게요.

어떤 복소수를 $z=x+iy$ 라 할 때 켤레복소수는 $\bar z = x- iy$ 로 정의됩니다. 따라서 켤레복소수는 허수부 $y$ 값의 부호만 바뀌므로 [그림 1]에 있는 화살표가 $x$ 축 대칭으로 바뀌는 것을 기하학적으로 상상하면 됩니다.

켤레복소수는 복소공액이라고 불리기도 해요.

그렇다면 복소수의 크기를 어떻게 구할 수 있을까요? 바로 복소수와 그 켤레복소수를 서로 곱하면 됩니다. 그 결과를 살펴보면 아래 (1-4)식과 같아요.

\tag{1-4} \begin{align} z \bar z &= (x+iy)(x-iy)\\ &=(x)^2 - ixy+ixy - (iy)^2\\ &=\color{blue}x^2 + y^2\\ &=|z|^2 \end{align}

위 식의 세번째 줄은 (1-3)식 첫번째 줄의 양변을 제곱한 것과 같아요. 결국 복소수와 그 켤레복소수를 곱하면 복소수 크기를 제곱한 값과 같습니다.

그 관계를 다시 쓰면 다음과 같아요.

\tag{1-5} r=|z| = \sqrt{z \bar z}

2. 오일러 공식(Euler’s formula)

테일러급수는 어떤 함수를 다항식의 형태로 표현하는 방법을 말해요. 그중에서 $\sin \theta$ , $\cos \theta$ , $e^{\theta}$ 를 전개해보면 다음과 같아요.

\tag{2-1} \begin{align} &\sin \theta = \theta - {{\theta^3}\over{3 !}} + {{\theta^5}\over{5!}}- \cdots\\[10pt] &\cos \theta = 1 - {{\theta^2}\over{2!}} + {{\theta^4}\over{4!}}-\cdots\\[10pt] &e^\theta = 1 + \theta + {{\theta^2}\over{2!}} +{{\theta^3}\over{3!}} + \cdots \end{align}

이때 세번째 줄에 있는 $e^\theta$ 를 $e^{i\theta}$ 로 변경하여 정리해보면 다음이 됩니다.

\tag{2-2} \begin{align} e^{i \theta} &= 1+(i\theta) + {{(i\theta)^2}\over{2!}} + {{(i \theta)^3}\over{3!}} + {{(i \theta)^4}\over{3!}}+\cdots\\[10pt] &=1+i\theta - {{\theta^2}\over{2!}} - {{ i\theta^3}\over{3!}} + {{ \theta^4}\over{4!}}+{{ i\theta^5}\over{5!}}+\cdots\\[10pt] &=\Big(1 - {{\theta^2}\over{2!}} + {{\theta^4}\over{4!}}-...\Big)+i\Big( \theta - {{\theta^3}\over{3 !}} + {{\theta^5}\over{5!}}- \cdots\Big)\\[10pt] &=\cos \theta + i \sin \theta\\[10pt] \end{align}

결국 $e^{i\theta}$ 는 다음과 같이 표현됩니다. 이 식을 오일러 공식이라고 불러요.

\tag{2-3} e^{\pm i \theta} = \cos \theta \pm i \sin \theta

위식에서 $\theta$ 는 [그림 1]처럼 기준축으로부터의 회전 각도인 ‘위상’을 의미해요. 때로는 위상을 ‘편각’이라고 부르기도 합니다.

그런데 오일러 공식을 잘 보면 (1-2)식 $z=r(\cos \theta + i \sin \theta)$ 의 괄호 안과 같다는 것을 알 수 있어요.

따라서 오일러 공식을 이용해 복소수 $z$ 를 극형식으로 표현해보면 다음과 같아요.

\tag{2-4} z =x\pm iy= r(\cos \theta \pm i \sin \theta)=r e^{\pm i\theta}

복소수를 표현하는 다양한 방식이 있음을 알 수 있어요.

3. 복소수 연산

3-1. 복소수의 덧셈과 뺄셈

두 복소수를 더하고 빼는 방법은 다음과 같아요. 실수부는 실수부끼리, 허수부는 허수부끼리 더해주거나 빼주면 됩니다.

\tag{3-1} (x_1 + iy_1) \pm(x_2+iy_2)= (x_1 \pm x_2) + i(y_1 \pm y_2)

[예제1]

(3+i4)와 (5+i6)의 두 복소수를 합하여라.

(sol) 위 (3-1)식을 적용하여 계산하면 됩니다.

\tag{ex-1} (3+i4)+(5+i6) = (3+5)+i(4+6) = 8+i10

만일 두 복소수를 빼고 싶다면 다음과 같이 계산하세요.

\tag{ex-2} (3+i4)-(5+i6) = (3-5)+i(4-6) = -2-i2

3-2. 복소수의 곱

두 복소수의 곱셈은 서로 전개하여 구하거나 다음의 관계를 활용하면 됩니다.

복소수 $z_1 = r_1 e^{i \theta_1}$ 과 $z_2 = r_2 e^{i \theta_2}$ 가 있어요. 이 두 복소수를 곱해 봐요.

\tag{3-2} \begin{align} z_1 \cdot z_2 &= r_1 e^{i\theta_1} \cdot r_2e^{i\theta_2} \\[5pt] &=r_1 r_2 e^{i(\theta_1 + \theta_2)} \end{align}

위 식과 같이 두 복소수를 곱하면 복소수 크기는 서로 곱해지고 위상은 서로 합해지는 특성이 있어요.

[예제2]

(3+i4)와 (3+i4)의 두 복소수를 곱하여라.

(sol) 두개의 해법이 있습니다. 하나는 전개하여 구하는 방법과 다른 하나는 (3-2)식을 활용하는 거에요.

우선 전개하는 방법으로 구해봐요.

\tag{ex-3} \begin{align} (3+i4)(3+i4) &= 9+i12+i12+16i^2\\ &=9+i24-16\\ &=-7+i24 \end{align}

이번에는 (3-2)식을 적용해봐요. 이때 (3+i4)의 위상은 $\cos \theta = {{x}\over{r}}$ 이므로 $\theta = \cos^{-1} {{x}\over{r}}$ 입니다.

\tag{ex-4} \begin{align} (3+i4)(3+i4) &= \big(\sqrt{3^2 + 4^2}e^{i\cos^{-1}{{3}\over{\sqrt{3^2 + 4^2}}}}\Big) \big(\sqrt{3^2 + 4^2}e^{i\cos^{-1}{{3}\over{\sqrt{3^2 + 4^2}}}}\Big)\\ &=5e^{i53.1^{\circ}}5e^{i53.1^{\circ}}\\ &=25e^{i106.2^{\circ}}\\ &=25(\cos {106.2^{\circ}} + i\sin 106.2^{\circ})\\ &=-7+i24 \end{align}

두 결과가 서로 같다는 것을 알 수 있어요.

3-3. 복소수의 나눗셈

두 복소수가 분수로 표현된 경우 이를 단일의 복소수로 정리할 필요가 있어요. 그때는 분모에 있는 복소수의 켤레복소수를 분모와 분자에 모두 곱하여 분모를 실수화한 후 정리합니다.

바로 예제를 하나 풀어보겠습니다.

[예제3]

(3+i)를 (2+i)로 나누어라.

(sol) 분모에 있는 복소수의 켤레복소수를 분자와 분모에 모두 곱해줍니다.

\tag{ex-5} \begin{align} {{3+i}\over{2+i}} &= {{(3+i)\color{red}(2-i)}\over{(2+i)\color{red}(2-i)}} \\[10pt] &={{6-i3 + i2 - i^2}\over{2^2 -i^2}}\\[10pt] &={{7-i}\over{4+1}}\\[10pt] &={7 \over 5} - i{1 \over 5} \end{align}

3-4. 복소수의 거듭제곱

복소수 $z=re^{i\theta}$ 의 $n$ 제곱은 다음과 같이 표현할 수 있을거에요.

\tag{3-3} z^n = (re^{i \theta})^n = r^n (e^{in\theta})

이때 (3-3)식의 가운데 항은 다음과 같이도 표현될 수 있어요.

\tag{3-4} z^n = (re^{i \theta})^n = r^n (e^{i \theta})^n = r^n(\cos \theta + i \sin)^n

또한 (3-3)식의 가장 오른쪽 항은 다음 관계도 성립할거에요.

\tag{3-5} \begin{align} z^n = r^n(e^{in \theta}) = r^n (\cos n\theta + i \sin n\theta) \end{align}

이때 (3-3)식에 따라 (3-4)과 (3-5)식은 서로 같아야 하므로 결국 다음 관계가 성립합니다.

\tag{3-6} z^n = r^n(\cos \theta + i \sin \theta)^n = r^n(\cos n \theta + i \sin n \theta)

한편 복소수에 $1 \over n$ 승을 취하면 (3-6)식은 다음과 같이 표현됩니다.

\tag{3-6} z^{1 \over n} = r^{1 \over n}(\cos \theta + i \sin \theta)^{1\over n} = r^{1 \over n}(\cos {\theta \over n} + i \sin {\theta \over n})

[예제4]

8의 세제곱근을 복소수 범위에서 모두 구하여라.

(Sol) 복소수 범위에서 8의 세제곱근은 총 3개의 해가 나옵니다. 일단 8의 세제곱은 $8^{1/3}$ 로 쓸 수 있는데요.

이를 복소수로 확장하기 위해 $8^{1/3} (e^{ix})^{1/3}$ 로 표현해 볼게요.

그러면 다음과 같이 $ix=0,~i2\pi, ~i4\pi$ 가 되면 $e^0 = e^{i2\pi} = e^{i4\pi}=1$ 이 된다는 것을 알 수 있어요.

결국 아래와 같이 한 개의 해는 실수이고, 다른 두개의 해는 복소수가 나오게 되는거에요. (3-6)식을 적용하여 정리하면 다음과 같습니다.

\tag{ex-6} \begin{align} 8^{1/3} = 8^{1/3}(e^{x})^{1/3} &= 2(e^{0})^{1/3}=2 (\cos{0 \over 3} + i\sin{0 \over 3})=2\\ &=2(e^{i2 \pi })^{1/3} = 2\Big(\cos{{2\pi}\over{3}} + i \sin{{2\pi}\over{3}}\Big)=-1+i\sqrt{3}\\ &=2(e^{i4 \pi })^{1/3} = 2\Big(\cos{{4\pi}\over{3}} + i \sin{{4\pi}\over{3}}\Big)=-1-i\sqrt{3} \end{align}

다시 한번 더 말씀드리면 위 식에서 $e^0$ , $e^{i2\pi}$ , $e^{i4\pi}$ 는 (2-3)식의 오일러 공식을 적용해보면 모두 1이 나오는 것을 알 수 있어요. 예를 들어 $e^{i2\pi} = \cos(2\pi)+i\sin (2 \pi) =1$ 이 되는 원리입니다.

또한 $e^{i6\pi}$ , $e^{i8\pi}$ 등도 있을 수 있지만 그 값들을 구해보면 (ex-6)식에서 도출된 세개의 값이 반복될 뿐입니다.

한편, 식에서 나온 $\cos{{2\pi}\over{3}}, \sin {{4\pi}\over{3}}$ 의 값들을 구하는 방법이 궁금하면 여기를 클릭하세요.

4. 복소 삼각함수, 복소 쌍곡선함수, 복소 로그함수

4-1. 복소 삼각함수

$\cos \theta$ , $\sin \theta$ , $\tan \theta$ 가 복소수로 어떻게 표현되는지 알아봐요.

$e^{i\theta}$ 와 $e^{-i\theta}$ 를 서로 합하면 다음과 같아요.

\tag{4-1} \begin{align} e^{i\theta} + e^{-i\theta} = (\cos \theta + i \sin \theta) + (\cos \theta - i \sin \theta) = 2 \cos \theta \end{align}

위 (4-1)식을 $\cos \theta$ 에 대해 정리하면 다음이 성립합니다.

\tag{4-2} \cos \theta = {{e^{i \theta}+e^{-i \theta}}\over{2}}

이번에는 $e^{i\theta}$ 와 $e^{-i\theta}$ 를 서로 빼면 다음과 같아요.

\tag{4-3} \begin{align} e^{i\theta} - e^{-i\theta} = (\cos \theta + i \sin \theta) - (\cos \theta - i \sin \theta) = 2i\sin \theta \end{align}

위 (4-3)식을 $\sin \theta$ 에 대해 정리하면 다음과 같아요.

\tag{4-4} \sin \theta = {{e^{i \theta}-e^{-i \theta}}\over{2i}}

다음에서 $\tan \theta$ 를 구해봐요.

\tag{4-5} \begin{align} \tan \theta &= {{\sin \theta}\over{\cos \theta}}\\[10pt] &={{(e^{i \theta} - e^{-i\theta})/2i}\over{(e^{i\theta}+e^{-i\theta})/2}}\\[10pt] &={{e^{i\theta}-e^{-i\theta}}\over{i(e^{i\theta}+e^{-i\theta})}} \end{align}

위식에서 분자와 분모에 $i$ 를 곱하면 다음과 같이 $\tan \theta$ 를 구할 수 있어요.

\tag{4-6} \tan \theta = -i\Big({{e^{i\theta}-e^{-i\theta}}\over{e^{i\theta}+e^{-i\theta}}}\Big)

4-2. 복소 쌍곡선함수

복소 쌍곡선함수를 다루기 전에 우선 쌍곡선함수를 정리하겠습니다. 그 이유는 복소 쌍곡선 함수를 구하기 위해서는 쌍곡선함수식이 필요하기 때문이에요.

쌍곡사인(hyperbolic sine), 쌍곡코사인(hyperbolic cosine), 쌍곡탄젠트(hyperbolic tangent)는 다음과 같아요.

\tag{4-7} \begin{align} \sinh x = {{e^x - e^{-x}}\over{2}}\\[10pt] \cosh x = {{e^x + e^{-x}}\over{2}}\\[10pt] \tanh x = {{e^x - e^{-x}}\over{e^x + e^{-x}}} \end{align}

그럼 이제부터 복소 쌍곡선함수를 정의하겠습니다.

우선 $\sin ix$ 를 구해봐요. (4-4)식의 $\theta$ 대신에 $ix$ 를 대입하면 됩니다. 그럼 다음이 성립할 거에요.

\tag{4-8} \begin{align} \sin ix &= {{e^{i (ix)}-e^{-i (ix)}}\over{2i}}\\[10pt] &={{e^{-x} - e^{x}}\over{2i}}\\[10pt] &=i{{e^x - e^{-x}}\over{2}}\\[10pt] &=i \sinh x \end{align}

이번에는 $\cos ix$ 를 구해봐요. (4-2)식의 $\theta$ 대신에 $ix$ 를 대입하면 됩니다.

\tag{4-9} \begin{align} \cos ix &= {{e^{i (ix)}+e^{-i (ix)}}\over{2}}\\[10pt] &={{e^{-x} + e^{x}}\over{2}}\\[10pt] &=\cosh x \end{align}

마지막으로 $\tan ix$ 를 구해봐요.

\tag{4-10} \tan ix = {{\sin ix}\over{\cos ix}} = {{i \sinh x}\over{\cosh x}} = i \tanh x

4-3. 복소 로그함수

복소수 $z$ 가 있을 때 다음의 관계가 성립한다고 생각해봐요. 물론 $z \ne 0$ 입니다.

\tag{4-11} z = e^\omega

양변에 자연로그 $\ln$ 을 취한 후 $\omega$ 에 대해 정리하면 다음의 관계가 성립합니다. 이때 복소수 $z$ 는 (2-4)식을 이용하여 $z=re^{i \theta}$ 를 대입합니다.

\tag{4-12} \begin{align} w = \ln z &= \ln (re^{i \theta})\\ &=\ln r + \ln e^{i \theta}\\ &=\ln r + i \theta \end{align}

[예제5] ln(1+i)

$\ln (1+i)$ 를 복소수로 나타내어라.

(sol) (4-12)식을 그대로 적용하면 됩니다. 이때 $(1+i)$ 의 크기는 다음과 같습니다.

\tag{ex-7} \begin{align} r &= \sqrt{x^2+y^2}\\ &=\sqrt{1^2+1^2} \\ &= \sqrt{2} \end{align}

또한 $(1+i)$ 는 실수축으로 1, 허수축으로 1이므로 편각 $\theta$ 는 다음과 같습니다.

\tag{ex-8} \cos \theta = {x \over r} = {1 \over {\sqrt{}2}}

따라서 $\theta = {\pi \over 4}$ 이므로, 최종 답은 다음과 같습니다.

\tag{ex-9} \begin{align} \ln (1+i) &= \ln(\sqrt{2} e^{{i\pi} / 4 })\\ &=\ln{\sqrt{2}} + i{\pi \over 4} \end{align}

[예제6] ln(-1)

$\ln (-1)$ 를 복소수로 나타내어라.

(sol) 실수에서 $\ln(-1)$ 은 값이 존재하지 않아요. 하지만 복소수로 범위를 넓히면 그 값이 존재합니다. 그것을 구해봐요.

우선 다음의 식이 성립함을 우리는 알고 있어요.

\tag{ex-10} -1 = e^{i\pi}

왜냐하면 $e^{i\pi}$ 는 $\cos\pi + i \sin \pi=\cos \pi +0= -1$ 이기 때문이에요.

따라서 정답은 다음과 같습니다.

\tag{ex-11} \begin{align} \ln(-1) &= \ln(e^{i \pi})\\ &=\ln 1 + \ln e^{(i\pi)}\\ &=0+i\pi\\ &=i\pi \end{align}

[예제7] ln(i)

$\ln (i)$ 를 복소수로 나타내어라.

(sol) 이 문제는 위 [예제6]과 동일한 방식으로 풀면 됩니다. 잘 생각해보면 $i$ 는 다음의 관계가 성립함을 알 수 있어요.

\tag{ex-12} i = e^{i\pi/2}

왜냐하면 $e^{i\pi /2}$ 는 $\cos(\pi/2) + i \sin (\pi/2)$ 이기 때문이에요.