여각 공식(cofunction Identity)

BallPen · 2025-10-16T23:15:49+09:00

여각 공식(cofunction identity) 개념과 관련 공식들을 알아 봐요. 어느 각이 주어졌을 때 그 각의 여각이란 90도에서 그 각을 뺀 각도를 뜻해요. sin과 cos, tan과 cot, sec와 csc간에 여각 공식이 성립합니다.

Last Updated on 2025-10-16 by BallPen

삼각함수의 여각공식에 대해 알아 봐요.

어느 각도를 $\theta$ 라할 때 이 각도의 여각(complementary angle)은 $( \pi / 2 - \theta)$ 입니다. 그래서 어느 각과 그 여각을 합하면 아래 (1)식처럼 $\pi \over 2$ rad이 되는 거에요.

\tag{1} \theta + ({\pi \over 2} - \theta) = {\pi \over 2}

그런데 이러한 여각끼리의 관계가 삼각함수에서 항등식으로 나타나는 경우가 있습니다.

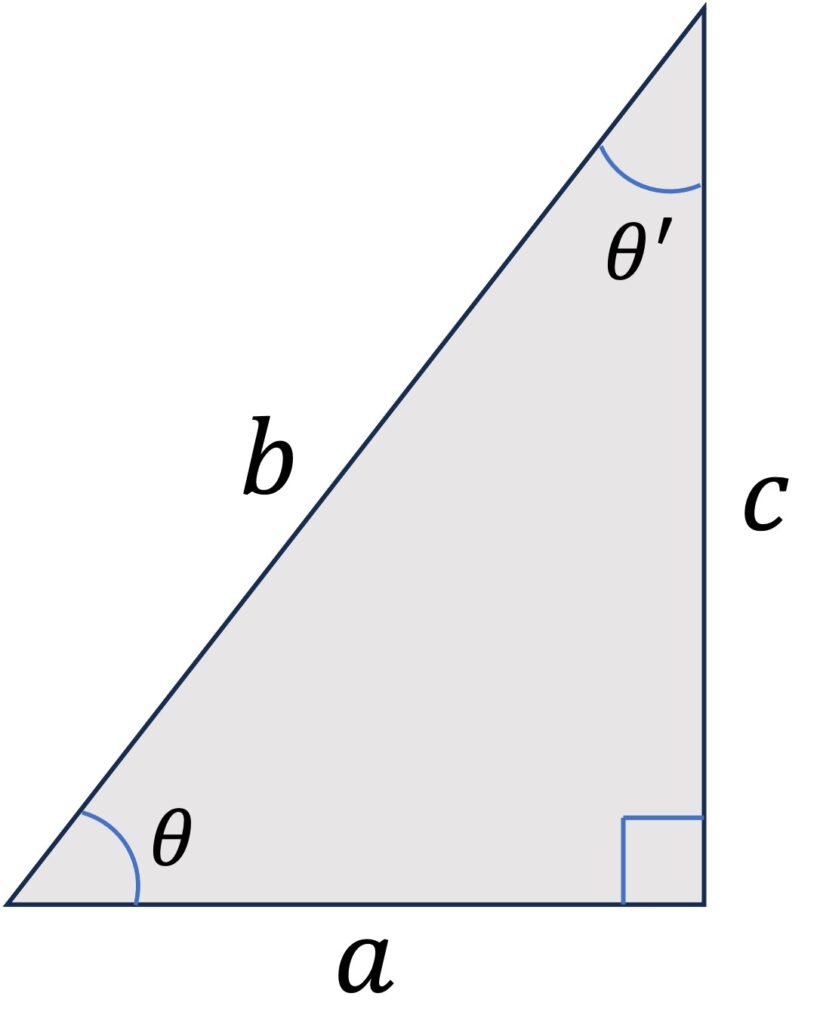
[그림 1]의 직각삼각형이 있을 때 직각을 제외한 한 각도를 $\theta$ 라 하면 나머지 한 각도 $\theta^{\prime}$ 은 $( \pi/2 - \theta)$ 가 되어 여각이 된다는 것을 알 수 있어요.

\tag{2} \begin{align} \pi = \theta+\theta^{\prime} +{\pi \over 2} \end{align}

\tag{3} \begin{align} \theta^{\prime} = {\pi \over 2} - \theta \end{align}

그런데 한 삼각함수에 $\theta$ 를 취했을 때와 다른 삼각함수에 그 여각인 ${\pi \over 2} - \theta$ 를 취했을 때 그 값들이 서로 같아지는 경우가 있어요.

예를 들어, [그림 1]의 직각삼각형을 참고하면 다음 관계가 성립함을 알 수 있어요.

\tag{4} \begin{aligned} &\sin (\theta)= \cos(\theta^{\prime}) = \cos({{\pi}\over{2}}-\theta)\\[10pt] &\cos(\theta) = \sin(\theta^{\prime}) = \sin({{\pi}\over{2}}-\theta)\\[10pt] &\tan (\theta) = \cot(\theta^{\prime})=\cot({{\pi}\over{2}}-\theta) \\[10pt] &\cot (\theta) = \tan(\theta^{\prime})=\tan({{\pi}\over{2}}-\theta) \\[10pt] &\sec (\theta) = \csc(\theta^{\prime})=\csc({{\pi}\over{2}}-\theta) \\[10pt] &\csc (\theta) = \sec(\theta^{\prime})=\sec({{\pi}\over{2}}-\theta) \\ \end{aligned}

이와 같이 sin $\leftrightarrow$ cos, tan $\leftrightarrow$ cot, sec $\leftrightarrow$ csc가 서로 대응하여 서로 여각이 취해질 때 같은 함수 값을 갖게 됩니다.

이 공식을 삼각함수의 여각공식이라고 해요. 참고로 코사인, 코탄젠트, 코시컨트의 ‘코’는 complementary의 co를 뜻해요.

tan 에 대한 여각 공식을 증명해 봐요.

\tag{5} \begin{aligned} \tan({{\pi}\over{2}}-\theta) &= {{\sin({{\pi}\over{2}}-\theta)}\over{\cos({{\pi}\over{2}}-\theta)}}\\[10pt] &={{\sin{\pi \over 2} \cos \theta - \cos{{\pi}\over{2}}\sin\theta}\over{\cos{\pi \over 2}} \cos \theta + \sin{{\pi}\over{2}}\sin \theta}\\[10pt] &={{\cos \theta}\over{\sin \theta}}\\[10pt] &=\cot \theta \end{aligned}

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]