Last Updated on 2025-10-01 by BallPen
피타고라스 삼각 항등식을 증명해 봐요.
피타고라스 삼각 항등식(Pythagorean trigonometric identity)을 증명해 보겠습니다.
아래는 이 글의 목차입니다.
1. 피타고라스 항등식
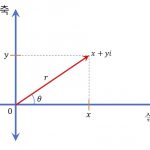
좌표평면위에서 빗변의 길이가 r인 직각삼각형에 피타고라스(Pythagoras) 정리를 적용하면 다음과 같습니다.
\begin{align}
\tag{1}
x^2 + y^2 = r^2
\end{align}그리고 x=r \cos \theta, y=r \sin \theta를 (1)식에 대입하면 다음과 같습니다.
\begin{align}
\tag{2}
(r \cos \theta)^2 + (r \sin \theta)^2 = r^2
\end{align}이 식을 정리하면 다음의 피타고라스 기본 항등식이 유도됩니다.
\begin{align}
\tag{3}
\sin^2 \theta + \cos^2 \theta = 1
\end{align}2. 피타고라스 삼각 항등식
2-1. 첫번째 식
피타고라스 기본 항등식인 (3)식의 양변을 \cos^2 \theta로 나눠 봐요.
\begin{align}
\tag{4}
{{\sin^2 \theta}\over{\cos^2 \theta}} + {{\cos^2 \theta}\over{\cos^2 \theta}} = {1 \over{\cos^2 \theta}}
\end{align}그러면 다음 식이 성립합니다.
\begin{align}
\tag{5}
\tan^2 \theta + 1 = \sec^2 \theta
\end{align}2-2. 두번째 식
이번에는 피타고라스 기본 항등식인 (3)식의 양변을 \sin^2 \theta로 나눠 봐요.
\begin{align}
\tag{6}
{{\sin^2 \theta}\over{\sin^2 \theta}} + {{\cos^2 \theta}\over{\sin^2 \theta}} = {1 \over \sin^2 \theta}
\end{align}그러면 다음 식이 성립합니다.
\begin{align}
\tag{7}
1 + \cot^2 \theta = \csc^2 \theta
\end{align}흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 2 Average: 5]
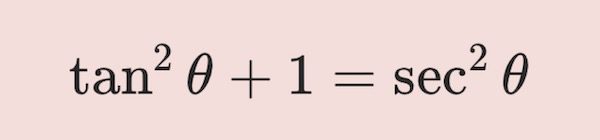


2022년 고3때 대학 면접 준비하면서 글 자주 보다가 정말 오랜만에 들어와봤는데 아직도 활동하시는걸 보니 괜히 찡하네요 ㅎㅎ 활동 자주하셔서 너무 좋습니다!
아이고 감사합니다. 인공지능 때문에 블로그 방문객이 많이 줄었지만 저는 나름대로 계속 하려고 합니다. 자주 방문해 주세요. 고맙습니다. ㅎㅎ