Last Updated on 2025-09-30 by BallPen
함수의 대칭성을 표현하는 우함수(짝함수)와 기함수(홀함수)에 대해 명확히 구분해 봐요.
우함수와 기함수 개념은 함수의 대칭성을 기준으로 구분합니다.
이에 대해 자세히 알아 봐요.
1. 우함수(Even Function, 짝함수)
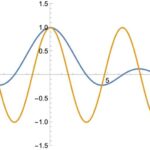
우함수는 그래프가 y축에 대해 대칭인 함수예요. 쉽게 말해 y축을 중심으로 데칼코마니처럼 접으면 완전히 겹쳐지는 모양이죠.
- 수학적 정의 : 함수 f(x)에 대해 x 대신 −x를 넣어도 함수값이 똑 같아요.
\begin{align}
f(-x) = f(x)
\end{align}- 그래프 특징 : y축 대칭입니다.
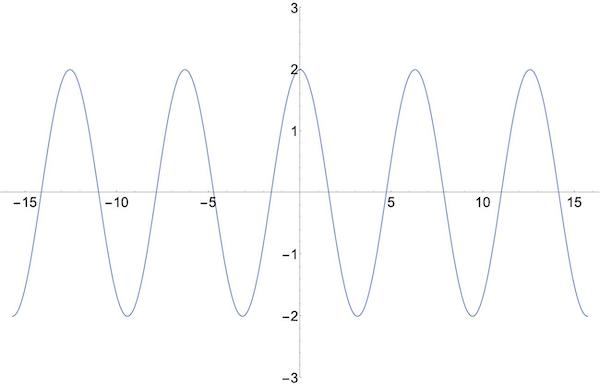
- 예) 코사인(cosine)함수
\begin{align}
\tag{2}
\cos(-x) = \cos(x)
\end{align}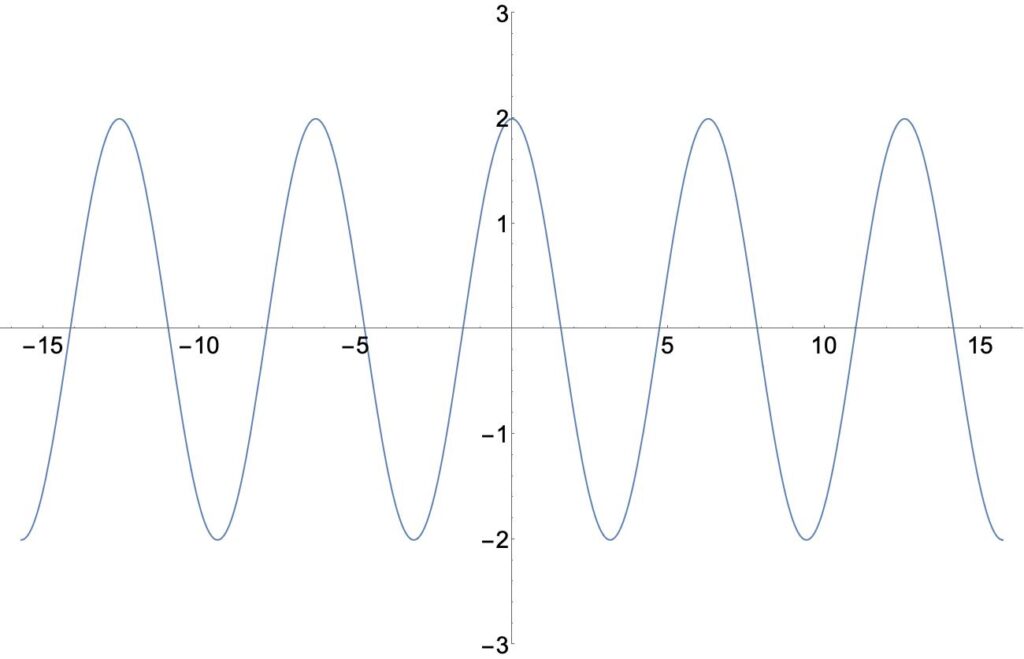
2. 기함수(Odd Function, 홀함수)
기함수는 그래프가 원점에 대해 대칭인 함수예요. 함수 위의 한 점을 원점을 기준으로 180도 회전시키면 그래프 위의 다른 점과 만나게 되는 함수를 말해요.
- 수학적 정의 : 함수 f(x)에 대해 x 대신 −x를 넣으면 원래 함수값에 마이너스(-)가 붙은 결과가 나와요.
\begin{align}
\tag{3}
f(-x) = - f(x)
\end{align}- 그래프 특징 : 원점 대칭입니다.
- 예1) 사인(sine)함수
\begin{align}
\tag{4}
\sin(-x) = - \sin (x)
\end{align}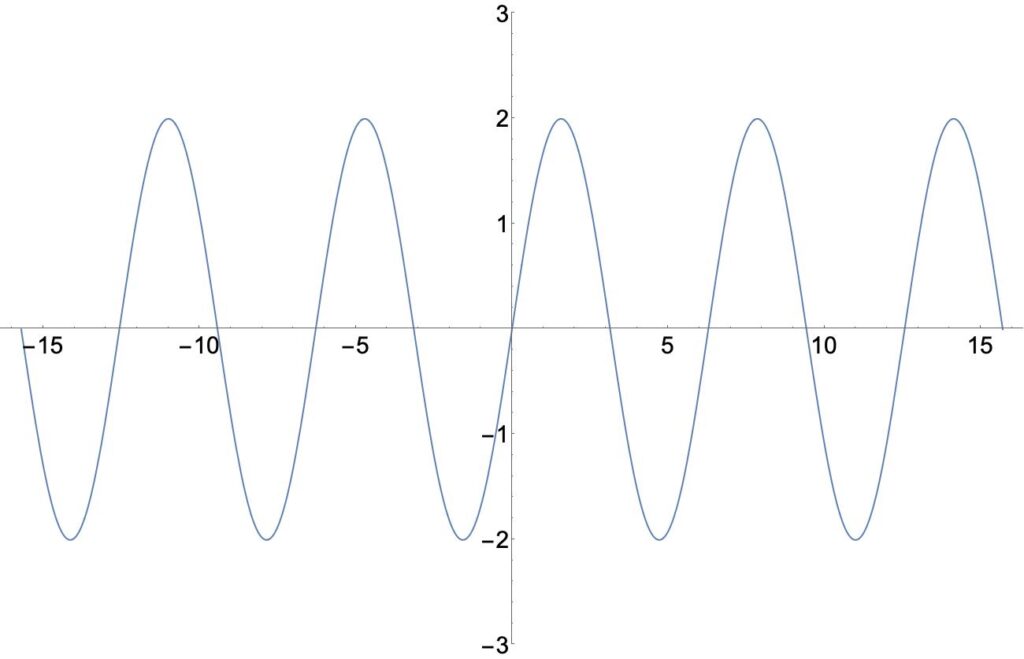
- 예2) 탄젠트(tangent)함수
\begin{align}
\tag{5}
\tan(-x) = - \tan (x)
\end{align}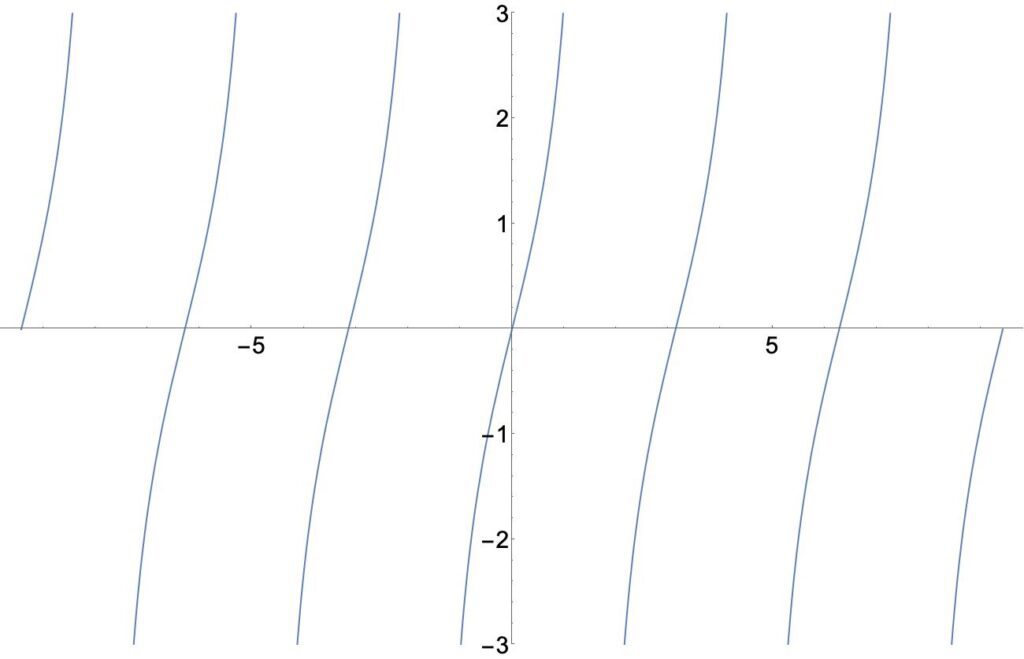
3. 요약
우함수(짝함수)는 그래프가 y축에 대해 대칭이며, 수학적으로는 f(-x) = f(x)의 조건을 만족하는 함수로 정의되며 코사인 함수가 대표적인 예시입니다.
반면에 기함수(홀함수)는 그래프가 원점에 대해 대칭이며, 수학적 정의는 f(-x) = -f(x)의 조건을 만족하는 함수이고 사인 및 탄젠트 함수가 예시입니다.
흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 1 Average: 5]


“우함수와 기함수”에 대한 1개의 생각