BallPen.blog, 내 나이의 빛깔
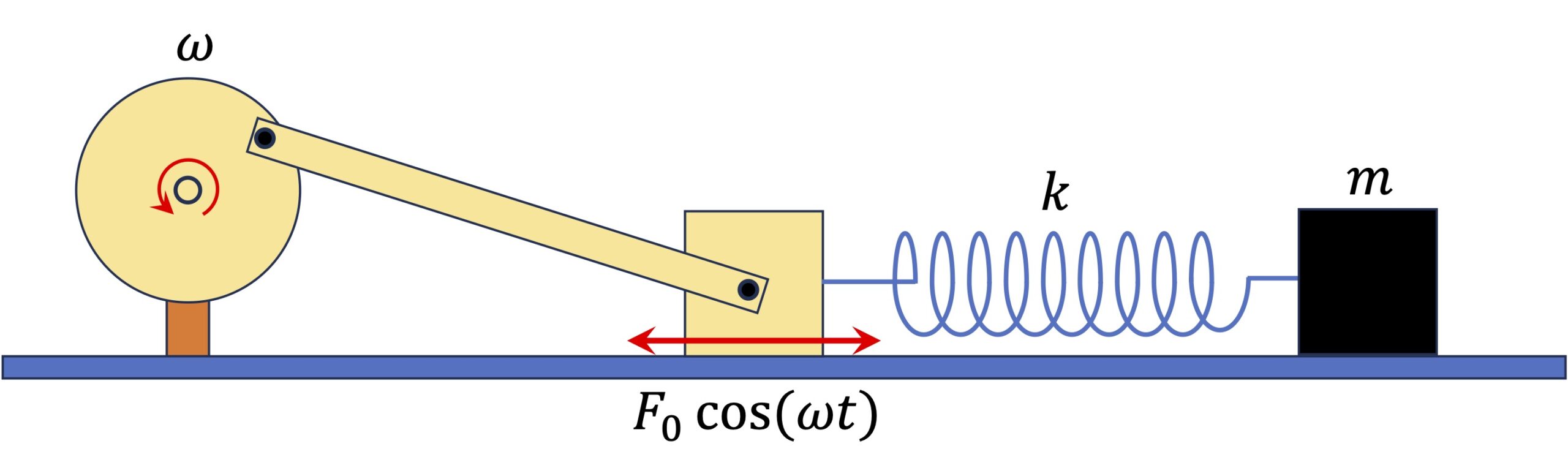
역제곱 중심력이 작용할 때 행성 궤도가 갖는 에너지를 구해 봐요. 행성 궤도의 에너지 크기는 행성이 타원궤도를 갖는지 아니면 포물선궤도나 쌍곡선궤도를 갖는지에 따라 달라집니다. 그리고 행성 궤도를 알기 위해서는 이심율 을 구해야 하는데요. 이심율은 행성의 궤도 방정식으로도 구할 수 있지만 이 글에서 소개하는 궤도의 에너지 방정식을 통해 구할 수도 있어요. 궤도의 에너지 방정식은 다음과 같아요. 여기서 … Read more
입자의 궤도방정식에 역제곱 중심력을 대입하면 타원궤도가 얻어짐을 알아 봐요. 케플러 제1법칙(Kepler’s 1st law of planetary motion)이란 태양을 한 초점으로 하는 타워궤도를 따라 행성이 공전한다는 법칙입니다. 따라서 이 법칙을 타원궤도의 법칙이라고도 불러요. 이 법칙은 입자의 궤도방정식에 역제곱 중심력을 대입하여 공전각도 \(\theta\)에 따른 입자의 궤도식을 구함으로써 명확이 입증할 수 있습니다. 그 결과는 다음 식으로 주어져요. \begin{align}\tag{D1}r = … Read more
중심력장 하에서 움직이는 입자의 궤도를 구하는 미분방정식을 알아 봐요. 입자의 궤도 방정식(differential equation of the orbit of a particle)이란 어떤 중심력(Central Force) 하에서 움직이는 입자가 무슨 궤도를 갖게 되는지를 구할 수 있는 미분방정식입니다. 이 방정식에 중심력을 대입하여 풀면 \(\theta\)의 함수로 원점으로부터 입자까지의 거리 \(r\)을 구할 수 있어요. 그래서 \(\theta\)의 범위에 따라 \(r\)의 값을 구한 후 … Read more
패러데이 법칙과 유도전기장에 대해 알아 봐요. 패러데이 법칙(Faraday’s law)이란 패러데이(Michael Faraday)가 발견한 전자기유도법칙으로 시간에 따라 변하는 자기장선속(magnetic flux)이 기전력을 생성한다는 법칙입니다. 이 법칙의 일반형은 다음과 같아요. \begin{align}\oint_c \vec E \cdot d \vec l = – {{d \Phi_B}\over{dt}}\end{align} 위 식에서 적분기호 밑의 \(c\)는 closed의 머리글자로 닫힌 경로를 뜻합니다. \(\Phi_B\)는 자기장 선속을 의미하고 이 자기장 선속이 시간에 … Read more
한번 흔들어진 진동자가 얼마나 오랫동안 진동을 유지할 수 있는가의 척도인 Q 인자에 대해 알아 봐요. Q 인자(quality factor)는 Q 인수, Q 값이라고도 불리는데요. 이 인자는 진동을 시작한 진동자가 얼마나 오랬동안 그 진동을 유지할 수 있는가의 척도입니다. 예를 들어, 공기 중 용수철에 매달린 물체를 당겼다가 놓으면 진동을 시작하는데요. 당연히 오랫동안 그대로 두면 공기저항력에 의해 진동이 멈추게 … Read more
감쇠가 있는 강제진동자의 진동 특성을 알아 봐요. 강제진동자(driven oscillator)란 외부 강제력이 작용하는 조화진동자를 뜻합니다. 일반적으로는 감쇠가 있는 강제진동자라고 불러요. 왜냐면 감쇠가 없는 경우는 이상적으로만 존재할 뿐이니까요. 감쇠가 있는 강제진동자의 진동 변위 \(x(t)\)는 다음 식으로 표현됩니다. \begin{align*}x(t) = {{F_0 /m}\over{\sqrt{(\omega_0^2 – \omega^2)^2 + (2 \gamma \omega)^2}}} \exp \big( {i (\omega t – \tan^{-1} {{2 \gamma \omega}\over{\omega_0^2 … Read more
진동 및 파동함수를 복소지수함수로 표현하는 방법과 그 이유를 알아 봐요. 진동 및 파동함수의 복소지수함수 표기 방법과 그렇게 표기하는 이유를 알아 봐요. 아래는 이번 글의 목차입니다. Contents1. 진동 및 파동함수의 복소지수함수 표기 방법1-1. 진동함수의 복소지수함수 표기1-2. 파동함수의 복소지수함수 표기2. 진동 및 파동함수를 복소지수함수로 표기하는 이유 1. 진동 및 파동함수의 복소지수함수 표기 방법 1-1. 진동함수의 복소지수함수 표기 … Read more
군속도와 위상속도의 개념을 알아 봐요. 군속도 개념에 대한 이야기입니다. 파동의 속도에는 위상속도(phase velocity, 위상속력)와 군속도(group velocity, 군속력)가 있어요. 위상 속도는 알겠는데 군속도가 무엇인지 어려워 하는 경우가 있어요. 또 그 둘의 차이점을 명확히 설명하지 못하는 경우가 많아요. 결론부터 말씀드리면 위상속도 \(v_p\)는 다음 식으로 주어집니다. \begin{align}\tag{D1}v_p = {\omega \over k}\end{align} 여기서 \(\omega\)는 파동의 각진동수, \(k\)는 파동의 파수(wave … Read more
파동이 한 주기 동안 전달하는 에너지, 즉 평균 일률이 무엇에 의존하는지 알아봐요. 파동에너지, 즉 파동이 전달하는 에너지 식이 어떻게 표현되는지 유도해보고 그 의미를 알아보도록 해요. 결론부터 말씀드리면 조화진동하는 파동이 한주기 동안 전달하는 평균 파동에너지(또는 평균 일률) \(<E>\)는 다음 식으로 주어집니다. 평균을 취하는 이유는 한 주기 동안 파동에너지가 계속 변하기 때문이에요. \begin{align}\tag{D1}<E> ={1 \over 2} m\omega_0^2 … Read more
가둬진 물에 의해 댐이 받는 정압력과 정수력을 계산해 보도록 해요. 정압력 계산 방법을 알아 보겠습니다. 여기서 정압력(hydrostatic pressure, 또는 정수압)이란 가둬진 물에 의해 댐이 받는 압력(pressure)을 뜻합니다. 물이 흐를 때의 압력인 동압력(hydrodynamic pressure, 동수압)과는 달리 정지한 물에 의한 압력임을 의미해요. 아울러 이 정압력 때문에 댐이 받게 되는 힘인 정수력(hydrostatic force)도 계산해 보도록 해요. 간단한 문제이니 … Read more