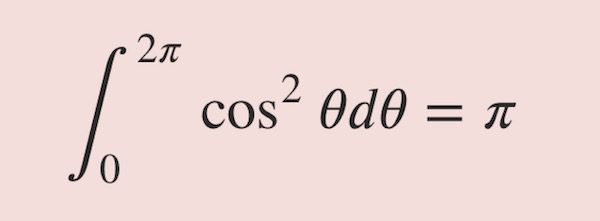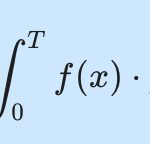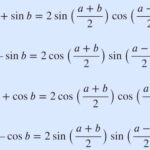Last Updated on 2025-08-05 by BallPen
한 주기에 걸친 코사인 제곱 함수의 적분을 계산해 봐요.
코사인 제곱 함수 적분 방법을 알아 봐요. 즉, 다음의 적분을 계산해 보자는 거에요.
\begin{align}
\tag{1}
\int_0^{2\pi} \cos^2 \theta d \theta
\end{align}
이 계산을 위해서는 코사인 두배각 공식을 적용하는게 좋아요. 그 공식은 다음과 같아요.
\begin{align}
\tag{2}
\cos 2 \theta = 2 \cos^2 \theta -1
\end{align}
위 (2)식을 \(\cos^2 \theta\)에 대해 풀면 다음과 같아요.
\begin{align}
\tag{3}
\cos^2 \theta = {1 \over 2} \Big(\cos 2 \theta + 1 \Big)
\end{align}
이제 (3)식을 (1)식에 대입하고 적분합니다. 적분방법은 다음과 같아요.
\begin{align}
\tag{4}
\require{cancel}
\int_0^{2\pi} \cos^2 \theta d \theta &= {1 \over 2} \int_0^{2 \pi} (\cos 2 \theta + 1) d \theta\\
&={1 \over 2} \Big[ {1 \over 2} \sin 2 \theta +\theta \Big]_0^{2\pi}\\
&={1 \over 2} \Big[{1 \over 2} \sin 4\pi +2 \pi – 0+0\Big]\\
&={1 \over {\cancel 2}} {\cancel 2}\pi\\
&=\pi
\end{align}
결국 코사인 제곱 함수 적분 결과는 다음과 같습니다.
\begin{align}
\tag{5}
\int_0^{2 \pi} \cos^2 \theta d \theta = \pi
\end{align}