Last Updated on 2025-09-01 by BallPen
열역학적 과정 중 등압 과정에 대한 이야기입니다.
등압 과정 (isobaric process)은 대표적인 열역학적 과정 중의 하나입니다. 열역학을 공부할 때 등적 과정, 단열 과정, 등온 과정과 함께 항상 등장하는 과정이에요.
지난 글인 단열 과정에 이어 기체 분자의 운동을 상상하면서 등압 과정도 함께 이해해 봐요.
아 참 등압 과정은 정압 과정이라고도 불립니다.
시작하겠습니다. 아래는 이번 글의 목차입니다.
Contents
1. 주요 개념 복습
아래 내용은 등압 과정을 이해하기 위해 알아야 할 열역학의 주요 개념들입니다.
한번 쭉 읽어보시되 세부적인 내용이 잘 이해가지 않더라도 일단 이러한 관계가 성립하는구나 하고 편하게 접근하시기 바랍니다.
첫째, 열량 Q는 뜨거운 물체에서 차가운 물체로 전달되는 에너지입니다.
둘째, 내부에너지 U의 크기는 계 내에 있는 기체 분자의 온도 T에 비례합니다. 여기서 기체 분자의 온도란 기체 분자의 운동에너지 KE와 관련된 양입니다. 결국 기체분자의 움직임이 빠르면 KE가 크고, 온도 T가 높으며, 내부에너지 U도 큰 것으로 보세요.
\tag{1}
\color{blue}U \propto T \propto KE따라서 내부에너지 변화량 \Delta U는 다음과 같이 주어집니다.
\tag{2}
\color{blue}\Delta U \propto \Delta T \propto \Delta KE셋째, 계의 기체 분자가 한 일 W는 계의 부피 변화량 \Delta V에 비례합니다. 계의 압력 P가 일정한 상태에서 계의 부피가 \Delta V만큼 변했다면 일 W는 다음과 같습니다.
\tag{3}
\color{blue}W= P \Delta V만일 부피가 변하는 동안 압력 P가 달라진다면 (3)식은 다음과 같이 적분의 형태로 표현할 수 있어요.
\tag{4}
\color{blue}W= \int P \mathrm {d}V넷째, 마지막으로 계 내부의 압력 P는 기체 분자의 운동에너지 KE를 계의 부피 V로 나눈 값으로 정의됩니다.
\tag{5}
\color{blue}P \propto {T \over V} \propto {{KE}\over{V}}2. 등압 과정
등압 과정은 외부의 열원으로부터 열량 Q를 전달 받은 계가 외부로 일 W를 하는 과정에서 계 내부의 압력이 일정하게 유지되는 열역학적 과정을 말합니다.
압력이 일정하게 유지되는 과정이라고 하여 등압 과정이라 부릅니다.
등압 과정이 일어나는 동안의 기체 분자 운동, 열역학 제1법칙, PV 도표가 어떻게 달라지는지 순서대로 알아보겠습니다.
아래 [그림 1]에 실린더가 하나 있어요. 이 실린더의 측면 벽은 외부와 열적으로 단열되어 열의 유입이나 유출이 없으나, 실린더의 아래쪽은 고온의 열원과 접촉되어 있어요.
또한 실린더 위쪽에 있는 피스톤은 실린더 내의 기체 분자가 충돌하게 됨으로써 밀려 올라갈 수 있어요.
이번 글에서는 등압 과정에서 계가 외부로 일을 하는 경우만 다르겠습니다.
![[그림 1] 등압 과정. 실린더 내에 온도 <span class="katex-eq" data-katex-display="false">T_1</span>의 기체 분자가 들어 있으며, 이 실린더는 온도 <span class="katex-eq" data-katex-display="false">T_h</span>인 고온의 열원과 열적으로 접촉되어 있어요. 실린더 내의 압력 <span class="katex-eq" data-katex-display="false">P</span>가 일정하게 유지되는 상태에서 외부로 일 <span class="katex-eq" data-katex-display="false">W</span>를 하게 되면 등압과정이라 부릅니다.](https://ballpen.blog/wp-content/uploads/2022/07/Picture1-3-1024x667.jpg)
2-1. 등압 과정에서의 분자 운동
[그림 1]에는 기체 분자 4개가 그려져 있어요. 그중 \textcircled{1}번의 기체 분자는 T_1의 온도와 그에 대응하는 운동에너지 KE_1을 갖고 있어요.
이때 그림에 있는 화살표 길이를 운동에너지의 크기로 보아주시기 바랍니다.
이 기체 분자는 T_h인 고온의 열원과 충돌하면서 열원으로부터 열량 Q를 흡수하게 됩니다. 열량은 높은 온도에서 낮은 온도로 전달되는 에너지라는 것을 꼭 기억하세요.
열원과 충돌한 후의 기체 분자를 표현한 것이 \textcircled{2}번 분자에요.
열원과의 충돌에 의해 \textcircled{2}번 분자는 \textcircled{1}번 분자의 진행방향과 반대가 되었어요.
또한 화살표 길이인 운동에너지 크기가 열원과 충돌하는 과정에서 전달된 에너지 Q만큼 더 커진 것을 볼 수 있습니다.
이것은 열원과의 충돌에 의해 기체분자의 운동에너지와 온도가 상승하였음을 뜻해요. 이때 온도를 T_2로, 그에 상응하는 운동에너지를 KE_2로 표기할게요.
\textcircled{2}번 분자는 계속 이동하여 그림의 \textcircled{3}번 분자처럼 실린더의 피스톤과 충돌합니다.
그런데 이 피스톤은 실린더의 다른 벽들과는 다르게 기체 분자와의 충돌에 의해 밀려 올라갈 수 있어요. 물론 수많은 기체 분자들이 피스톤과 충돌하는 것을 상상하셔야 합니다.
이에 따라 \textcircled{3}번 분자가 피스톤과 충돌함으로써 피스톤이 최초 위치 A에서 나중 위치 B로 움직이게 됩니다.
결국 기체가 들어있는 원통형 실린더의 내부 부피가 증가하게 되어 팽창하게 되는 것이죠.
그렇다면 충돌한 후의 기체 분자는 어떻게 될까요? 바로 \textcircled{4}번 분자와 같습니다.
\textcircled{3}번 분자와 비교하여 운동방향이 반대로 바뀌었고요. 그 다음에는 화살표의 길이에 대응하는 운동에너지의 크기가 작아진 것을 알 수 있습니다.
이것은 \textcircled{3}번 기체의 온도 T_2에 비해 \textcircled{4}번 기체의 온도 T_3가 더 낮아진 것을 뜻해요.
이때 중요한 것은 \textcircled{4}번 기체의 온도 T_3는 바로 위에서 말씀드렸듯이 T_2보다는 작지만 최초의 온도 T_1보다는 높아요.
이러한 관계는 [그림 1]의 화살표 길이를 잘 보시면 이해하실 수 있어요.
이러한 과정이 계속 반복됩니다. 즉 [그림 1]의 \textcircled{4}번 분자는 \textcircled{1}번 분자가 되어 순환하게 되는 것이죠.
결국, 실린더 내의 기체 분자는 순환을 거듭하면서 온도가 계속 상승하여 기체 분자의 운동에너지가 계속 증가합니다. 아울러 기체분자는 피스톤과 계속 충돌하여 실린더 내부 공간을 팽창시키죠.
이때 (5)식에서 설명드렸던 것처럼, 실린더 내의 부피 V와 기체분자의 온도 T사이의 비율값이 일정하게 유지되면 압력 P가 일정한 등압 과정이 이루어지게 되는 것이죠.
2-2. 등압 과정에서의 열역학 제1법칙
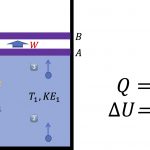
등압 과정에서 열역학 제1법칙은 에너지보존법칙으로서 \Delta U = Q - W가 성립합니다.
계는 고온의 열원으로부터 열량 Q를 전달받고, 그 에너지중 일부를 계의 부피를 팽창시키는 일 W를 하는데 소모합니다. 나머지 남은 에너지는 계의 내부에너지를 \Delta U만큼 변화시키죠.
2-3. 등압 과정에서의 PV 도표
PV 도표(또는 PV 다이어그램)를 이용하면 계의 압력, 부피, 온도의 상태변수를 하나의 점으로 표현할 수 있어요.
아래 [그림 2]는 등압 과정 동안 PV 도표가 어떻게 변하는지를 보여주고 있습니다.
![[그림 2] 등압 과정에 대한 PV 도표. <span class="katex-eq" data-katex-display="false">A</span>점이 <span class="katex-eq" data-katex-display="false">B</span>점으로 이동하는 것이 등압 과정입니다. 이때 <span class="katex-eq" data-katex-display="false">T_1 < T_2</span>입니다.](https://ballpen.blog/wp-content/uploads/2022/07/Picture5-1024x843.jpg)
[그림 2]와 같이 등압 과정은 일정한 압력 P하에서 A점이 B점으로 달라지는 열역학적 과정입니다.
이 과정에서 계 내부의 온도는 T_1에서 T_2로 상승하게 되고요. 부피는 처음 V_A에서 나중 V_B로 증가합니다.
이때 압력이 P로 일정하게 유지되기 위해서는 (5)식과 같이 부피 증가와 온도 증가의 비율이 항상 같아야만 합니다.
3. 등압 과정에서 한 일의 크기
[그림 2]에서와 같이 등압 과정이 일어나는 동안 계의 부피는 증가하게 됩니다. 그러므로 계가 주변으로 일 W를 하게 되는데요.
그 일의 크기를 구해보겠습니다.
압력 P인 계 내의 기체분자는 피스톤과 충돌하면서 피스톤에 힘 F를 가하게 됩니다. 이때 피스톤의 면적을 A라고 했을 때 기체에 의해 피스톤에 가해지는 힘은 다음과 같습니다.
\tag{6}
F=PA이 힘 F에 의해 피스톤이 \Delta d만큼 밀려올라갔다면 기체가 한 일 W은 다음과 같습니다.
\tag{7}
W=F\Delta d = PA\Delta d = P \Delta V(7)식에서 A\Delta d는 부피의 변화량 \Delta V와 같습니다.
결국 (7)식에 따르면 압력이 일정한 경우 계가 한 일 W는 압력 P와 부피 변화량 \Delta V의 곱과 같습니다.
그리고 이것은 PV 도표에서 A에서 B로 향하는 경로의 아래 면적에 해당합니다.
\tag{8}
W = P \Delta V = P(V_B - V_A)지금까지 등압 과정에 대해 말씀드렸습니다.
4. 등압 과정 예제
1기압의 기체가 들어있는 어느 실린더가 있다. 이 실린더 안에는 넓이가 0.20 \mathrm{m^2}인 피스톤이 있다. 압력을 일정하게 유지하면서 2.52 \times 10^4 \mathrm{J}의 열량을 가하였더니 피스톤이 0.50 \mathrm{m}만큼 밀려났다.
(a) 이 과정에서 기체가 외부에 한 일의 크기는 얼마인가?
(풀이)
(7)식을 적용하여 한 일의 크기 W를 구합니다.
\tag{Q-1}
\begin{aligned}
W&=P \Delta V = PA\Delta d \\[8pt]
&= 1.013 \times 10^5 ~\mathrm{ N/m^2} \times 0.20~\mathrm{m^2} \times 0.50~\mathrm m\\[8pt]
&=1.01 \times 10^4 ~\mathrm{J}
\end{aligned}(b) 기체의 내부에너지는 얼마나 증가하는가?
(풀이)
위에서 설명드렸던 열역학 제1법칙을 적용하면 됩니다.
\tag{Q-2}
\begin{aligned}
\Delta U &= Q - W\\[8pt]
&=2.52 \times 10^4 \mathrm{J} - 1.01 \times 10^4 \mathrm{J}\\[8pt]
&=1.51 \times 10^4 \mathrm{J}
\end{aligned}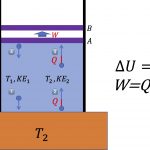


3번 분자와 비교하여 운동방향이 반대로 바뀌었고요. 그 다음에는 화살표의 길이에 대응하는 운동에너지의 크기가 작아진 것을 알 수 있습니다.
이렇게 말씀해주셨는데 질문이 두가지 생겼습니다 ..!
1. 가정상 기체 분자들은 탄성 충돌을 하는데 운동에너지의 크기가 어떻게 작아질 수 있는건가요 ??
2. 기체 분자가 열을 흡수하는 방식이 열원에 충돌하는 것이라면, 열에너지를 빼낼 때는 어떤 방식을 사용하나요 ?? (등압 압축같은 경우 ..)