Last Updated on 2024-01-06 by BallPen
미분방정식이란 무엇일까요? 함께 알아보겠습니다.
미분방정식(differential equation)이란 순간변화율로 표현되어 있는 방정식을 말합니다. 즉 방정식에 미분이 포함되어 있는 거에요.
이러한 미분방정식은 물리학을 포함한 수많은 분야에서 자주 나타납니다.
아직은 미분방정식이 무엇인지 많이 생소할텐데요. 일단 이번 글에서는 그 미분방정식이란 무엇이고 그 특징들을 설명드리겠습니다.
아래는 이번 글의 목차입니다.
Contents
1. 미분
독립변수 x가 연속적으로 변함에 따라 종속변수 y도 연속적으로 변할 때, 어느 한 점에서 종속변수 변화량 \Delta x와 독립변수 변화량 \Delta y의 비율의 극한을 그 점에서의 ‘미분계수’ 또는 ‘순간변화율’이라고 합니다.
이에 비해 단순히 종속변수 변화량 \Delta x와 독립변수 변화량 \Delta y의 비율을 평균변화율이라 하죠.
1-1. 평균변화율
x가 a로부터 a+\Delta x인 b로 변화될 때 함수 f(x)의 평균 변화율은 다음과 같습니다.
\tag{1}
\begin{align}
{{\Delta y}\over{\Delta x}} &= {{f(a+\Delta x)-f(a)}\over{\Delta x}}\\
&={{f(b)-f(a)}\over{b-a}}
\end{align}아래 [그림 1]에서 파랑색 직선의 기울기가 평균변화율을 뜻합니다.
![[그림 1] 빨강색 선은 함수 <span class="katex-eq" data-katex-display="false">y=f(x)</span>의 곡선을 나타냅니다. 그리고 파랑색 선의 기울기가 평균변화율을 주황색 선의 기울기가 <span class="katex-eq" data-katex-display="false">a</span>인 지점에서의 순간변화율을 나타냅니다. 즉 <span class="katex-eq" data-katex-display="false">\Delta x</span>가 0으로 가는 평균변화율의 극한이 순간변화율입니다.](https://ballpen.blog/wp-content/uploads/2022/10/Picture1.jpg)
1-2. 순간변화율 (미분계수)
(1)식에서 \Delta x \rightarrow 0일 때의 극한값이 순간변화율입니다. 수학적으로 표현하면 아래 식과 같습니다.
\tag{2}
\begin{align}
\lim_{\Delta x \rightarrow0} {{\Delta y}\over{\Delta x}} &= \lim_{\Delta x \rightarrow 0}{{f(a+\Delta x)-f(a)}\over{\Delta x}}\\
&=\lim_{b \rightarrow a} {{f(b)-f(a)}\over{b-a}}
\end{align}이때 (2)식은 너무 길어 평소에 사용하기 불편하잖아요. 이를 줄여서 다음과 같이 표현합니다. 읽을때는 x=a지점에서의 순간변화율 (또는 미분계수, 또는 기울기)이라고 합니다.
무엇을 사용하든 다 똑같은 의미에요.
\tag{3}
f ^\prime (a), ~~y^\prime _{x=a} , ~~{{dy}\over{dx}}\Big|_{x=a}[그림 1]에서 주황색 직선의 기울기가 a인 지점에서의 순간변화율을 뜻합니다.
[예제1] 순간변화율
f(x) = \sqrt{x}인 함수가 있다. x=1에서의 미분계수를 구하여라.
[풀이] 아래와 같이 미분계수는 1/2이 나옵니다. 한편 풀이에서 빨강색 부분은 같은 양을 나누고 곱해주었음을 뜻합니다.
\tag{E-1}
\begin{align}
f^{\prime}(1) &=\lim_{\Delta x \rightarrow0} {{f(1+\Delta x) -f(1)}\over{\Delta x}} \\
&=\lim_{\Delta x \rightarrow0} {{\sqrt{1+\Delta x} -\sqrt{1}}\over{\Delta x}} \\
&=\lim_{\Delta x \rightarrow0} {({\sqrt{1+\Delta x} -\sqrt{1})\color{red}({\sqrt{1+\Delta x} +\sqrt{1})}}\over{\Delta x}\color{red}({\sqrt{1+\Delta x} +\sqrt{1})}} \\
&=\lim_{\Delta x \rightarrow{0}} {{(1+\Delta x)-1}\over{{\Delta x}}\color{black}({\sqrt{1+\Delta x} +\sqrt{1})}}\\
&=\lim_{\Delta x \rightarrow 0}{{\cancel{\Delta x}}\over{\cancel{\Delta x}(\sqrt{1+\Delta x}+\sqrt{1})}}\\
&=\lim_{\Delta x \rightarrow 0}{{1}\over{\sqrt{1+\Delta x}+\sqrt{1}}}\\
&={1 \over 2}
\end{align}이 결과가 뜻하는 것은 x=1에서 f(x) = \sqrt{x}의 순간기울기가 1/2임을 나타냅니다.
1-3. 도함수와 미분
(2)식에 주어진 특정 지점 a대신 독립변수 x를 대입하면 어느 지점에서든 미분계수를 구할 수 있는 함수를 도출할 수 있습니다. 이때 이 함수를 x에 관한 y의 도함수라고 합니다.
그리고 이 도함수를 구하는 과정을 “함수 f(x)를 x에 관해 미분한다”라고 말합니다.
미분을 기호로 표현하면 다음과 같습니다. 무엇을 사용하든 같은 의미입니다.
\tag{4}
y^{\prime},~~f ^\prime (x), ~~{{dy}\over{dx}},~~{{df(x)}\over{dx}}[예제2] 도함수
f(x) = \sqrt{x}인 함수가 있다. 이 함수의 도함수를 구하여라
[풀이] 도함수는 아래와 같이 구해집니다.
\tag{E-2}
\begin{align}
f^{\prime}(x) &=\lim_{\Delta x \rightarrow0} {{f(x+\Delta x) -f(x)}\over{\Delta x}} \\
&=\lim_{\Delta x \rightarrow0} {{\sqrt{x+\Delta x} -\sqrt{x}}\over{\Delta x}} \\
&=\lim_{\Delta x \rightarrow0} {({\sqrt{x+\Delta x} -\sqrt{x})\color{red}({\sqrt{x+\Delta x} +\sqrt{x})}}\over{\Delta x}\color{red}({\sqrt{x+\Delta x} +\sqrt{x})}} \\
&=\lim_{\Delta x \rightarrow{0}} {{(x+\Delta x)-x}\over{{\Delta x}}\color{black}({\sqrt{x+\Delta x} +\sqrt{x})}}\\
&=\lim_{\Delta x \rightarrow 0}{{\cancel{\Delta x}}\over{\cancel{\Delta x}(\sqrt{x+\Delta x}+\sqrt{x})}}\\
&=\lim_{\Delta x \rightarrow 0}{{1}\over{\sqrt{x+\Delta x}+\sqrt{x}}}\\
&=\lim_{\Delta x \rightarrow 0}{1\over{\sqrt{x}+\sqrt{x}}}\\
&={1 \over 2}x^{-{{1}\over{2}}}
\end{align}한편, x=1에서의 미분계수를 구한고자 한다면 위의 도함수에서 x대신에 1을 대입하면 됩니다. 그러면 (E-1)식과 같이 1/2이 동일하게 구해지는 것을 알 수 있습니다.
결국 도함수를 구해 놓으면 어느 지점에서건 미분계수를 쉽게 구할 수 있게 됩니다. 다양한 함수의 미분법은 여기를 참고하세요.
1-4. 상미분
위에서 도함수를 구하는 과정을 미분이라고 했는데요. 이때 원래 함수의 독립변수가 하나인 경우 이 함수를 미분하는 것을 상미분이라고 합니다.
통상적인 미분이라는 뜻이에요.
상미분 개념은 예를 들어 어떤 기계장치의 온도가 기계로 들어가는 교류신호의 실효값에만 의존하는 경우 실효전압의 크기가 증가함에 따라 온도가 어떠한 기울기로 증가하는 지를 알고자 할 때 적용할 수 있습니다.
구체적인 예로는 위 [예제2]가 바로 상미분에 해당합니다. 예제에서 x를 교류 실효값의 크기라 생각하고 f(x)를 온도라고 생각하면 됩니다.
1-5. 편미분
상미분은 변수가 하나인 경우의 미분이라면 편미분은 변수가 2개 이상인 경우의 미분법을 말합니다.
편미분은 하나의 변수에 대해 미분할 때 다른 변수는 상수로 취급합니다.
편미분 개념은 어떤 기계 장치의 온도가 기계로 들어가는 교류 실효값뿐만 아니라 압력에도 의존한다고 생각해봐요. 그러면 실효값과 압력이 달라지면 온도가 달라지는거에요.
이때 압력을 고정하고, 즉 압력을 상수로 취급하고 실효값에 따른 온도의 기울기를 구하는 방법이 편미분입니다. 물론 실효값을 상수로서 고정하고 압력에 따른 온도의 기울기를 구하는 것도 편미분입니다.
편미분의 기호는 다음과 같습니다. 예를 들어 변수가 여러개인 함수 f를 x로 편미분하고자 한다면 아래와 같이 쓰면 됩니다.
\tag{5}
{{\partial{f}}\over{\partial x}},~~f_x[예제3] 편미분
f(x,y)=3x^3 y+ 2x y^3 + 3x + 7y로서 독립 변수 x와 y에 의존하는 함수가 있다. 이 함수를 x와 y에 관해 각각 편미분하여라.
[풀이]
먼저 x에 관해 편미분부터 하면, y를 상수로 취급하면 됩니다. 이때 상수를 미분하면 0이 되는 것을 상기하세요.
\tag{E-3}
\begin{align}
{{\partial f}\over{\partial x}} &= {{\partial}\over{\partial x}}(3x^3 y+ 2x y^3 + 3x + 7y)\\
&=9x^2 y+2 y^3 +3
\end{align}다음에는 y에 관해 편미분하면 x를 상수로 취급하면 됩니다.
\tag{E-4}
\begin{align}
{{\partial f}\over{\partial y}} &= {{\partial}\over{\partial y}}(3x^3 y+ 2x y^3 + 3x + 7y)\\
&=3x^3 + 6xy^2 +7
\end{align}2. 미분방정식 (Differential equation)
미분방정식이란 ‘하나 또는 그 이상의 독립변수에 관하여 하나 또는 그 이상의 종속변수의 도함수 또는 미분을 포함하는 방정식’을 말합니다.
특히 독립변수가 하나인 경우 상미분방정식(상미방, ODE, Ordinary Differential Equation), 두개 이상인 경우 편미분방정식(편미방, PDE, Partial Differential Equation)이라고 부릅니다.
2-1. 상미분방정식
상미분방정식의 예시는 다음과 같습니다.
\tag{6}
{{d^2y}\over{dx^2}} + {{dy}\over{dx}} + \sin y =0(6)식을 보시면 y를 x로 미분하는 dy/dx항이 수식에 포함된 것을 볼 수 있어요.
이렇게 주어진 미분방정식을 푼다는 말은 독립변수가 x이고 종속변수가 y인 함수 y=f(x)를 구한다는 의미로 보시면 됩니다.
2-2. 편미분방정식
편미분방정식의 예시는 다음과 같습니다.
\tag{7}
{{\partial u}\over{\partial t}} = {{\partial^2 u}\over{\partial x^2}} +{{\partial^2 u}\over{\partial y^2}}(7)식을 보시면 u를 t로 편미분, u를 x로 편미분, u를 y로 편미분하는 내용이 포함된 방정식임을 알 수 있어요.
이렇게 주어진 편미분방정식을 푼다는 말은 독립변수가 x, ~y,~ t이고 종속변수가 u인 함수 u=f(x,y,t)를 구한다는 의미로 보시면 됩니다.
3. 미분방정식 구분
미분방정식은 다양한 모양을 가질 수가 있어요. 미분을 2번하는 방정식, 3번하는 방정식도 있을 수 있고 상미분과 편미분으로 구성된 방정식도 있을 수 있어요.
그래서 미분방정식을 구분하기 위한 이름이 있어야 합니다. 이때 사용되는 것이 미분방정식의 ‘계수’와 ‘차수’, ‘선형’과 ‘비선형’입니다.
3-1. 계수와 차수, 선형과 비선형
계수란 미분방정식에 포함되는 최고계 도함수의 계수를 말합니다.
미분이 한번인 dy / dx는 1계, {d^2}y / d{x^2}는 2계가 됩니다. 미분방정식에서 주어지는 도함수의 가장 큰 계수를 기준으로 이름이 붙습니다.
또한 차수란 미분방정식에 포함되어 있는 최고계 도함수의 지수를 말합니다.
예를 들어 (y^{\prime \prime \prime})^3은 지수가 3이므로 3차가 됩니다.
선형 미분방정식은 종속변수와 그 도함수가 1차이고 각 계수가 독립변수에만 의존하는 것을 말합니다.
이에 비해 비선형 미분방정식은 종속변수와 그 도함수가 지수를 갖거나 계수가 종속변수를 포함하거나, 비선형 함수 등을 포함하는 경우를 말합니다.
3-2. 미분방정식 구분의 예
\tag{8}
x {{dy}\over{dx}} + y =0~~~\rightarrow ~~1계~1차~선형~ 상미분방정식\tag{9}
x^3 {{d^3 y}\over{dx^3}} - 5x {{dy}\over{dx}}+ 8y =0~~~\rightarrow ~~3계~1차~선형~ 상미분방정식\tag{10}
4 (y^{\prime \prime \prime})^3 + 5x^3 (y^{\prime})^7 + 4y =0~~\rightarrow ~~3계~3차~비선형~상미분방정식(10)식에서 3계 도함수가 3제곱이므로 3차 미분방정식이 되며, 또한 이 때문에 도함수가 1차가 아니므로 비선형이 됩니다. 차수는 최고계 도함수를 기준으로 결정된다는 것을 기억하세요.
\tag{11}
\Big({{d^2 y}\over{dx^2}}\Big)^4 = \Big[1+\Big({{dy}\over{dx}}\Big)^2 \Big]^3~~\rightarrow~~2계~4차~비선형~상미분방정식\tag{12}
{{\partial ^3 u}\over{\partial x^3}}+(1-{\color{red}u^2}) =0~~\rightarrow~~3계~1차~{\color{red}비선형}~편미분방정식(12)식에서 종속변수인 u가 제곱(즉, 2차)의 형태여서 1차가 아니므로 비선형 방정식이 됩니다.
\tag{13}
{\color{red}(1-y)} {{dy}\over{dx}} + 4y = e^x~~\rightarrow~~1계~1차~{\color{red}비선형}~상미분방정식(13)식은 계수 (1-y)가 종속변수를 포함하여 독립변수만으로 구성되어 있지 않으므로 비선형이 됩니다.
\tag{14}
{{dy}\over{dx}} + {\color{red}\cos y} =0~~\rightarrow~~1계~1차~{\color{red}비선형}~상미분방정식(14)식은 종속변수가 비선형함수로서 1차가 아니므로 비선형이 됩니다.


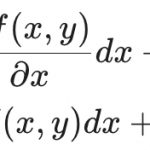



3 thoughts on “미분방정식 기초”