Last Updated on 2024-01-26 by BallPen
복소수의 다양한 표현법과 연산법, 그리고 관련 공식들을 알아봐요.
복소수(complex numbers)란 실수와 허수가 결합된 수 체계입니다. 기호로 쓰면 다음과 같아요.
\tag{D1}
x+iy여기서 x는 실수부(real part)라고 부르며, 허수 iy중 y를 허수부(imaginary part)라고 부릅니다.
이번 글에서는 복소수를 표현하는 다양한 방식과 복소수의 연산, 그리고 여러 관련 공식들을 알아보겠습니다.
볼펜을 잡고 하나씩 하나씩 직접 정리하며 풀어보세요.
아래는 이번 글의 목차입니다.
Contents
1. 복소수
1-1. 복소수의 표현
복소수는 복소 평면(complex plane)에서 표현될 수 있습니다. 여기서 복소 평면이란 복소수의 크기와 위치를 표현하는 특별한 평면 공간을 말해요.
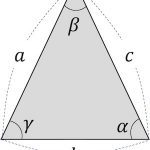
실수는 실수선이라 불리는 가로선 위에 모든 실수들이 배치되는 것에 비해 복소수는 복소 평면위에 배치돼요. 아래 [그림 1]은 복소평면을 나타낸 것입니다.
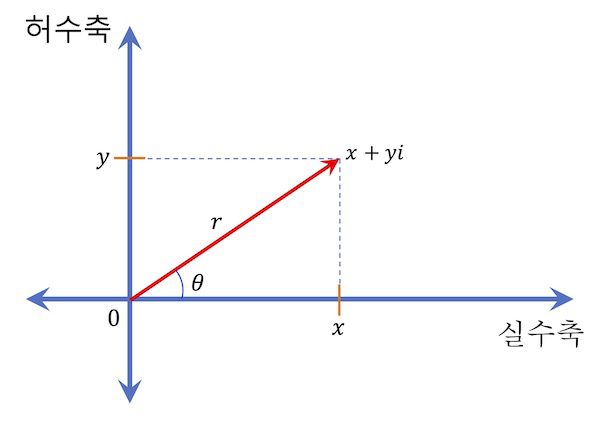
![[그림 1] 복소수 표현을 위한 복소 평면](https://ballpen.blog/wp-content/uploads/2024/01/Picture1-3-1024x732.jpg)
복소 평면의 가로축은 실수축이고 세로축은 허수축이에요. 이때 복소수의 실수부가 x이고 허수부가 y일때 복소수 z는 아래 (1-1)식과 같이 표현됩니다.
\tag{1-1}
z = x + iy한편 [그림 1]을 보면 복소수 z의 실수부는 x = r \cos \theta이고 허수부는 y=r \sin \theta에요.
따라서 (1-1)식은 다음과 같이 바꾸어 표현할 수도 있어요. 이러한 형태를 복소수의 극형식(polar form)이라고 부릅니다.
\tag{1-2}
\begin{align}
z &= x+iy\\
&=r \cos \theta + ir\sin \theta\\
&=r(\cos \theta + i\sin \theta)
\end{align}1-2. 복소수의 크기
복소수는 보통 (1-1)식과 (1-2)식으로 표현하는데요. 그 복소수의 크기 |z|는 [그림 1]에서 빨강색 화살표의 길이 r를 의미해요.
그래서 복소수의 실수부 x와 허수부 y를 피타고라스(Pythagoras) 정리에 대입하면 다음과 같이 그 크기 |z|를 구할 수 있어요.
\tag{1-3}
\begin{align}
|z| &= \sqrt{x^2 + y^2}\\[5pt]
&=\sqrt{r^2\cos^2 \theta + r^2 \sin^2 \theta}\\[5pt]
&=r\sqrt{\cos^2 \theta + \sin^2 \theta}\\[5pt]
&=r
\end{align}한편 복소수의 크기는 켤레복소수(complex conjugate)를 이용해 복소수를 실수화하는 방식으로도 구할 수 있어요.
이번에는 그 방법을 알려드릴게요.
어떤 복소수를 z=x+iy라 할 때 켤레복소수는 \bar z = x- iy로 정의됩니다. 따라서 켤레복소수는 허수부 y값의 부호만 바뀌므로 [그림 1]에 있는 화살표가 x축 대칭으로 바뀌는 것을 기하학적으로 상상하면 됩니다.
켤레복소수는 복소공액이라고 불리기도 해요.
그렇다면 복소수의 크기를 어떻게 구할 수 있을까요? 바로 복소수와 그 켤레복소수를 서로 곱하면 됩니다. 그 결과를 살펴보면 아래 (1-4)식과 같아요.
\tag{1-4}
\begin{align}
z \bar z &= (x+iy)(x-iy)\\
&=(x)^2 - ixy+ixy - (iy)^2\\
&=\color{blue}x^2 + y^2\\
&=|z|^2
\end{align}위 식의 세번째 줄은 (1-3)식 첫번째 줄의 양변을 제곱한 것과 같아요. 결국 복소수와 그 켤레복소수를 곱하면 복소수 크기를 제곱한 값과 같습니다.
그 관계를 다시 쓰면 다음과 같아요.
\tag{1-5}
r=|z| = \sqrt{z \bar z}2. 오일러 공식(Euler’s formula)
테일러급수는 어떤 함수를 다항식의 형태로 표현하는 방법을 말해요. 그중에서 \sin \theta, \cos \theta, e^{\theta}를 전개해보면 다음과 같아요.
\tag{2-1}
\begin{align}
&\sin \theta = \theta - {{\theta^3}\over{3 !}} + {{\theta^5}\over{5!}}- \cdots\\[10pt]
&\cos \theta = 1 - {{\theta^2}\over{2!}} + {{\theta^4}\over{4!}}-\cdots\\[10pt]
&e^\theta = 1 + \theta + {{\theta^2}\over{2!}} +{{\theta^3}\over{3!}} + \cdots
\end{align}이때 세번째 줄에 있는 e^\theta를 e^{i\theta}로 변경하여 정리해보면 다음이 됩니다.
\tag{2-2}
\begin{align}
e^{i \theta} &= 1+(i\theta) + {{(i\theta)^2}\over{2!}} + {{(i \theta)^3}\over{3!}} + {{(i \theta)^4}\over{3!}}+\cdots\\[10pt]
&=1+i\theta - {{\theta^2}\over{2!}} - {{ i\theta^3}\over{3!}} + {{ \theta^4}\over{4!}}+{{ i\theta^5}\over{5!}}+\cdots\\[10pt]
&=\Big(1 - {{\theta^2}\over{2!}} + {{\theta^4}\over{4!}}-...\Big)+i\Big( \theta - {{\theta^3}\over{3 !}} + {{\theta^5}\over{5!}}- \cdots\Big)\\[10pt]
&=\cos \theta + i \sin \theta\\[10pt]
\end{align}결국 e^{i\theta}는 다음과 같이 표현됩니다. 이 식을 오일러 공식이라고 불러요.
\tag{2-3}
e^{\pm i \theta} = \cos \theta \pm i \sin \theta위식에서 \theta는 [그림 1]처럼 기준축으로부터의 회전 각도인 ‘위상’을 의미해요. 때로는 위상을 ‘편각’이라고 부르기도 합니다.
그런데 오일러 공식을 잘 보면 (1-2)식 z=r(\cos \theta + i \sin \theta)의 괄호 안과 같다는 것을 알 수 있어요.
따라서 오일러 공식을 이용해 복소수 z를 극형식으로 표현해보면 다음과 같아요.
\tag{2-4}
z =x\pm iy= r(\cos \theta \pm i \sin \theta)=r e^{\pm i\theta}
복소수를 표현하는 다양한 방식이 있음을 알 수 있어요.
3. 복소수 연산
3-1. 복소수의 덧셈과 뺄셈
두 복소수를 더하고 빼는 방법은 다음과 같아요. 실수부는 실수부끼리, 허수부는 허수부끼리 더해주거나 빼주면 됩니다.
\tag{3-1}
(x_1 + iy_1) \pm(x_2+iy_2)= (x_1 \pm x_2) + i(y_1 \pm y_2)[예제1]
(3+i4)와 (5+i6)의 두 복소수를 합하여라.
(sol) 위 (3-1)식을 적용하여 계산하면 됩니다.
\tag{ex-1}
(3+i4)+(5+i6) = (3+5)+i(4+6) = 8+i10만일 두 복소수를 빼고 싶다면 다음과 같이 계산하세요.
\tag{ex-2}
(3+i4)-(5+i6) = (3-5)+i(4-6) = -2-i23-2. 복소수의 곱
두 복소수의 곱셈은 서로 전개하여 구하거나 다음의 관계를 활용하면 됩니다.
복소수 z_1 = r_1 e^{i \theta_1}과 z_2 = r_2 e^{i \theta_2}가 있어요. 이 두 복소수를 곱해 봐요.
\tag{3-2}
\begin{align}
z_1 \cdot z_2 &= r_1 e^{i\theta_1} \cdot r_2e^{i\theta_2} \\[5pt]
&=r_1 r_2 e^{i(\theta_1 + \theta_2)}
\end{align}위 식과 같이 두 복소수를 곱하면 복소수 크기는 서로 곱해지고 위상은 서로 합해지는 특성이 있어요.
[예제2]
(3+i4)와 (3+i4)의 두 복소수를 곱하여라.
(sol) 두개의 해법이 있습니다. 하나는 전개하여 구하는 방법과 다른 하나는 (3-2)식을 활용하는 거에요.
우선 전개하는 방법으로 구해봐요.
\tag{ex-3}
\begin{align}
(3+i4)(3+i4) &= 9+i12+i12+16i^2\\
&=9+i24-16\\
&=-7+i24
\end{align}이번에는 (3-2)식을 적용해봐요. 이때 (3+i4)의 위상은 \cos \theta = {{x}\over{r}}이므로 \theta = \cos^{-1} {{x}\over{r}}입니다.
\tag{ex-4}
\begin{align}
(3+i4)(3+i4) &= \big(\sqrt{3^2 + 4^2}e^{i\cos^{-1}{{3}\over{\sqrt{3^2 + 4^2}}}}\Big) \big(\sqrt{3^2 + 4^2}e^{i\cos^{-1}{{3}\over{\sqrt{3^2 + 4^2}}}}\Big)\\
&=5e^{i53.1^{\circ}}5e^{i53.1^{\circ}}\\
&=25e^{i106.2^{\circ}}\\
&=25(\cos {106.2^{\circ}} + i\sin 106.2^{\circ})\\
&=-7+i24
\end{align}두 결과가 서로 같다는 것을 알 수 있어요.
3-3. 복소수의 나눗셈
두 복소수가 분수로 표현된 경우 이를 단일의 복소수로 정리할 필요가 있어요. 그때는 분모에 있는 복소수의 켤레복소수를 분모와 분자에 모두 곱하여 분모를 실수화한 후 정리합니다.
바로 예제를 하나 풀어보겠습니다.
[예제3]
(3+i)를 (2+i)로 나누어라.
(sol) 분모에 있는 복소수의 켤레복소수를 분자와 분모에 모두 곱해줍니다.
\tag{ex-5}
\begin{align}
{{3+i}\over{2+i}} &= {{(3+i)\color{red}(2-i)}\over{(2+i)\color{red}(2-i)}} \\[10pt]
&={{6-i3 + i2 - i^2}\over{2^2 -i^2}}\\[10pt]
&={{7-i}\over{4+1}}\\[10pt]
&={7 \over 5} - i{1 \over 5}
\end{align}
3-4. 복소수의 거듭제곱
복소수 z=re^{i\theta}의 n제곱은 다음과 같이 표현할 수 있을거에요.
\tag{3-3}
z^n = (re^{i \theta})^n = r^n (e^{in\theta})이때 (3-3)식의 가운데 항은 다음과 같이도 표현될 수 있어요.
\tag{3-4}
z^n = (re^{i \theta})^n = r^n (e^{i \theta})^n = r^n(\cos \theta + i \sin)^n또한 (3-3)식의 가장 오른쪽 항은 다음 관계도 성립할거에요.
\tag{3-5}
\begin{align}
z^n = r^n(e^{in \theta}) = r^n (\cos n\theta + i \sin n\theta)
\end{align}이때 (3-3)식에 따라 (3-4)과 (3-5)식은 서로 같아야 하므로 결국 다음 관계가 성립합니다.
\tag{3-6}
z^n = r^n(\cos \theta + i \sin \theta)^n = r^n(\cos n \theta + i \sin n \theta)한편 복소수에 1 \over n승을 취하면 (3-6)식은 다음과 같이 표현됩니다.
\tag{3-6}
z^{1 \over n} = r^{1 \over n}(\cos \theta + i \sin \theta)^{1\over n} = r^{1 \over n}(\cos {\theta \over n} + i \sin {\theta \over n})[예제4]
8의 세제곱근을 복소수 범위에서 모두 구하여라.
(Sol) 복소수 범위에서 8의 세제곱근은 총 3개의 해가 나옵니다. 일단 8의 세제곱은 8^{1/3}로 쓸 수 있는데요.
이를 복소수로 확장하기 위해 8^{1/3} (e^{ix})^{1/3}로 표현해 볼게요.
그러면 다음과 같이 ix=0,~i2\pi, ~i4\pi가 되면 e^0 = e^{i2\pi} = e^{i4\pi}=1이 된다는 것을 알 수 있어요.
결국 아래와 같이 한 개의 해는 실수이고, 다른 두개의 해는 복소수가 나오게 되는거에요. (3-6)식을 적용하여 정리하면 다음과 같습니다.
\tag{ex-6}
\begin{align}
8^{1/3} = 8^{1/3}(e^{x})^{1/3} &= 2(e^{0})^{1/3}=2 (\cos{0 \over 3} + i\sin{0 \over 3})=2\\
&=2(e^{i2 \pi })^{1/3} = 2\Big(\cos{{2\pi}\over{3}} + i \sin{{2\pi}\over{3}}\Big)=-1+i\sqrt{3}\\
&=2(e^{i4 \pi })^{1/3} = 2\Big(\cos{{4\pi}\over{3}} + i \sin{{4\pi}\over{3}}\Big)=-1-i\sqrt{3}
\end{align}다시 한번 더 말씀드리면 위 식에서 e^0, e^{i2\pi}, e^{i4\pi}는 (2-3)식의 오일러 공식을 적용해보면 모두 1이 나오는 것을 알 수 있어요. 예를 들어 e^{i2\pi} = \cos(2\pi)+i\sin (2 \pi) =1이 되는 원리입니다.
또한 e^{i6\pi}, e^{i8\pi} 등도 있을 수 있지만 그 값들을 구해보면 (ex-6)식에서 도출된 세개의 값이 반복될 뿐입니다.
한편, 식에서 나온 \cos{{2\pi}\over{3}}, \sin {{4\pi}\over{3}}의 값들을 구하는 방법이 궁금하면 여기를 클릭하세요.
4. 복소 삼각함수, 복소 쌍곡선함수, 복소 로그함수
4-1. 복소 삼각함수
\cos \theta, \sin \theta, \tan \theta가 복소수로 어떻게 표현되는지 알아봐요.
e^{i\theta}와 e^{-i\theta}를 서로 합하면 다음과 같아요.
\tag{4-1}
\begin{align}
e^{i\theta} + e^{-i\theta} = (\cos \theta + i \sin \theta) + (\cos \theta - i \sin \theta) = 2 \cos \theta
\end{align}위 (4-1)식을 \cos \theta에 대해 정리하면 다음이 성립합니다.
\tag{4-2}
\cos \theta = {{e^{i \theta}+e^{-i \theta}}\over{2}}이번에는 e^{i\theta}와 e^{-i\theta}를 서로 빼면 다음과 같아요.
\tag{4-3}
\begin{align}
e^{i\theta} - e^{-i\theta} = (\cos \theta + i \sin \theta) - (\cos \theta - i \sin \theta) = 2i\sin \theta
\end{align}위 (4-3)식을 \sin \theta에 대해 정리하면 다음과 같아요.
\tag{4-4}
\sin \theta = {{e^{i \theta}-e^{-i \theta}}\over{2i}}다음에서 \tan \theta를 구해봐요.
\tag{4-5}
\begin{align}
\tan \theta &= {{\sin \theta}\over{\cos \theta}}\\[10pt]
&={{(e^{i \theta} - e^{-i\theta})/2i}\over{(e^{i\theta}+e^{-i\theta})/2}}\\[10pt]
&={{e^{i\theta}-e^{-i\theta}}\over{i(e^{i\theta}+e^{-i\theta})}}
\end{align}위식에서 분자와 분모에 i를 곱하면 다음과 같이 \tan \theta를 구할 수 있어요.
\tag{4-6}
\tan \theta = -i\Big({{e^{i\theta}-e^{-i\theta}}\over{e^{i\theta}+e^{-i\theta}}}\Big)4-2. 복소 쌍곡선함수
복소 쌍곡선함수를 다루기 전에 우선 쌍곡선함수를 정리하겠습니다. 그 이유는 복소 쌍곡선 함수를 구하기 위해서는 쌍곡선함수식이 필요하기 때문이에요.
쌍곡사인(hyperbolic sine), 쌍곡코사인(hyperbolic cosine), 쌍곡탄젠트(hyperbolic tangent)는 다음과 같아요.
\tag{4-7}
\begin{align}
\sinh x = {{e^x - e^{-x}}\over{2}}\\[10pt]
\cosh x = {{e^x + e^{-x}}\over{2}}\\[10pt]
\tanh x = {{e^x - e^{-x}}\over{e^x + e^{-x}}}
\end{align}그럼 이제부터 복소 쌍곡선함수를 정의하겠습니다.
우선 \sin ix를 구해봐요. (4-4)식의 \theta대신에 ix를 대입하면 됩니다. 그럼 다음이 성립할 거에요.
\tag{4-8}
\begin{align}
\sin ix &= {{e^{i (ix)}-e^{-i (ix)}}\over{2i}}\\[10pt]
&={{e^{-x} - e^{x}}\over{2i}}\\[10pt]
&=i{{e^x - e^{-x}}\over{2}}\\[10pt]
&=i \sinh x
\end{align}이번에는 \cos ix를 구해봐요. (4-2)식의 \theta대신에 ix를 대입하면 됩니다.
\tag{4-9}
\begin{align}
\cos ix &= {{e^{i (ix)}+e^{-i (ix)}}\over{2}}\\[10pt]
&={{e^{-x} + e^{x}}\over{2}}\\[10pt]
&=\cosh x
\end{align}마지막으로 \tan ix를 구해봐요.
\tag{4-10}
\tan ix = {{\sin ix}\over{\cos ix}} = {{i \sinh x}\over{\cosh x}} = i \tanh x4-3. 복소 로그함수
복소수 z가 있을 때 다음의 관계가 성립한다고 생각해봐요. 물론 z \ne 0입니다.
\tag{4-11}
z = e^\omega양변에 자연로그 \ln을 취한 후 \omega에 대해 정리하면 다음의 관계가 성립합니다. 이때 복소수 z는 (2-4)식을 이용하여 z=re^{i \theta} 를 대입합니다.
\tag{4-12}
\begin{align}
w = \ln z &= \ln (re^{i \theta})\\
&=\ln r + \ln e^{i \theta}\\
&=\ln r + i \theta
\end{align}[예제5] ln(1+i)
\ln (1+i)를 복소수로 나타내어라.
(sol) (4-12)식을 그대로 적용하면 됩니다. 이때 (1+i)의 크기는 다음과 같습니다.
\tag{ex-7}
\begin{align}
r &= \sqrt{x^2+y^2}\\
&=\sqrt{1^2+1^2} \\
&= \sqrt{2}
\end{align}또한 (1+i)는 실수축으로 1, 허수축으로 1이므로 편각 \theta는 다음과 같습니다.
\tag{ex-8}
\cos \theta = {x \over r} = {1 \over {\sqrt{}2}}따라서 \theta = {\pi \over 4}이므로, 최종 답은 다음과 같습니다.
\tag{ex-9}
\begin{align}
\ln (1+i) &= \ln(\sqrt{2} e^{{i\pi} / 4 })\\
&=\ln{\sqrt{2}} + i{\pi \over 4}
\end{align}[예제6] ln(-1)
\ln (-1)를 복소수로 나타내어라.
(sol) 실수에서 \ln(-1)은 값이 존재하지 않아요. 하지만 복소수로 범위를 넓히면 그 값이 존재합니다. 그것을 구해봐요.
우선 다음의 식이 성립함을 우리는 알고 있어요.
\tag{ex-10}
-1 = e^{i\pi}왜냐하면 e^{i\pi}는 \cos\pi + i \sin \pi=\cos \pi +0= -1이기 때문이에요.
따라서 정답은 다음과 같습니다.
\tag{ex-11}
\begin{align}
\ln(-1) &= \ln(e^{i \pi})\\
&=\ln 1 + \ln e^{(i\pi)}\\
&=0+i\pi\\
&=i\pi
\end{align}[예제7] ln(i)
\ln (i)를 복소수로 나타내어라.
(sol) 이 문제는 위 [예제6]과 동일한 방식으로 풀면 됩니다. 잘 생각해보면 i는 다음의 관계가 성립함을 알 수 있어요.
\tag{ex-12}
i = e^{i\pi/2}왜냐하면 e^{i\pi /2}는 \cos(\pi/2) + i \sin (\pi/2)이기 때문이에요.
따라서 정답은 다음과 같습니다.
\tag{ex-13}
\begin{align}
\ln(i) &= \ln(e^{i \pi/2})\\
&=\ln 1 + \ln e^{(i\pi/2)}\\
&= 0+{{i\pi} / 2}\\
&=i{{\pi}\over 2}
\end{align}