Last Updated on 2024-01-06 by BallPen
전미분이란 무엇이고 완전미분방정식은 어떻게 푸는지 알아봐요.
완전미분방정식(exact differential equation)이란 변수가 2개 이상인 다변수 함수의 전미분 형태로 주어진 미분방정식을 말합니다.
말이 좀 어렵죠. 그러나 아래 내용을 읽어보시면 충분히 이해할 수 있어요.
이전 글에서 설명드린 변수분리형 미분방정식 해법과는 또 다른 즐거움을 느낄 수 있습니다.
함께 알아봐요.
아래는 이번 글의 목차입니다.
Contents
1. 전미분
완전미분방정식을 이해하기 위해서는 전미분(total differential)부터 알아야 합니다.
전미분을 계산하기 위해서는 편미분이 활용됩니다. 변수가 하나인 상미분과는 달리 전미분은 변수가 2개 이상인 경우에 정의되기 때문입니다.
전미분, 편미분, 상미분의 개념을 명확히 구분할 줄 알아야 해요. 전미분은 이번 글을 참고하시고 편미분과 상미분은 이전 글을 참고해 주세요.
전미분에 대한 이야기를 이어갑니다.
1-1. 전미분 정의
변수가 2개 이상인 함수를 다변수 함수라고 해요. 예를 들어 변수 x와 변수 y를 갖는 어떤 함수 f=f(x,y)가 있어요.
즉, 이 함수의 함수값 f는 x가 변해도 달라지고, y가 변해도 달라져요.
이때 변수 x와 y만의 변화에 따른 f의 변화율인 편미분 {\partial {f} \over {\partial{x}}}, {\partial {f} \over {\partial{y}}}에 각각의 미소변화량 dx, dy를 곱한 후 서로 합한 것이 함수 f의 미소변화량 df와 같아요.
이것을 식으로 표현하면 다음과 같습니다.
\tag{1}
\color{red}df = {{\partial f}\over{\partial x}} dx + {{\partial f}\over{\partial y}} dy 바로 (1)식을 전미분 또는 완전미분(exact differential)이라 부릅니다.
그렇다면 이 식이 뜻하는 의미는 무엇일까요? 쉽게 예를 들어 설명하겠습니다.
어떤 기계 장치를 생각해봐요. 이 기계장치에는 통이 달려있는데, 이 통 안의 온도가 압력과 전압에 의존한다고 가정하겠습니다.
그러니까 통안의 온도를 올리고 싶으면 압력을 증가시키거나 또는 전압을 증가시키면 되는거에요.
그런데 통 안의 온도가 현재 20 ^{\circ} \mathrm{C}라고 가정할 때 압력을 현재보다 200 kPa 만큼 더 증가시키고, 전압도 100 V 만큼 더 증가시킨다면 통 안의 온도는 몇 도 증가할까요? 단, 압력이 50 kPa 증가할 때 통안의 온도는 3 ^{\circ} \mathrm{C} 증가하고, 전압이 10 V 증가할 때 통 안의 온도는 2 ^{\circ} \mathrm{C}씩 증가합니다.
그러면 사람들은 다음의 식을 세우고 문제를 풀게 됩니다.
\tag{2}
\begin{align}
증가한~온도 &= (단위~압력당~온도~변화율 \times 압력~변화량) +\\
&~~~~~~~~~~~~~~(단위~전압당~온도~변화율 \times 전압~변화량)
\end{align}\tag{3}
\begin{align}
dT &= \Big( {{3^{~\circ}\mathrm{C}}\over{50~\mathrm{\cancel{kPa}}}} \times 200~\mathrm{\cancel{kPa}} \Big)+\Big( {{2^{~\circ}\mathrm{C}}\over{10~\mathrm{\cancel{V}}}} \times 100~\mathrm{\cancel{V}} \Big)\\
&=12^{~\circ }\mathrm{C} + 20^{~\circ }\mathrm{C}\\
&=32^{~\circ }\mathrm{C}
\end{align}압력과 전압의 변화에 따른 온도 변화량은 32 ^{\circ}\mathrm{C}가 됩니다. 결국 통안의 온도는 최초 20^{\circ} \mathrm{C}에서 32^{\circ} \mathrm{C}가 증가되어 52^{\circ} \mathrm{C}가 됩니다.
이때 (2)식을 (1)식과 비교하면 ‘단위 압력당 온도변화율’과 ‘단위 전압당 온도변화율’은 (1)식의 편미분 부분에, 압력변화량과 전압변화량은 (1)식의 dx와 dy 부분에 해당합니다.
물론 (3)식에서의 dT는 (1)식의 df와 같습니다.
1-2. 전미분 예제
아래의 다변수 함수 f(x,y)가 있습니다.
\tag{4}
f(x,y) = 2xy + 3x + y + 1이 함수를 전미분하여 전도함수 df(x,y)를 구해보겠습니다.
\tag{5}
\begin{align}
df(x,y) &= {{\partial f(x,y)} \over{\partial x}} dx + {{\partial f(x,y)}\over{\partial y}} dy\\
&= (2y + 3) dx + (2x+1)dy
\end{align}2. 완전미분방정식
2-1. 완전미분방정식 정의와 개념
변수가 2개인 어떤 이변수 함수 f(x,y)가 있을 때 이 함수의 전미분은 다음과 같습니다.
\tag{6}
\begin{align}
df(x,y) &={\partial f(x,y) \over \partial x} dx + {\partial f(x,y) \over \partial y} dy\\
&=M(x,y) dx + N(x,y)dy
\end{align}
여기서 M(x,y)와 N(x,y)는 f(x,y)를 x와 y로 편미분한 것을 나타내는 기호입니다.
이때 (6)식이 다음 관계를 만족하면 그것을 ‘완전미분방정식’이라고 부릅니다.
\tag{7}
\color {red}M(x,y)dx + N(x,y)dy =0물론 (7)식이 성립한다는 의미는 df(x,y)=0을 뜻하고, 이 말은 아래 (8)식처럼 f(x,y)가 값이 변하지 않는 상수임을 뜻합니다.
\tag{8}
f(x,y) = C또한 중요한 성질이 하나 더 있는데요. 바로 다음의 식이 성립합니다.
\tag{9}
\begin{align}
{{\partial M(x,y)}\over{\partial y}} &= {{\partial N(x,y)}\over{\partial x}}\\
\end{align}이 (9)식이 성립하는 이유는 M(x,y)와 N(x,y)에 (6)식에 주어진 원래 편미분을 대입해 보면 알 수 있어요.
\tag{10}
\begin{align}
{{\partial M(x,y)}\over{\partial y}} &= {{\partial ({\partial f(x,y)/\partial x)}}\over{\partial y}}= {\color{blue}{{\partial^2 f(x,y)}\over{\partial y \partial x}}} \\
&= {{\partial N(x,y)}\over{\partial x}} = {{\partial (\partial f(x,y)/\partial y)}\over{\partial x}}= {\color{blue}{{\partial^2 f(x,y)}\over{\partial x \partial y}}}\\
\end{align}이때 다변수함수를 x로 먼저 편미분하던 y로 먼저 편미분 하던 그 결과는 서로 같아요.
따라서 (9)식이 성립함을 알 수 있어요.
그러므로 주어진 미분방정식이 완전미분방정식인지의 여부를 판정하기 위해 (9)식의 관계를 활용할 수 있어요.
그렇다면 이제부터 완전미분방정식의 해법을 설명드립니다.
2-2. 완전미분방정식 풀이 방법
아래에 미분방정식이 있어요. 이 미분방정식의 풀이 방법을 단계별로 설명드립니다.
\tag{11}
M (x,y) dx + N(x,y) dy = 0첫째, 주어진 미분방정식이 완전미분방정식인지의 여부를 판정해야 합니다. 만일 완전미분방정식이 아니면 이 방법으로 문제를 풀수 없어요.
(11)식이 완전미분방정식이 되기 위해서는 위 (9)식에서 설명드렸듯이 다음의 관계를 만족해야 합니다.
\tag{12}
\begin{align}
{{\partial M(x,y)}\over{\partial y}} &= {{\partial N(x,y)}\over{\partial x}}\\
\end{align}일단 주어진 방정식이 완전미분방정식으로 판정되었다고 하겠습니다.
둘째, 다음의 관계로부터 f(x,y)를 구합니다. 그리고 f(x,y)는 (8)식에서와 같이 상수가 되어야 합니다. 여기서는 그 상수를 C_1으로 표기하겠습니다.
\tag{13}
\begin{align}
{\partial f(x,y) \over \partial x} &= M(x,y)\\
d f(x,y) &= M(x,y) d x \\
\int df(x,y) &= \int M(x,y) dx + k(y)\\
\color {blue}f(x,y) & {\color{blue}= \int M(x,y) dx +k (y)} = C_1 \\
\end{align}
위 식에서 k (y)는 y만의 함수로 구성된 적분상수인데요. 첫번째 줄에서 x로 편미분한 것이 M(x,y)이므로 이를 적분하면 y만의 함수도 상수로 간주할 수 있어요.
잘 이해가 안가시면 (13)식의 파랑색 부분을 x로 편미분해보세요. 그러면 k (y)는 y만의 함수이므로 x로 편미분하면 0이 되어 첫번째 줄의 수식으로 귀결됨을 알 수 있어요.
셋째, 이번에는 다음 관계식을 이용해 k(y)를 구합니다. 이를 위해 (13)식의 마지막 파랑색 수식 부분을 활용합니다.
\tag{14}
\begin{align}
{\partial f(x,y) \over \partial y} &= N(x,y)\\
{\partial \over \partial y} \Big( \int M(x,y) dx \Big) +{dk(y) \over dy} &= N(x,y) \\
{{dk(y)}\over{dy}} &= N(x,y) - {\partial \over \partial y} \Big( \int M(x,y) dx \Big)\\
k(y) &= \int \Big[N(x,y) - {\partial \over \partial y} \Big( \int M(x,y) dx \Big) \Big]dy + C_1
\end{align}
이 과정에서 k (y)를 y로 미분할 때 편미분이 아닌 상미분으로 기호를 바꾸었습니다.
넷째, (14)식의 가장 마지막을 (13)식의 k(y)에 대입하고 정리합니다. 그러면 최종 해인 f(x,y)를 구할 수 있습니다.
절차가 다소 복잡해 보이지만 아래의 예제를 풀어보면 쉽게 할 수 있어요.
2-3. 완전미분방정식 예제1
아래 미분방정식의 해를 구해보세요.
\tag{q-1}
3x^2ydx +(x^3 -2) dy =0이 문제를 풀기 위해서는 3x^2y = M(x,y), (x^3 - 2) = N(x,y))로 치환하여 생각해보는 것이 중요합니다.
\tag{q-2}
M (x,y) dx + N(x,y) dy = 0이제부터 문제를 풀어보죠.
첫째, (12)식을 이용하여 문제에 주어진 미분방정식이 완전미분방정식인지의 여부를 판별해야 합니다.
\tag{q-3}
{{\partial M(x,y)}\over{\partial y}} = {{\partial (3x^2 y)}\over{\partial y}} = 3x^2\tag{q-4}
{{\partial N(x,y)}\over{\partial x}} = {{\partial (x^3 - 2)}\over{\partial x}} = 3x^2(q-3)과 (q-4)가 서로 동일하므로 문제에 주어진 식은 완전미분방정식이 맞습니다. 그렇다면 계속 순차적으로 풀어나가면 됩니다.
둘째, 다음의 관계를 이용해 f(x,y)=C_1를 구합니다.
\tag{q-5}
\begin{align}
{\partial f(x,y) \over \partial x} &= M(x,y) = 3x^2y\\
df(x,y) &= 3x^2y dx\\
\int df(x,y) &= \int 3x^2y dx \\
f(x,y) &= {{x^3 y}} + k(y) = C_1
\end{align}셋째, 이번에는 k(y)를 구합니다. 아래의 관계를 이용하세요.
\tag{q-6}
\begin{align}
{\partial f(x,y) \over \partial y} &= N(x,y) = x^3 - 2\\
{{\partial \Big( x^3 y + k(y)\Big)}\over{\partial y}} &= x^3 -2\\
\cancel{x^3} + {{dk(y)}\over{dy}} &= \cancel{x^3} - 2\\
dk(y) &= (- 2)dy\\
\int dk(y) &= \int - 2dy\\
k(y) &=- 2y + C_2
\end{align}넷째, 위에서 도출된 k(y)를 (q-5)식에 대입하고 정리하세요.
\tag{q-7}
\begin{align}
f(x,y) = x^3 y + k(y) = C_1\\
{x^3} y + (- 2y + C_2) = C_1\\
(x^3 -2) y = (C_1 - C_2)\\
(x^3 - 2 )y = C
\end{align}결국 해는 f(x,y)=(x^3 - 2)y = C입니다. 그런데 도출된 해가 정말 해인지 궁금하시죠?
도출된 해를 전미분해보세요.
\tag{q-8}
\begin{align}
df(x,y) &= {{\partial f(x,y)}\over{\partial x}} dx + {{\partial f(x,y)}\over{\partial y}}dy\\
&=3x^2 y dx + (x^3 -2) dy =0
\end{align}
문제에서 주어진 미분방정식과 동일한 형태가 얻어지는 것을 알 수 있습니다. 해가 맞군요.
2-3. 완전미분방정식 예제2
아래에 또 다른 미분방정식이 주어져 있어요. 이 미분방정식의 해를 구해보세요.
\tag{q-9}
(\cos x \sin x - xy^2 ) dx + y(1 - x^2 ) dy =0이 문제도 완전미분방정식일 수 있으니 \cos x \sin x - xy^2 = M(x,y) , y(1-x^2) = N(x,y)로 치환해보죠. 그러면 아래와 같습니다.
\tag{q-10}
M(x,y) dx + N(x,y) dy = 0그러면 문제를 풀어보죠.
첫째, 문제에 주어진 미분방정식이 완전미분방정식인지 판별해봐야겠죠? 이를 위해서 (12)식의 관계를 이용합니다.
\tag{q-11}
{{\partial M (x,y)}\over{\partial y}} = {{\partial (\cos x \sin x - xy^2)}\over{\partial y}} = -2xy\tag{q-12}
{{\partial N (x,y)}\over{\partial x}} = {{\partial (y(1-x^2))}\over{\partial x}} = -2xy(q-11)과 (q-12)가 서로 같아 (12)식이 성립함을 알 수 있습니다. 그러므로 문제에 주어진 방정식은 완전미분방정식입니다.
둘째, 다음의 관계를 이용해 f(x,y) = C_1 을 구합니다.
\tag{q-13}
\begin{align}
{{\partial f(x,y)}\over{\partial x}} &= M (x,y) = \cos x \sin x - xy^2\\
df(x,y) &= (\cos x \sin x - xy^2) dx\\
\int df(x,y) &= \int (\cos x \sin x - xy^2) dx
\end{align}이때 삼각함수의 두배각공식에 따라 \sin (2x) = \sin x \cos x + \cos x \sin x와 같으므로 \cos x \sin x = \sin(2x) / 2로 둘 수 있습니다.
그러므로 (q-13)식은 다음과 같이 표현될 수 있습니다.
\tag{q-14}
\begin{align}
f(x,y) &= \int \Big( {1 \over 2} \sin (2x) - xy^2 \Big) dx\\
&= -{{1}\over{4}} \cos (2x) - {{x^2}\over{2}}y^2 + k(y) = C_1
\end{align}셋째, 이번에는 y만의 함수로 주어지는 k(y)를 구해봐요.
\tag{q-15}
\begin{align}
{{\partial f(x,y)}\over{\partial y}} &= N(x,y) = y(1-x^2)\\
{{\partial}\over{\partial y}} \Big(-{1 \over 4} \cos (2x) - {{x^2}\over{2}} y^2 + k(y) \Big) &=y (1- x^2)\\
\cancel{-x^2 y} + {{dk(y)}\over{dy}} &= y - \cancel{ x^2 y}\\
dk(y) &= y dy\\
\int dk(y) &= \int y dy\\
k(y) &= {y^2 \over 2} + C_2
\end{align}넷째, 도출된 k(y)를 (q-14)식에 대입합니다.
\tag{q-16}
\begin{align}
- {1 \over 4} \cos (2x) - {x^2 \over 2} y^2 + {y^2 \over 2 } + C_2 = C_1\\
- {1 \over 4} \cos (2x) - {x^2 \over 2} y^2 + {y^2 \over 2 } = C_1 - C_2\\
- {1 \over 4} \cos (2x) - {x^2 \over 2} y^2 + {y^2 \over 2 } = C\\
\end{align}바로 (q-16)식의 마지막 줄이 해가 됩니다. 이번에도 정말 해인지 알아보기 위해 전미분을 해봐요.
\tag{q-17}
\begin{align}
df(x,y) &= {{\partial f(x,y)}\over{\partial x}} dx + {{\partial f(x,y)}\over{\partial y}}dy\\
&= \Big[\Big(-{ 1 \over 4}\Big)\Big(-{2}\sin (2x) \Big) - {{2x}\over{2}}y^2 \Big]dx + \Big[ -{{x^2}\over{2}} (2y) + {{2y}\over{2}} \Big]dy \\
&=\big({1 \over 2} \sin (2x) - xy^2 \big)dx + \big( -x^2 y + y \big) dy\\
&=({1 \over 2} 2 \sin x \cos x - xy^2) dx +y(1 - x^2)dy\\
&=(\cos x \sin x -xy^2) dx + y(1 -x^2) dy =0
\end{align}문제에서 주어진 미분방정식이 도출되어 해가 분명함을 알 수 있습니다.
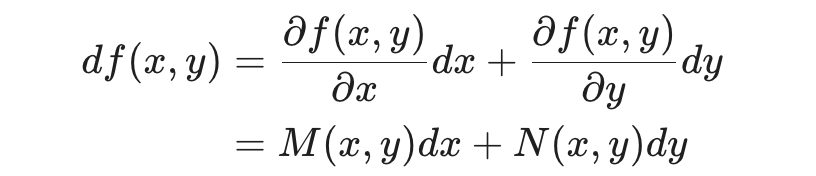
별점 5점인데 잘못 눌렀어요..
ㅎㅎㅎ 괜찮습니다. 방문해주셔서 감사합니다.
안녕하세요 좋은 게시물 감사합니다!
식(13) 부분의 첫번째 줄에서 두번째 줄로 넘어가는 부분이 이해되지 않아 질문 남깁니다..!
DH님 방문해주셔서 감사합니다. 응답이 늦어 죄송합니다.
식(13)에서 첫분째 줄이 두번째줄로 바뀐 것은, 원래 첫번째 줄은 함수 f에 대해 y를 상수로 두고 x로 미분하는 편미분이잖아요. 그래서 y가 상수라는 것을 우리가 알고 있다는 전제하에 이를 상미분으로 표현을 바꾼것입니다. 그러면 df/dx=M 인데요. 이의 형태를 바꾸어서 df=Mdx로 바꾼것입니다. 또한 y가 상수라는 것을 우리가 알고 있으므로 세번째 줄에서 적분상수를 y만의 함수로 두고 식을 정리해 나갔던 것입니다.