평균의 평균, 과연 전체 평균과 같을까요?

BallPen · 2022-05-27T06:30:00+09:00

평균의 평균값이 전체 평균값과 같은지 궁금할 때가 있어요. 예를들어 반별 학생수가 동일한 경우 각 반으로부터 구한 평균의 평균 점수는 전체학생의 평균 점수와 같아요. 그러나 반별 학생수가 다른 경우 반별 평균의 평균점수는 전체 평균점수와는 달라집니다.

Last Updated on 2023-01-21 by BallPen

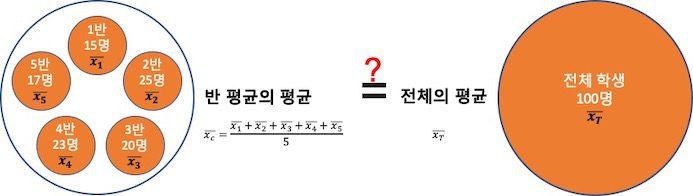
반별 평균의 평균값이 전체 학생의 평균값과 같을까요? 고민스러운 질문인데요. 함께 알아봐요.

평균의 평균 값이 전체 평균 값과 같은지 궁금할 때가 있습니다.

예를들어 어느 학교에 1반 부터 5반까지 있을때 전체 학생의 과학시험 성적의 평균을 구한다고 상상해 보세요. 이때 각 반의 평균값을 먼저 산출한 후 그 평균 값들의 평균을 내면 과연 전체학생의 평균 값과 같을까요?

같을 것 같기도 하고, 다를 것 같기도 해요.

결론부터 말씀드리면 특별한 경우를 제외하고는 다른 값이 나옵니다.

그 이유를 알아봐요. 아래는 이번 글의 목차입니다.

Contents

1. 평균
2. 평균의 평균
- 2-1. 각 반의 학생수가 동일한 경우
- 2-2. 각 반의 학생수가 다른 경우
3. 평균의 평균 값과 전체 평균 값이 일반적으로 다르다는 증명

1. 평균

어느 집단의 수치 크기에 대한 대표값을 구하기 위해 평균을 많이 사용합니다. 평균은 상황에 따라 산술평균, 기하평균, 조화평균이 사용될 수 있는데요. 이에 대한 구체적인 구분과 사용사례는 이전 글을 참고하시기 바랍니다. 아니면 위키백과를 참고하는 것도 좋아요.

이번 글에서는 보통 주로 사용 되는 산술평균에 대해 잠시 이야기 하겠습니다.

산출평균 $\bar x$ 은 대상 집단의 데이터 값들을 $x_i$ , 데이터의 갯수를 $n$ 이라고 했을 때 다음 식으로 구할 수 있어요.

\tag{1} \begin{align} \bar x = {{\sum x_i}\over{n}} \end{align}

예를 들어, 총 100명의 학생이 있다고 보세요. 그리고 1번 학생은 과학시험에서 1점, 2번 학생은 2점, 3번 학생은 3점과 같은 방식으로 점수를 얻었어요. 따라서 76번 학생은 76점, 92번 학생은 92점, 100번 학생은 100점을 얻은 거죠.

이 경우 전체 학생의 과학시험 평균값 $\bar x$ 는 아래 (2)식과 같이 50.5점이 됩니다.

\tag{2} \begin{align} \bar {x} &= {{1+2+3+\cdots +98+ 99+100}\over{100}}\\ &=50.5 \end{align}

2. 평균의 평균

이제부터 각 반에서 구한 평균의 평균 값이 전체 평균 값과 같은지의 여부를 함께 알아봐요.

구체적 계산을 위해 위 예시와 같이, 1반부터 5반까지의 총 학생수는 100명이라고 가정해볼께요. 그리고 1번 학생은 과학시험에서 1점, 2번 학생은 2점과 같은 방식으로 점수를 얻었다고 생각해 보세요. 그래서 99번 학생은 99점, 100번 학생은 100점이 되는 것이죠.

또 편의상 각 반의 평균을 $\bar x_1$ , $\bar x_2$ , $\bar x_3$ , $\bar x_4$ , $\bar x_5$ 이고, 이 평균 값들의 평균을 $\bar x_c$ 라고 하겠습니다. 또한 전체 학생으로부터 구한 전체 평균을 $\bar x_T$ 로 표기하겠습니다.

이렇게 정하면 (2)식에서 구한 전체 학생의 평균인 50.5점이 $\bar x_T$ 가 되는 거에요.

2-1. 각 반의 학생수가 동일한 경우

아래의 [그림 1]은 학생수가 20명씩인 반이 5개가 있는데 각 반에서의 과학 성적 평균값들이 $\bar x_1$ , $\bar x_2$ , $\bar x_3$ , $\bar x_4$ , $\bar x_5$ 이에요.

[그림 1] 평균의 평균 식으로 구한 <span class="katex-eq" data-katex-display="false">\bar x_c</span>가 전체의 평균 <span class="katex-eq" data-katex-display="false">\bar x_T</span>와 같을까요? 이때 전체 학생 수는 총 100명이며, 각 반의 학생수는 모두 20명으로 동일합니다. — [그림 1] 평균의 평균 식으로 구한 $\bar x_c$ 가 전체의 평균 $\bar x_T$ 와 같을까요? 이때 전체 학생 수는 총 100명이며, 각 반의 학생수는 모두 20명으로 동일합니다.

이때 1반은 총 20명이 있어 1번부터 20번까지의 학생이 있고 1점부터 20점까지 점수가 분포해요. 2반은 21번부터 40번까지 21점부터 40점까지의 점수가 분포합니다. 또한 3반은 41번부터 60번까지 41점부터 60점까지 점수가 분포하며, 4반은 61번부터 80번까지 61점부터 80점까지 점수가 분포합니다. 마지막으로 5반은 81번부터 100번까지 81점부터 100점까지 점수가 분포한다고 생각하시면 됩니다.

1반부터 5반까지의 과학 성적 평균을 실제로 구해보면 다음과 같습니다.

\tag{3} \begin{align} \bar x_1 = 10.5\\ \bar x_2 = 30.5\\ \bar x_3 = 50.5\\ \bar x_4 = 70.5\\ \bar x_5 = 90.5 \end{align}

그러면 이제 이 평균값들의 평균을 구해보겠습니다.

\tag{4} \begin{align} \bar x_c &= {{\bar x_1 + \bar x_2 + \bar x_3 + \bar x_4 + \bar x_5}\over{5}}\\ &={{10.5 + 30.5 + 50.5 + 70.5 + 90.5}\over{5}}\\ &=50.5 \end{align}

각 반별 평균의 평균값이 50.5점이 나왔어요. 이 결과를 (2)식의 전체 평균값인 50.5와 비교했더니 놀랍게도 같다는 것을 알 수 있습니다.

그렇다면 반별 평균의 평균이 전체 평균과 같다는 결론이 얻어집니다.

그렇다면 다음의 경우와 같이 반별 학생수가 다르다면 어떻게 될까요?

2-2. 각 반의 학생수가 다른 경우

아래 [그림 2]는 위에서의 [그림 1]과 비슷합니다만, 각 반의 인원수가 서로 달라요. 다만 총 학생수는 100명으로 서로 동일합니다.

[그림 2] 각 반의 학생수가 서로 다른 경우 평균의 평균 식으로 구한 <span class="katex-eq" data-katex-display="false">\bar x_c</span>가 전체의 평균 <span class="katex-eq" data-katex-display="false">\bar x_T</span>와 같을까요? 이때 전체 학생 수는 총 100명입니다. — [그림 2] 각 반의 학생수가 서로 다른 경우 평균의 평균 식으로 구한 $\bar x_c$ 가 전체의 평균 $\bar x_T$ 와 같을까요? 이때 전체 학생 수는 총 100명입니다.

1반은 총 15명이 있어서 1번부터 15번까지의 학생이 있고 1점부터 15점까지 점수가 분포해요. 2반은 총 25명이 있어 16번부터 40번까지 16점부터 40점까지 점수가 분포해요. 3반은 총 20명이 있어 41번부터 60번까지 41점부터 60점까지 점수가 분포해요. 4반은 총 23명이 있는데 61번부터 83번까지 61점부터 83점까지 점수가 분포하며, 마지막 5반은 총 17명이 있는데 84번부터 100번까지 84점부터 100점까지 점수가 분포해 있어요.

1반부터 5반까지의 과학 성적 평균을 구하면 다음과 같습니다.

\tag{5} \begin{align} &\bar x_1 = 8.0\\ &\bar x_2 = 28.0\\ &\bar x_3 = 50.5\\ &\bar x_4 = 72.0\\ &\bar x_5 = 92.0 \end{align}

그러면 이제 이 평균값들의 평균을 구해보겠습니다.

\tag{6} \begin{align} \bar x_c &= {{\bar x_1 + \bar x_2 + \bar x_3 + \bar x_4 + \bar x_5}\over{5}}\\ &={{8.0 + 28.0 + 50.5 + 72.0 + 92.0}\over{5}}\\ &=50.1 \end{align}

각 반별 평균의 평균값이 50.1점이 나왔어요. 이 결과를 (2)식의 전체 평균값인 50.5와 비교했더니 서로 다르다는 것을 알 수 있습니다.

평균의 평균값인 50.1과 전체 평균인 50.5와는 분명히 다른 값이에요.

그래서 이번 글을 정리하면 다음과 같이 말할 수 있습니다. 각 반의 인원수가 서로 같으면 반별 평균의 평균값은 전체 평균과 같지만, 각 반의 인원수가 서로 다르면 반별 평균의 평균값은 전체 평균과 같지 않습니다.

그래서 실수나 오류를 줄이기 위해서는 되도록이면 전체 평균을 구할 때 부분 평균의 평균으로 구하는 것은 좋지 않을 것 같아요. 각 부분의 인원이 같다면 문제가 없으나 다르다면 평균값에 오류가 있게 됩니다.

3. 평균의 평균 값과 전체 평균 값이 일반적으로 다르다는 증명

학생들의 과학 점수를 $x_i$ 라고 했을 때 학생 100명의 전체 평균은 다음과 같습니다.

\tag{7} \bar x_T ={{x_1 + x_2 +\cdots+ x_{100}}\over{100}}

그런데 [그림 1]과 같이 각 반의 인원수가 20명으로 동일한 경우 각 반의 평균은 다음으로 구할 수 있어요.

\tag{8} \begin{align} &\bar x_1 = {{x_1 + x_2 + \cdots + x_{20} }\over{20}}\\ &\bar x_2 = {{x_{21} + x_{22}+\cdots+x_{40}}\over{20}}\\ &\bar x_3 = {{x_{41}+ x_{42}+\cdots+x_{60}}\over{20}}\\ &\bar x_4 = {{x_{61}+x_{62}+\cdots+x_{80}}\over{20}}\\ &\bar x_5 = {{x_{81}+x_{82}+\cdots+x_{100}}\over{20}} \end{align}

이 평균 값들의 평균을 구하면 다음과 같아요.

\tag{9} \begin{align} \bar x_c &= {{\bar x_1 + \bar x_2 + \bar x_3 + \bar x_4 + \bar x_5}\over{5}}\\ &={{{x_1 + x_2 + x_3 + \cdots+x_{98}+x_{99}+x_{100}}\over{20}}\over{5}}\\ &={{x_1 + x_2 + \cdots x_{100}}\over{100}} \end{align}

(9)식과 (7)식을 비교하면 서로 같아요. 즉 각 반의 인원수가 동일한 경우 평균의 평균은 전체 평균가 같습니다.

그러나 [그림 2]와 같이 반별 인원수가 서로 다른 경우는 어떻게 될까요? 반별 평균은 다음과 같이 계산됩니다.

\tag{10} \begin{align} &\bar x_1 = {{x_1 + x_2 + \cdots + x_{15} }\over{15}}\\ &\bar x_2 = {{x_{16} + x_{17}+\cdots+x_{40}}\over{25}}\\ &\bar x_3 = {{x_{41}+ x_{42}+\cdots+x_{60}}\over{20}}\\ &\bar x_4 = {{x_{61}+x_{62}+\cdots+x_{83}}\over{23}}\\ &\bar x_5 = {{x_{84}+x_{85}+\cdots+x_{100}}\over{15}} \end{align}

그렇다면 이 평균값들의 평균을 구한다면 (7)식과 같아질까요? 그렇지 않습니다. 왜냐하면 (10)식의 분모가 모두 다르기 때문이에요.

그래서 일반적인 경우 부분 집단 평균의 평균 값은 전체 평균 값과 같지 않게 됩니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 20 Average: 4.6]