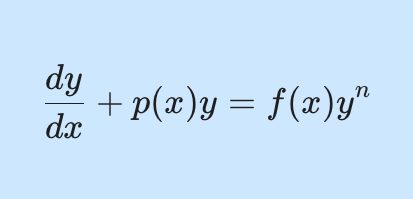Last Updated on 2025-01-29 by BallPen
1계 1차 비선형 미분방정식을 선형 미분방정식으로 변환하여 해를 구하는 방법을 알아 봐요.
1계 1차 비선형 미분방정식 중 일반해를 구하는 방법이 알려진 경우가 있어요. 대표적인 경우가 베르누이 미분 방정식(Bernulli differential equation)입니다.
베르누이 미분방정식의 해를 구하기 위해서는 비선형 미분방정식을 선형 미분방정식으로 변환한 후 풀면 되는데요.
이에 대해 상세히 알아 봐요. 아래는 이번 글의 목차입니다.
1. 1계 1차 선형 미분방정식 복습
1계 1차 선형 미분방정식의 표준 형태는 다음과 같아요.
\tag{1-1}
{{dy}\over{dx}} + p(x) y = r(x)그리고 윗 식에서 r(x)=0인 경우 제차형 1계 1차 선형 미분방정식, r(x) \ne 0인 경우 비제차형 1계 1차 선형 미분방정식이라고 합니다.
제차형 1계 1차 선형 미분방정식의 일반해는 다음과 같아요.
\tag{1-2}
y = c e^{-\int p(x)dx}그리고 비제차형 1계 1차 선형 미분방정식의 일반해는 다음 식과 같죠.
\tag{1-3}
y= e^{- \int p(x)dx} \Big[ \int e^{\int p(x) dx}r(x)dx + c \Big]2. 1계 1차 비선형 미분방정식 풀이 방법
1계 1차 비선형 미분방정식 중 베르누이 미분방정식은 일반해를 구하는 방법이 알려져 있어요. 베르누이 미분방정식의 기본 형태는 다음과 같아요.
\tag{2-1}
{{dy}\over{dx}} + p(x) y = f(x)y^n그리고 이 식이 비선형인 이유는 종속변수가 y^n으로 주어져 있기 때문이에요.
결국 1계 1차 선형 미분방정식과는 다른 형태이기 때문에 (1-2)식 또는 (1-3)식의 일반해 공식으로 해를 구할 수 없습니다.
하지만 (2-1)식을 약간 변형하면 선형 미분방정식으로 바꿀 수 있게 되는데요. 이에 대해 더 알아봐요.
2-1. 선형 미분방정식으로의 변환과 풀이
(2-1)식의 우변에 있는 y^n의 역수를 식의 양변에 곱해주면 다음과 같을 거에요.
\tag{2-2}
{1 \over y^n} {{dy}\over{dx}} + {1 \over y^n}p(x)y = f(x)그리고 윗 식을 더 정리하면 다음과 같죠.
\tag{2-3}
{1 \over y^n} {{dy}\over{dx}} + {1 \over y^{n-1}}p(x) = f(x)이제 치환을 할 건데요. 윗 식 중간에 있는 {1 \over y^{n-1}}을 u로 치환한 후 다음과 같이 양변을 독립변수 x에 대한 도함수를 구하면 다음과 같아요.
\begin{align*}
{1 \over {y^{n-1}}} = u
\end{align*}\begin{align*}
y^{1-n} =u
\end{align*}\begin{align*}
{d \over dx} y^{1-n} = {d \over dx} u
\end{align*}\begin{align*}
{d \over dy} y^{1-n} {{dy}\over{dx}} = {{du}\over{dx}}
\end{align*}\begin{align*}
(1-n)y^{-n} {dy \over dx} = {du \over dx}
\end{align*}\begin{align*}
{1 \over y^n} {dy \over dx} = {1 \over {1-n}} u^{\prime}
\end{align*}그런데 바로 윗 식의 좌변을 보면 (2-3)식의 가장 좌변항과 같은 모양이라는 것을 알 수 있어요. 그래서 (2-3)식에 바로 윗식을 대입하면 다음과 같습니다.
\tag{2-4}
{{u^{\prime}}\over{1-n}} + p(x)u = f(x)그리고 윗식을 다음과 같이 또 한번 정리할 수 있어요.
\tag{2-5}
u^{\prime} + (1-n) p(x) u = (1-n)f(x)윗 식을 조금 더 익숙한 형태로 바꾸면 다음과 같아요.
\tag{2-6}
{du \over dx} + (1-n) p(x) u = (1-n)f(x)이렇게 하고 났더니 윗 식을 잘 보시면 1계 1차 선형 미분방정식으로 변환되었음을 알 수 있어요. 즉 (1-1)식과 같은 형태가 되었다는 뜻이에요. 다만 y가 u로 바뀐 것만 달라요.
이제 (1-3)식으로 u에 대한 일반해를 구한 후 y로 바꾸어 정리하면 되는 거에요.
예제를 하나 풀어보겠습니다.
2-2. 예제
다음 (2-7)식에 미분방정식이 있어요. 이 미분방정식을 풀어 보세요.
\tag{2-7}
2xy{dy \over dx} + 2y^2 = 3x-6일단 윗 식을 정리해서 (2-1)식의 베르누이 미분방정식과 같은 형태가 되는지 알아봐요.
\tag{2-8}
{{dy}\over{dx}} + {{2y^2}\over{2xy}} = {{3x-6}\over{2xy}}\tag{2-9}
{{dy}\over{dx}} + {1 \over x} y = \Big({3 \over 2} - {{6}\over{2x}} \Big){1 \over y}그 결과 (2-9)식을 보면 (2-1)식의 베르누이 비선형 미분방정식과 형태가 같다는 것을 알 수 있어요. 이때 1/y는 y^{-1}로 보시면 됩니다.
이제 (2-9)식을 선형 미분방정식으로 바꾸면 되는데요. 일단 양변에 (2-9)식의 가장 오른쪽에 있는 y^{-1}의 역수인 y를 곱해주세요.
\tag{2-10}
y{{dy}\over{dx}} + {1 \over x} y^2 = \Big({3 \over 2} - {{6}\over{2x}} \Big)그리고 나중에 아래에서 필요해서 그런데요. 윗 식의 양변에 2를 곱해두도록 하겠습니다.
\tag{2-11}
2y{{dy}\over{dx}} + {2 \over x} y^2 = 2\Big({3 \over 2} - {{6}\over{2x}} \Big)그리고 윗 식 중간에 있는 y^2을 u로 치환하고 독립변수 x에 대한 도함수를 구하세요. 다음과 같이요.
\begin{align*}
y^2 =u
\end{align*}\begin{align*}
{d \over dx}y^2 = {d \over dx}u
\end{align*}\begin{align*}
{d \over dy} y^2 {dy \over dx} = {du \over dx}
\end{align*}\begin{align*}
2 y {dy \over dx} = {du \over dx}
\end{align*}그 결과 윗 식의 좌변을 보면 (2-11)식의 가장 좌변항과 그 형태가 같다는 것을 알 수 있어요. 그러므로 윗 식을 (2-11)식에 대입하고 정리하면 다음과 같이 되죠.
\tag{2-12}
{{du}\over{dx}} + {2 \over x} u= \Big({6 \over 2} - {{6}\over{x}} \Big)그 결과 윗 식은 (1-1)식 형태의 선형 미분방정식으로 바뀌었음을 알 수 있어요. 이제 (1-3)식을 적용해서 u를 구하면 됩니다.
\tag{2-13}
\begin{align}
u&=e^{- \int {{2}\over{x}} dx} \Big[\int e^{\int {2 \over x}dx} \Big({6 \over 2} - {6 \over x} \Big)dx+c\Big]\\[10pt]
&=e^{-2 \ln x} \Big[\int e^{2 \ln x} \Big({6 \over 2} - {6 \over x} \Big)dx + c \Big]\\[10pt]
&=x^{-2} \Big[ \int x^2 \Big({6 \over 2} - {6 \over x} \Big) dx + c \Big]\\[10pt]
&=x^{-2} \Big[\int 3x^2 dx - \int 6xdx + c \Big]\\[10pt]
&=x^{-2} (x^3 - 3x^2 + c)\\[10pt]
&=x - 3 + x^{-2}c
\end{align}이때 y^2=u이므로 y^2은 다음과 같아요.
\tag{2-14}
y^2 = x-3 + x^{-2}c바로 윗 식의 y가 (2-7)식에 주어진 1계 1차 비선형 미분방정식의 일반해입니다.