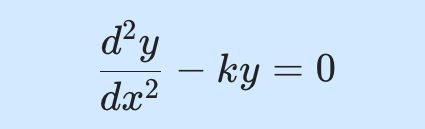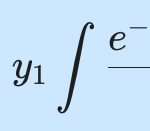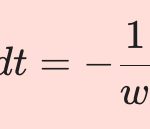Last Updated on 2024-12-05 by BallPen
제차 2계 상미분 방정식 예제를 하나 풀어보겠습니다.
2계 상미분 방정식 문제 하나를 풀어봐요. 과학과 공학분야에서 간혹 나타나는 형태의 방정식인데요.
아래의 미분방정식입니다. 이 식에서 k는 임의의 상수에요.
\begin{align*}
{{d^2 y}\over{dx^2}} - ky=0
\end{align*}이 식의 일반해를 구하면 다음과 같이 주어집니다. 물론 D와 E도 임의의 상수에요.
\begin{align*}
y(x) = D e^{kx} + E e^{-kx}
\end{align*}이제부터 어떻게 일반해를 구했는지 구체적으로 알아봐요. 참고로 구체적인 상수계수를 갖는 제차 2계 상미분 방정식의 일반적 풀이 방법은 링크된 다른 글을 참고하시기 바랍니다.
아래는 이번 글의 목차입니다.
Contents
1. 제차 2계 상미분 방정식
제차 2계 상미분방정식의 일반형은 다음과 같습니다.
\tag{1}
{{d^2 y}\over{dx^2}} + p(x){{dy}\over{dx}} + Q(x)y =0일반형을 라그랑주(Joseph-Louis Lagrange, 1736-1813) 미분기호를 사용하면 y^{\prime \prime} + p(x) y^{\prime} + Q(x) y =0 으로 표기하기도 해요.
그런데 만약 (1)식을 만족하는 해 하나를 알고 있다고 생각해봐요. 그리고 그 해를 y_1 (x)라고 할께요. 그러면 두번째 해 y_2 (x)는 어떻게 구할 수 있을 까요?
바로 계수 낮추기(reduction of order) 법으로 유도되는 아래의 공식을 활용하면 구할 수 있습니다.
\tag{2}
\begin{align}
y_2 (x) = y_1 \int {{e^{-\int pdx}}\over{{y_1}^2}} dx
\end{align}이렇게 구한 두번째 해 y_2(x)와 이미 알고 있는 첫번째 해 y_1(x)는 중첩과 선형성의 원리에 따라 다음과 같이 표기할 수 있어요. 이 식이 바로 일반해입니다.
\tag{3}
\begin{align}
y(x) = c_1 y_1 (x) + c_2 y_2 (x)
\end{align}윗식에서 c_1과 c_2는 임의의 상수에요.
2. 예제
자연과학이나 공학 공부를 하다보면 간혹 아래 형태의 미분방정식을 만나는 경우가 있어요. 이 미분방정식의 일반해를 구해보기로 해요.
\tag{4}
\begin{align}
{{d^2 y}\over{dx^2}} - kx =0
\end{align}(4)식을 만족하는 일반해 하나를 추정해보기 위해 일단 다음과 같이 표현해봐요.
\tag{5}
\begin{align}
{{d^2 y}\over{dx^2}} = kx
\end{align}그러면 윗 식을 만족하는 해는 지수함수일 것을 짐작할 수 있어요. 왜냐면 어떤 함수 y를 x로 두번 미분했을 때 y를 k배한 결과가 나오기 때문이에요.
즉, (4)식을 만족하는 해 중 하나는 다음의 형태가 되어야 합니다.
\tag{6}
y_1 (x) = A e^{kx}여기서 물론 A는 임의의 상수에요.
첫번째 해를 구했으니 이번에는 두번째 해를 구해 봐요. 이를 위해서는 (2)식을 이용하면 되는데요.
이를 위해 우선 (4)식을 (1)식의 일반형과 비교해 보면 p(x)=0이 됨을 알 수 있어요. 따라서 (2)식을 적용하면 두번째 해는 다음과 같아요.
\tag{7}
\begin{align}
y_2 (x) &= y_1 \int {{e^{-\int pdx}}\over{{y_1}^2}} dx\\[10pt]
&=Ae^{kx} \int {{e^{-\int 0 dx}}\over{(Ae^{kx})^2}} dx \\[10pt]
&=Ae^{kx} \int {{e^{0}}\over{(Ae^{kx})^2}} dx \\[10pt]
&= Ae^{kx} \int {{1}\over{(Ae^{kx})^2}} dx \\[10pt]
&=Ae^{kx} \int {1 \over {A^2}} e^{-2kx}dx\\[10pt]
&={{e^{kx}} \over {A}} \Big(-{1 \over {2k}} e^{-2kx} + C \Big)\\[10pt]
&=-{{1}\over{2kA}} e^{-kx} + {C \over A} e^{kx}
\end{align}그러면 (6)식과 (7)식의 두 해를 결합하면 다음과 같이 일반해를 구할 수 있어요.
\tag{8}
\begin{align}
y(x) &= y_1 (x) + y_2 (x)\\[10pt]
&= Ae^{kx} - {1 \over {2kA}} e^{-kx} + {C \over A} e^{kx}\\[10pt]
&=De^{kx} + E e^{-kx}
\end{align}윗 식에서 상수들은 D와 E로 치환해서 표현했어요. 만일 특수해를 구하고 싶다면 초기조건을 적용해야 합니다.
지금까지 2계 상미분 방정식 예제를 풀어보았습니다.