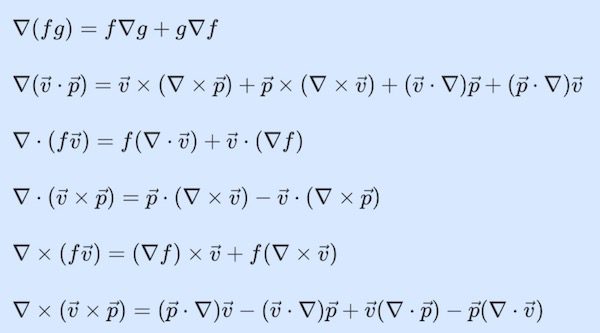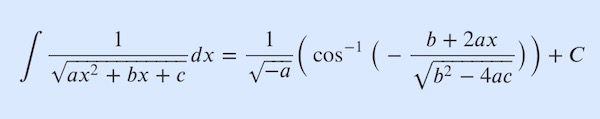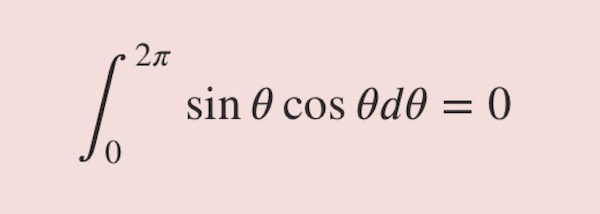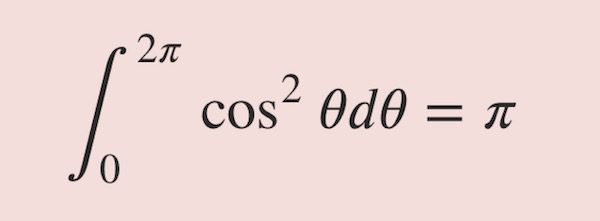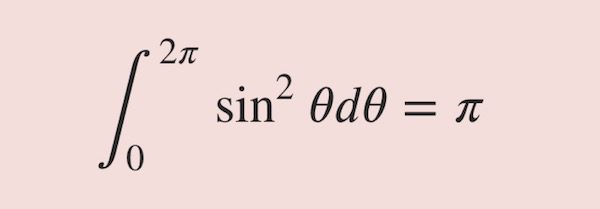변분(variation)5 (1)
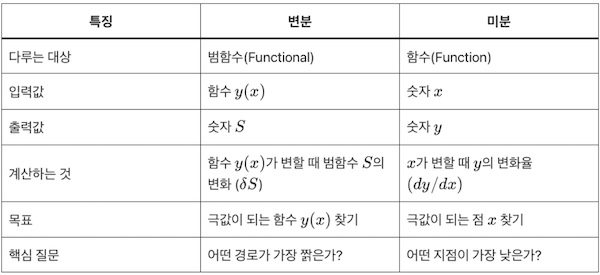
변분의 개념을 알아보고 미분과의 차이점을 이해해 봐요. 변분(variation)이란 함수의 모양이 아주 조금씩 변할 때(), 출력값()가 얼마나 변하는지()를 계산하는 것을 말합니다. 반면에 미분이란 입력값()이 아주 조금씩 변할 때, 출력값()이 얼마나 변하는지를 계산해요. 이 글에서는 미분과 비교하여 변분에 대한 주요 개념을 알아 보겠습니다. Contents1. 미분(differentiation)2. 변분 (Variation)3. 변분 vs. 미분3-1. 개념 비교3-2. 연산규칙 비교 1. 미분(differentiation) 미분에서 … Read more