Q 인자(Quality Factor)

Last Updated on 2025-08-08 by BallPen

한번 흔들어진 진동자가 얼마나 오랫동안 진동을 유지할 수 있는가의 척도인 Q 인자에 대해 알아 봐요.

Q 인자(quality factor)는 Q 인수, Q 값이라고도 불리는데요. 이 인자는 진동을 시작한 진동자가 얼마나 오랬동안 그 진동을 유지할 수 있는가의 척도입니다.

예를 들어, 공기 중 용수철에 매달린 물체를 당겼다가 놓으면 진동을 시작하는데요. 당연히 오랫동안 그대로 두면 공기저항력에 의해 진동이 멈추게 됩니다.

그런데 이 과정에서 어떤 진동자는 금방 멈춰버리기도 하고 어떤 진동자는 꽤 오랫동안 진동을 유지하기도 해요.

이와 같이 진동자가 얼마나 오랫동안 진동을 유지할 수 있는지의 평가 척도가 바로 Q 인자에요. Q 인자가 클수록 진동을 유지하는 시간이 길어져요.

Q 인자는 다음 식으로 정의됩니다.

\begin{align}
Q = {{E}\over{\Delta E}}\times 2 \pi
\end{align}

여기서 \(E\)는 어느 시간 \(t\)에서 진동자가 갖는 총 에너지이고, \(\Delta E\)는 한 주기 동안 진동자가 잃어 버리는 에너지입니다.

이제 부터 위 식이 어떤 의미를 갖는지, 그리고 실제 진동자에서 위 정의식이 어떻게 표현되는지 알아 보겠습니다.

1. 미흡감쇠 진동자의 Q 인자

예로써, 미흡감쇠 진동자에 대한 Q 인자를 구해보도록 해요. 이를 구하기 위해서는 먼저 미흡감쇠 진동자의 에너지 손실율을 구해야 해요.

1-1. 미흡감쇠 진동자의 에너지 손실율

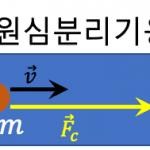
아래 [그림 1]은 용수철 상수 \(k\)인 용수철에 질량 \(m\)인 물체가 매달려 감쇠조화진동하는 모습을 나타내고 있어요.

물체가 속도 \(v\)로 아래 방향으로 움직이는 상황이고요.

진동중심보다 아래쪽에 물체가 있으므로 복원력 \(-kx\)는 위쪽을 향합니다. 그리고 공기저항력은 속도의 반대방향으로 작용하므로 위쪽 방향으로 \(-cv\)가 작용해요.

결국 물체의 운동방정식은 다음과 같아요.

\begin{align}
\tag{1-1}
\sum F = {\color{blue}{-kx – cv = ma}}
\end{align}

그러므로 윗 식 파랑색 부분을 도함수를 이용해 다시 표현하면 다음과 같아요.

\begin{align}
\tag{1-2}
m{{d^2x}\over{dt^2}} + c{{dx}\over{dt}} +kx =0
\end{align}

한편 용수철 진동자가 갖는 역학적 에너지는 다음 식으로 주어집니다.

\begin{align}
\tag{1-3}
E = {1 \over 2} m \Big({{dx}\over{dt}}\Big)^2 + {1 \over 2} kx^2
\end{align}

그리고 위 역학적 에너지를 시간으로 미분해보도록 해요. 그러면 미흡감쇠 진동자의 에너지 감소율을 구할 수 있어요.

\begin{align}
\tag{1-4}
\require{cancel}
{{dE}\over{dt}} &= {1 \over {\cancel 2}} m \Big( {\cancel 2} {{dx}\over{dt}}{{d^2 x}\over{dt^2}}
\Big) + {1 \over {\cancel 2}} k\Big( {\cancel 2}x{{dx}\over{dt}}\Big)\\[8pt]
&=m{{dx}\over{dt}} {{d^2 x}\over{dt^2}} + kx{{dx}\over{dt}}\\[8pt]
&=\Big({\color{red}{m{{d^2x}\over{dt^2}} + kx}} \Big) {{dx}\over{dt}}\\[8pt]
&=\Big( {\color{red}{- c {{dx}\over{dt}}}}\Big){{dx}\over{dt}}\\[8pt]
&=-c \Big({{dx}\over{dt}}\Big)^2\\[8pt]
&= -cv^2
\end{align}

위 식에서 빨강색 부분은 (1-2)식을 반영한 거에요. 결과를 보면 음수가 나오는데요. 이 것은 시간에 따라 역학적 에너지가 점점 감소함을 뜻해요. 이 에너지 감소 때문에 진동은 영원히 진동하지 못하고 결국 멈추게 되는 것이죠.

만일 감쇠계수 \(c=0\)이 되어 감쇠력 없다면 (1-4) 식은 0이 됩니다. 이 뜻은 총 역학적 에너지 \(E\)가 상수임을 의미하고 진동이 영원히 유지됨을 뜻해요.

1-2. 미흡감쇠 진동자가 한 주기 동안 잃는 에너지

미흡감쇠 진동자가 한 주기 동안 잃는 에너지를 구하기 전에 먼저 미흡감쇠 진동의 속도 \(v\)를 구해보도록 해요. 이 \(v\)는 (1-4)식의 마지막 줄에 있는 \(v\)와 같아요. 이것을 먼저 구해놔야 나중에 편리하게 사용하게 되거든요.

[미흡감쇠 진동자의 속도]

미흡감쇠 진동자의 변위 \(x(t)\)는 다음과 같아요.

\begin{align}
\tag{1-5}
x(t) = Ae^{-\gamma t} (\sin (\omega_{d}t + \phi_0)
\end{align}

여기서 \(\gamma\)는 감쇠인자로 \(c/2m\)의 관계가 있습니다. 위 식을 시간으로 미분하면 속도 \(v(t)\)를 구할 수 있어요. 그 결과는 아래와 같습니다.

\begin{align}
\tag{1-6}
v(t) = {{dx}\over{dt}} &= -A \gamma e^{-\gamma t} \sin(\omega_{d}t + Ae^{-\gamma t} \omega_d \cos (\omega_d) t + \phi_0)\\
&=-A e^{-\gamma t} \big[\gamma \sin (\omega_d t + \phi_0) – \omega_d \cos (\omega_d t + \phi_0)\big]
\end{align}

이때 위 (1-6)식에서 \(\omega_d t + \phi_0 =\theta\)로 치환하도록 해요. 그러면 아래 조건이 성립하고, \(t\)를 0에서 한주기 \(T_d\)까지 변화시킬 때 \(\theta\)는 0에서 \(2\phi\)까지 변화됨을 알 수 있어요.

\begin{align}
\tag{1-7}
\require{cancel}
&{{d\theta}\over{dt}} = \omega_d\\
&t=0 \rightarrow \theta = \phi_0 = 0\\
&t=T_d \rightarrow \theta = \omega_d T_d = {\cancel{\omega_d}} \Big({{2 \phi}\over{{\cancel{\omega_d}}}}\Big)=2 \phi
\end{align}

윗 식에서 편의상 초기위상은 \(\phi_0 = 0\)으로 간주했어요.

[한 주기 동안 잃는 에너지]

한 주기 동안 미흡감쇠 진동자가 잃어버리는 에너지 \(\Delta E\)를 구하기 위해서는 (1-4)식을 활용합니다. (1-4)식을 \(d E\)에 대해 정리하면 다음과 같아요.

\begin{align}
\tag{1-8}
dE = -cv^2 dt
\end{align}

위 식에서 \(t\)가 \(0\)에서 한 주기 \( T_d \)까지 변하는 동안 에너지가 \(E_0\)에서 \(E\)까지 \(\Delta E\)만큼 감소한다고 생각해봐요. 그러면 한 주기 동안 감소된 에너지 \(\Delta E\)는 (1-8)식의 양변을 다음과 같이 적분하면 됩니다.

\begin{align}
\tag{1-9}
\Delta E = \int_{E_0}^E dE = \int_0^{T_d} -cv^2 dt
\end{align}

그리고 위 식의 \(v\)에 (1-6)식을 대입하고 (1-7)식의 조건을 적용해 봐요. 그러면 다음과 같습니다.

\begin{align}
\tag{1-10}
\Delta E &= \int_0^{T_d} -cv^2 dt\\
&=\int_0^{2\pi} -cv^2 \Big({{d\theta}\over{\omega_d}}\Big)\\
&=-{{c}\over{\omega_d}} \int_0^{2\pi} v^2 d\theta\\
&=-{{c}\over{\omega_d}}A^2 e^{-2 \gamma t} \int_0^{2\pi} \big( \gamma^2 {\color{red}{\sin^2 \theta}} + \omega_d^2 {\color{red}{\cos^2 \theta}} – 2 \gamma \omega_d {\color{red} {\sin \theta \cos \theta}} \big) d \theta
\end{align}

이때 윗 식에서 \(\sin^2 \theta\)의 한 주기 적분과 \(\cos^2\theta\)의 한 주기 적분은 각각 \(\pi\)이고, \(\sin \theta \cos \theta\)의 한 주기 적분은 0이 됩니다.

이 결과를 반영하면 위 (1-10)식은 다음과 같아요.

\begin{align}
\tag{1-11}
\Delta E = – {{c}\over{\omega_d}} A^2 e^{-2 \gamma t} \pi (\gamma^2 + \omega_d^2)
\end{align}

한편 미흡감쇠진동자의 각진동수 \(\omega_d\)와 공명진동수 \(\omega_0\)사이에는 \(\omega_d = \sqrt{\omega_0^2 – \gamma^2} \)의 관계가 성립합니다. 따라서 (1-11)식은 다음과 같아요. 여기서 \(c=2m\gamma\)의 관계를 적용하였고, 분자와 분모에 2를 곱하고 나누어 식을 변형했어요.

\begin{align}
\tag{1-12}
\require{cancel}
\Delta E &= – {{c}\over{\omega_d}} A^2 e^{-2 \gamma t} \pi \omega_0^2\\
&=-{\cancel 2}m \gamma A^2 e^{-2 \gamma t} \Big({{\omega_0^2}\over{\color{red}{\cancel 2}}}\Big) \Big({{{\color{red}2} \pi}\over{\omega_d}}\Big)\\
&=-m\gamma A^2 e^{-2 \gamma t} \omega_0^2 T_d\\
&={1 \over 2} m\omega_0^2 A^2 \big( -2 \gamma e^{-2 \gamma t} \big) T_d
\end{align}

윗 식에서 특성시간 \(\tau\)를 \(\tau = {1/2\gamma}\)로 정의하면, \(\gamma ={1/2 \tau}\)이 성립합니다. 이를 반영하면 다음과 같아요.

\begin{align}
\tag{1-13}
\Delta E = {1 \over 2} m\omega_0^2 A^2 \big( -2 {1 \over {2 \tau}} \big)e^{-{t \over \tau}}T_d
\end{align}

결국 미흡감쇠진동자가 한주기 동안 잃어버리는 에너지 \(\Delta E\)는 다음과 같아요.

\begin{align}
\tag{1-14}
\Delta E = \color{blue}{{1 \over 2} m\omega_0^2 A^2 e^{-{t \over \tau}}}{{T_d}\over{\tau}}
\end{align}

1-3. 미흡 감쇠 진동자의 Q 인자

위 (1-14)식에서 파랑색 수식은 시간 \(t\)에 대해 지수적으로 감소하는 파동에너지 \(E\)를 의미합니다. 양변을 \(E\)로 나누면 다음과 같습니다.

\begin{align}
\tag{1-15}
{{\Delta E}\over{E}} = {{T_d}\over{\tau}}
\end{align}

마지막으로 위 식의 역수를 취한 후 양변에 \(2\pi\)를 곱해주면 미흡감죄 진동자의 \(Q\) 인자 정의식이 도출됩니다.

\begin{align}
\tag{1-16}
Q = {{E}\over{\Delta E}} \times 2\pi = {{\tau}\over{T_d}}\times 2\pi
\end{align}

그런데 여기서 \(2\pi\)를 왜 곱하는지 궁금할 텐데요. 그 이유는 주기 \(T_d = {{2\pi}\over{\omega_d}}\)의 관계식을 대입했을 때 \(2\pi\)가 서로 약분되도록 하기 위함이에요.

\begin{align}
\tag{1-17}
\require{cancel}
Q = {{E}\over{\Delta E}} \times 2\pi &= {{\tau}\over{T_d}}\times 2\pi\\[5pt]
&={{\tau}\over{\cancel {2\pi/}\omega_d}} \times \cancel{2\pi}\\[5pt]
&=\omega_d \tau\\[5pt]
&={{\omega_d}\over{2 \gamma}}
\end{align}

윗 식이 미흡감쇠진동자의 Q 인자 입니다.

2. 진동수 응답 특성으로부터 Q 인자 구하기

Q 인자를 구한다는 것은 감쇠가 아주 약한 진동자를 고려하고 있다는 의미에요. 감쇠가 큰 경우에는 Q 인자를 굳이 고민하지 않겠죠.

또한 (1-17)식을 통해서도 Q 인자를 구할 수 있겠지만, 실용적인 측면에서 진동의 진동수 응답특성으로부터 Q 인자를 구해야 하는 경우가 있을 수 있어요. 이럴 때는 어떻게 구할 수 있을까요?

이에 대한 이야기를 더 진행해 보겠습니다.

2-1. 감쇠가 아주 작은 경우 강제감쇠진동자의 진동진폭

우선 감쇠가 아주 약한 경우를 다루고 있으므로 몇가지 가정을 세우도록 해요.

감쇠인자 \(\gamma\)가 무척 작아 다음의 관계가 성립한다고 가정할게요.

\begin{align}
\tag{2-1}
&\gamma << \omega_0\\[5pt]
&\gamma^2 \approx 0\\[5pt]
& A_{max} = {{F_0 / m}\over{2 \gamma \omega_0}}\\[5pt]
& \omega_0^2 – \omega^2 = (\omega_0 + \omega) (\omega_0 – \omega) \approx 2 \omega_0 (\omega_0 – \omega)\\[5pt]
&\gamma \omega \approx \gamma \omega_0
\end{align}

위에서 \(A_{max}\)는 진동수응답특성에서 최대 진동 진폭을 의미합니다. 이 식의 도출 과정에 대해서는 다른 글을 통해 따로 설명드릴게요. 일단 위 식이 성립한다고 받아들이고 시작하시기 바랍니다.

강제감쇠진동자의 진동진폭은 다음 식으로 주어집니다.

\begin{align}
\tag{2-2}
\require{cancel}
A(\omega) &= {{F_0/m}\over{\sqrt{(\omega_0^2 – \omega^2)^2 + (2 \gamma \omega)^2}}}\\
&\approx = {{F_0/m}\over{\sqrt{4 \omega_0^2 (\omega_0 – \omega)^2 + 4 \gamma^2 \omega_0^2}}}\\
&={{F_0/m}\over{2 \omega_0 \sqrt{(\omega_0 – \omega)^2 + \gamma^2}}}\\
&={{A_{max}({\cancel 2} \gamma {\cancel \omega_0)}}]\over{\cancel {2 \omega_0} \sqrt{(\omega_0 – \omega)^2 + \gamma^2}}}\\
&={{A_{max} \gamma}\over{\sqrt{(\omega_0 – \omega)^2 + \gamma^2}}}
\end{align}

한편 \(|\omega_0 – \omega|=\gamma\)인 두 지점을 생각해봐요. 그러면 \(\omega = \omega_0 \pm \gamma\)인 곳에서의 진폭은 다음과 같아요. 즉, \(\omega = \omega_0 \pm \gamma\)를 위 (2-2)식의 가장 마지막 줄에 대입하면 다음 관계가 성립합니다.

\begin{align}
\tag{2-3}
A(\omega_0 \pm \gamma) &= {{A_{max} \gamma}\over{\sqrt{\gamma^2 + \gamma^2}}}\\
&={{A_{max}\gamma}\over{\sqrt{2} \gamma}}\\
&={{A_{max}}\over{\sqrt{2}}}
\end{align}

2-2. 진동수응답특성에서 구하는 Q 인자

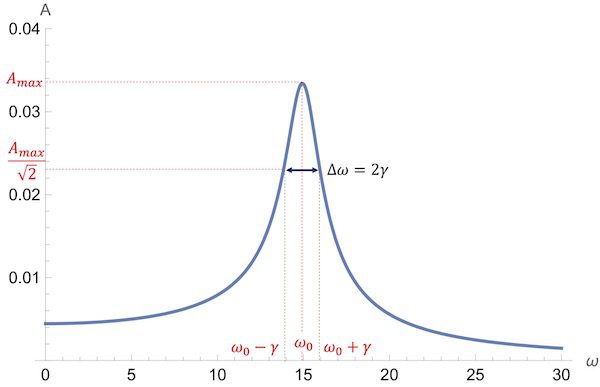
아래 [그림 2]는 강제감쇠진동자의 진동수응답특성 곡선이에요.

\(y\)축이 진동의 진폭 \(A\)일 때 (2-3)식에서와 같이 \({{A_{max}}\over{\sqrt{2}}}\)는 \(\omega = \omega_0 \pm \gamma\)지점에서의 높이에 해당합니다.

따라서 이 높이에서의 진동수응답특성 곡선의 폭 \(\Delta \omega\)는 [그림 2]와 같이 \(2\gamma\)와 같습니다.

그런데 미흡감쇠진동자에 대한 Q인자인 (1-17)식에서 감쇠인자가 매우 작다면 다음의 관계가 성립합니다.

\begin{align}
\tag{2-4}
Q &= {{\omega_d}\over{2 \gamma}}\\[5pt]
&\approx {{\omega_0}\over{2 \gamma}}
\end{align}

그리고 윗 식의 분모인 \(2\gamma\)는 \({{A_{max}}\over{\sqrt{2}}}\)높이에서 곡선의 폭 \(\Delta \omega\)와 같으므로 아래의 관계식이 성립합니다.

\begin{align}
\tag{2-5}
Q \approx {{\omega_0}\over{2 \gamma}}={{\omega_0}\over{\Delta \omega}}
\end{align}

결국 진동수 응답특성에서 \(\omega_0\)와 \(\Delta \omega\)를 측정하면 Q 인자를 구할 수 있게 되는 거에요.

만일 진동수 응답 특성의 \(y\)축이 진폭의 제곱인 \(A^2\)으로 그려져 에너지의 척도를 갖는다면, 그 경우 \(2\gamma\)는 \({{A_{max}^2}\over{2}}\)높이가 \(\Delta \omega\)에 해당한다는 것을 기억하시기 바랍니다.

이때의 \(\Delta \omega\)를 반치전폭(FWHM, full width at half maximum)이라 부릅니다.

3. 직렬 RLC 회로에서의 공명과 Q 인자

직렬 RLC 회로에서의 공명현상도 감쇠진동자와 동일한 역학 관계를 갖습니다. 이 두 현상 사이의 대응관계는 다음과 같아요.

기호	감쇠진동자	기호	RLC회로
\(x\)	변위	\(q\)	전하량
\(v\)	속도	\(i\)	전류
\(m\)	질량	\(L\)	인덕턴스
\(k\)	용수철상수	\(1/C\)	전기용량의 역수
\(c\)	감쇠계수	\(R\)	저항
\(F\)	힘	\(V\)	전위차

위 표에 주어진 관계를 적용하면 직렬 RLC 회로에서의 Q 인자를 정의할 수 있습니다. 이를 위해 우선 (2-5)식을 조금 변형하면 다음과 같다는 것을 알 수 있어요.

\begin{align}
\tag{3-1}
Q &\approx {{\omega_0}\over{2 \gamma}}\\[5pt]
&={{\omega_0}\over{2 (c/2m)}}\\[5pt]
&={{\omega_0 m}\over{c}}
\end{align}

그리고 표에서의 대응관계를 적용하면 다음과 같습니다.

\begin{align}
\tag{3-2}
Q \approx {{\omega_0 L}\over{R}}
\end{align}

바로 윗 식이 직렬 RLC 공명회로에서의 Q 인자 입니다.