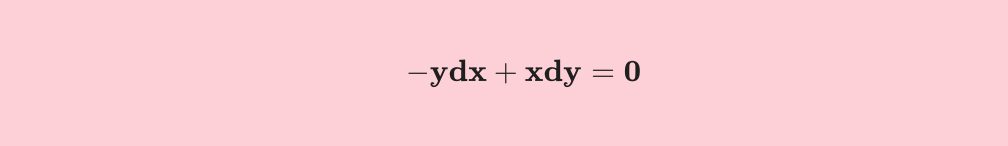Last Updated on 2025-09-09 by BallPen
주어진 미분방정식을 풀어 보세요.
아래의 미분방정식을 풀어보세요.
\tag{1}
\bold{-ydx + xdy =0}이 미분방정식은 두개의 풀이법을 적용할 수 있어요. 하나는 변수분리형 미분방정식 풀이법을 적용할 수 있고, 다른 하나는 불완전미분방정식 풀이법을 적용할 수 있습니다.
아래는 이번 글의 목차입니다.
1. 변수분리형 미분방정식 풀이법 적용
주어진 문제의 변수를 x와 y로 분리해 보세요. 그러면 아래와 같습니다.
\tag{2}
\begin{align}
ydx &= xdy\\
\end{align}\tag{3}
{1 \over x} dx = {1 \over y} dy
(3)식의 양변을 적분해보세요.
\tag{4}
\ln x+\ln c_1 = \ln y + \ln c_2 (4)식에서 c_1과 c_2는 상수입니다. 이 식을 더욱 정리해봐요. 그리고 로그의 성질을 활용하면 아래 (5)식과 같이 표현할 수 있습니다.
\tag{5}
\begin{aligned}
&\ln x = \ln y + (\ln c_2 - \ln c_1)\\[10pt]
&\ln x = \ln y + \ln c\\[10pt]
&\ln x = \ln (cy)
\end{aligned}여기서도 c는 상수입니다. 마지막으로 (5)식을 다시 한번 더 정리하면 다음의 일반해가 도출됩니다.
\tag{6}
x=cy2. 불완전미분방정식 풀이법 적용
2-1. 적분인자 구하기
(1)식에 주어진 미분방정식은 불완전미분방정식입니다. 이때 적분인자 1/x^2를 양변에 곱해주면 완전미분방정식이 돼요.
이때 적분인자를 어떻게 구하는지는 불완전미분방정식 풀이법에 대한 글을 참고하기 바랍니다.
적분인자를 (1)식의 양변에 곱하면 아래의 식이 됩니다.
\tag{7}
-\Big({1 \over x^2}\Big )ydx + \Big({1 \over x^2}\Big)xdy = \Big({1 \over x^2}\Big)0
\tag{8}
-{y \over x^2}dx + {1 \over x}dy =02-2. 완전미분방정식 풀이법 적용
이제 (8)식에 완전미분방정식 풀이법을 순서대로 적용하면 됩니다.
우선 아래의 관계가 성립함을 우리는 알고 있습니다.
\tag{9}
{\partial f(x,y) \over \partial x} = -{y \over x^2}(9)식을 정리하면 아래의 관계가 성립합니다.
\tag{10}
df(x,y) = - {y \over x^2} dx(10)식의 양변을 적분해서 f(x,y)=c_1을 구합니다.
\tag{11}
\begin{align}
\int df(x,y) = -\int {y \over x^2} dx\\
\end{align}\tag{12}
f(x,y) = {y \over x} + k(y) = c_1
(12)식에서 k(y)는 y만의 함수를 뜻합니다.
이번에는 아래 (13)식의 관계를 이용해요.
\tag{13}
{\partial f(x,y) \over \partial y} = {1 \over x}(12)식의 f(x,y)를 (13)식에 대입하면 아래와 같이 됩니다.
\tag{14}
\begin{aligned}
{\partial \over \partial y}\Big( {{y \over x} + k(y)\Big)} = {1 \over x}\\[10pt]
\cancel{1 \over x} + {{dk(y) \over {dy}}} = \cancel{1 \over x}\\[10pt]
{{dk(y)\over d y}} = 0
\end{aligned}(14)식의 마지막 줄이 성립하기 위해서는 k(y)는 상수가 되어야 합니다.
\tag{15}
k(y) = c_2이제 마지막 절차로서 (15)식의 k(y)를 (12)식에 대입하고 정리합니다.
\tag{16}
\begin{aligned}
f(x,y) = &{y \over x} + k(y) = c_1\\[10pt]
&{y \over x} + c_2 = c_1\\[10pt]
&{y \over x} = (c_1 - c_2)\\[10pt]
&{y \over x} = c_3
\end{aligned}
(16)식의 마지막줄을 최종적으로 다시 한번 더 정리해 봅니다.
\tag{17}
x = {y \over c_3} =cy불완전미분방정식 풀이법으로 구한 (17)식의 일반해는 변수분리형 미분방정식 풀이법으로 구한 (6)식의 해와 동일합니다.