소음도 가산과 감산 연습 문제

Last Updated on 2023-05-01 by BallPen

두 개 이상의 소음원이 있을때 소음도(음압레벨)는 어떻게 합산할 수 있을까요? 그리고 측정한 소음도에서 배경음을 제외하고 싶다면 어떻게 감산해야 할까요?

소음도 (SPL, Sound Pressure Level)란 소음 원천에서 생성되는 압력진폭(pressure amplitude) 또는 소리의 세기(intensity)를 이용하여 데시벨 (dB) 단위로 표기하는 소음의 정도를 말합니다.

소음도, 음압레벨, 등가소음도 등에 대해 궁금한 사람은 이곳으로 이동하면 자세히 알 수 있어요.

그런데 소음도를 계산 할 때 간혹 어느 소음원으로부터 방출된 소음도와 다른 소음원으로부터 방출된 소음도을 서로 합해야 하는 경우가 있습니다.

반대로 이미 얻어진 전체 소음도로부터 특정 소음도를 제외하는 감산을 해야 하는 경우도 있어요.

이때 dB 단위를 갖는 소음도를 단순하게 합하거나 빼면 안되는데요. 이에 대해 알아보고 연습문제를 풀어보겠습니다.

목차는 다음과 같습니다.

1. 소음도 가산과 감산의 잘못된 사례

1-1. 가산의 잘못된 사례

예를 들어 아래 그림처럼 두개의 소음원인 기계 A와 기계 B로부터 방출된 소음도를 각각 L_{a1}, ~L_{a2}라고 하겠습니다. 이 두 소음도가 합해진 소음도는 얼마가 될까요?

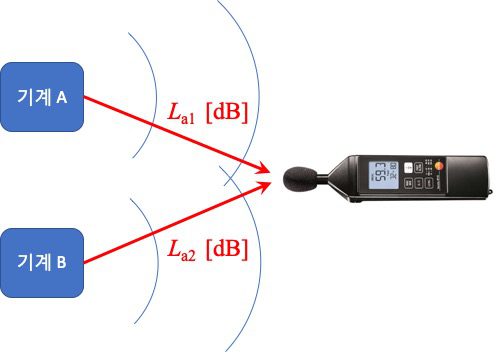
만일 L_{a1} = 70~\mathrm{dB}이고 L_{a2} = 72~\mathrm{dB}이라고 하면 전체 소음도는 각각의 소음도를 합하여 142 dB이 될까요?

아니오 그렇지 않습니다. 소음도의 덧셈을 이렇게 계산하면 틀립니다.

1-2. 감산의 잘못된 사례

이번에는 전체 소음도 L_t에서 La_1이라는 소음도를 빼낸다면 결과 소음도는 어떻게 될까요?

예를 들어 위 그림에서 소음계로 측정한 전체 소음도 L_t에서 L_{a1}을 빼어 L_{a2}를 구하는 상황으로 보시면 쉽습니다.

만일 전체소음도가 L_t =62~\mathrm{dB}인데 L_{a1} = 60~\mathrm{dB}을 빼낸다면 결과 소음도는 두 소음도의 차이인 2 dB이 될까요?

이번에도 틀렸습니다. 소음도의 뺄셈을 이렇게 계산하면 틀립니다.

2. 소음도 가산과 감산 공식의 유도

2-1. 가산 공식

소음도, 즉 음압 레벨은 아래의 공식으로 표현됩니다.

\tag{1}
L_a = 10 \log \Big({{p}^2\over{p_0}^2} \Big)

여기서 p는 소음원에서 발생하는 압력 진폭의 실효값이고, p_0는 기준 압력 진폭의 실효값으로 20~ \mu \mathrm{Pa}에 해당합니다.

소음도가 가산된다는 것은 바로 (1)식에서 {p^2 / {p_0}^2}이 가산된다는 것을 뜻합니다. 절대로 dB 단위를 단순히 합하시면 안됩니다.

예를 들어 소음원이 3개가 있고 각각의 소음도를 L_{a1} ,~L_{a2} ,~L_{a3}라고 하겠습니다. 그리고 각 소음원에서 발생되는 압력진폭을 p_1 ,~p_2 ,~p_3로 가정하겠습니다.

그러면 이러한 압력진폭이 합해졌을 때 전체 소음도 공식은 아래 (2)식과 같이 표현할 수 있습니다.

\tag{2}
\begin{align}
L_t &= 10\log\Big({{p_1^2 + p_2^2 + p_3^2}\over{p_0}^2}\Big)\\
&=10\log\Big[({{p_1}\over{p_o}})^2+({{p_2}\over{p_0}})^2+({{p_3}\over{p_0}})^2\Big]
\end{align}

한편 (1)식에서 좌변과 우변을 바꾸어 아래 (3)식과 같이 정리할 수 있을 것입니다.

\tag{3}
\begin{align}
10\log\Big({{p}\over{p_0}}\Big)^2 &= L_a\\
\log\Big({{p}\over{p_0}}\Big)^2 &={{L_a}\over{10}}\\
\Big({{p}\over{p_0}}\Big)^2 &= 10^{{L_a}\over{10}}\\
\Big({{p}\over{p_0}}\Big) &= \big(10^{{L_a}\over{10}}\big)^{1/2}
\end{align}

따라서 (3)식을 (2)식에 대입하면 아래의 (4)식이 얻어집니다. 이때 각 소음원마다의 압력진폭과 소음도를 반영하면 됩니다.

\tag{4}
\begin{align}
L_t &= 10\log\Big[\big(10^{{L_{a1}}\over{10}}\big)^{{1 \over 2} \cdot 2} + \big(10^{{L_{a2}}\over{10}}\big)^{{1\over 2 }\cdot 2} + \\
&~~~~~~~~~~~~~~~~~~\big(10^{{L_{a3}}\over{10}}\big)^{{1\over 2}\cdot 2} \Big]\\
&=10\log\big(10^{{L_{a1}}\over{10}} + 10^{{L_{a2}}\over{10}}+10^{{L_{a3}}\over{10}}\big)\\
\end{align}

결국 2개 이상의 소음원에서 방출된 소음도를 덧셈할 때에는 (4)식을 이용해서 합산해야 합니다.

2-2. 감산 공식

이번에는 감산하는 경우입니다. 기본적으로 가산하는 경우와 동일합니다만 빼내어지는 압력진폭 앞의 부호에 마이너스를 적용합니다.

예를 들어 기계음 L_{m}와 배경 소음 L_{bg}이 합쳐진 전체 소음도 L_t가 있습니다. 여기서 배경소음도를 빼내 기계의 소음도 L_m만을 계산하고 싶다면 다음 (5)식과 같이 식을 세워야 합니다.

이때 p_t는 기계음과 배경소음이 합쳐진 압력 진폭의 실효값이고, p_{bg}는 배경 소음만의 압력 진폭 실효값입니다.

\tag{5}
\begin{align}
L_m &= 10\log\Big({{p_t^2 - p_{bg}^2}\over{p_0}^2}\Big)\\
&=10\log\Big[({{p_t}\over{p_o}})^2-({{p_{bg}}\over{p_0}})^2\Big]
\end{align}

(3)식을 (5)식에 대입하면 아래의 (6)식이 얻어집니다.

\tag{6}
\begin{align}
L_m &= 10\log\Big[\big(10^{{L_{t}}\over{10}}\big)^{{1\over 2}\cdot2} - \big(10^{{L_{bg}}\over{10}}\big)^{{1\over 2}\cdot2}  \Big]\\
&=10\log\big(10^{{L_{t}}\over{10}} - 10^{{L_{bg}}\over{10}}\big)
\end{align}

결국 소음도를 뺄셈할때에는 (6)식을 이용해야 합니다.

3. 가산과 감산 연습문제

3-1. 가산 연습문제

(문제)

다음의 기계장치들에서 소음이 발생하고 있다. 첫번째 냉각기에서는 70 dB, 두번째 압축기에서는 72 dB, 세번째 압력펌프에서는 74 dB이 발생한다면 전체 소음도는 얼마가 되겠는가?

(풀이)

문제에서 세 기계장치들에 대한 음압 레벨이 각각 제시되어 있습니다. 이러한 음압 레벨을 (4)식을 이용하여 합하면 되겠죠.

\tag{7}
\begin{align}
L &= 10\log\big(10^{{L_{a1}}\over{10}} + 10^{{L_{a2}}\over{10}}+10^{{L_{a3}}\over{10}}\big)\\
&= 10\log\big(10^{{70~\mathrm{dB}}\over{10}} + 10^{{72~\mathrm{dB}}\over{10}}+10^{{74~\mathrm{dB}}\over{10}}\big)\\
&=10\log\big(10^{{7.0}} + 10^{{7.2}} + 10^{{7.4}}\big)\\
&=77~\mathrm{dB}
\end{align}

전체 소음도는 77 dB입니다.

3-2. 감산 연습문제

(문제)

기계장치들이 있는 옥상에서 측정된 전체 소음이 72.79 dB이다. 기계 장치들을 모두 정지한 상태에서 측정한 배경 소음이 65.00 dB이었다면 기계장치들만의 소음도는 얼마인가?

(풀이)

문제에서 전체 소음도와 배경 소음도가 각각 제시되었습니다. 전체 소음도에서 배경 소음도를 빼면 기계장치들의 소음도를 구할 수 있습니다.

소음도 감산에 대한 경우이므로 (6)식을 적용하면 됩니다.

\tag{8}
\begin{align}
L_m &=10\log\big(10^{{L_{t}}\over{10}} - 10^{{L_{bg}}\over{10}}\big)\\
&=10\log\big(10^{{72.79~\mathrm{dB}}\over{10}} - 10^{{65.00~\mathrm{dB}}\over{10}}\big)\\
&=10\log \big(10^{7.279} - 10^{6.500} \big)\\
&=72.00~\mathrm{dB}
\end{align}

기계장치의 소음도는 72.00 dB입니다.

마지막으로 소음도와 관련된 뉴스기사 하나를 링크합니다. 소음 피해를 입증하기 위해 소음도가 활용되는 것을 알 수 있습니다.

또한 등가소음도와 관련된 연습문제는 이곳으로 방문하세요.

Related posts.

등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요. 소음의 거리감쇠 공식 유도와 예제 풀이 전자기파 스펙트럼 대역의 구분, 특징과 활용 네이비즘 서버 시간 알림 사이트를 보고 떠오른 옛 추억과 표준 시간의 중요성 표준 오차 계산 예제 방향코사인 정의와 의미 만유인력 법칙에서 r이 물체 중심 사이의 거리인 이유 단열 과정 (adiabatic process)