Last Updated on 2021-11-12 by BallPen
벡터를 작도하는 방법과 수학적으로 엄밀히 표시하는 방법을 알아보겠습니다. 이를 통해 벡터의 크기와 벡터를 x와 ~y성분으로 분해하는 요령을 알 수 있어요.
벡터 성분 이란 2차원의 경우 벡터의 x와 ~y성분을 의미하고 3차원의 경우 x, ~y, ~z성분을 의미합니다. 이번 글에서는 물리학, 과학 및 공학 분야에서 자주 사용하는 벡터를 그림으로 작도하고 벡터의 크기와 성분을 분해하는 요령을 설명드립니다.
벡터 성분을 분해하는 방법은 크게 작도를 이용하는 방법과 수학적 방법의 두가지가 있습니다.
자세히 알아보죠. 쉬운 듯하면서도 어려운게 벡터에요. 목차는 다음과 같습니다.
혹시 시작하기에 앞서 단위벡터, 벡터의 정규화에 대해 궁금한 분은 여기를 클릭하세요.
Contents
1. 벡터 개념
1-1. 벡터 정의
아래 그림과 같이 마찰이 없는 아주 평탄한 바닥면을 상상해보세요. 그리고 그 바닥면 위에는 질량 m인 정지한 어느 물체가 있습니다.
만약 그 물체에 수평 방향으로 20 N의 일정한 힘 F_1이 작용한다고 생각해보세요. 여기서 힘이라고 하는 것은 물체를 밀거나 끄는 것을 말합니다.

이때 물체에 작용하는 물리량을 화살표로 표시한 것을 벡터(vector)라고 합니다. 벡터를 화살표로 표시하는 이유는 크기와 방향을 표현하기 쉽기 때문이에요.
반면에 크기만 있는 물리량을 스칼라(scalar)라고 합니다.
1-2. 벡터 설명
화살표의 길이는 벡터의 크기를 나타내고 화살표의 머리는 벡터가 작용하는 방향을 뜻합니다. 위 그림에서도 화살표를 볼 수 있는데요. 화살표의 길이는 힘의 크기 20 N을 의미하고, 화살표의 머리는 힘이 작용하는 방향입니다. 또한 화살표의 시작점은 힘이 작용하는 지점을 나타냅니다.
그렇다면 이러한 벡터 화살표를 직접 방안지에 그릴 수 있을까요? 네 그릴 수 있습니다. 직접 그림을 그려보면 이해하기 훨씬 쉬워요.
2. 벡터 표기법 : 작도를 통한 벡터 표시 방식
2-1. 수평방향으로 작용하는 힘
– 벡터 작도
마찰이 없는 바닥 위에 놓여진 택배 상자를 생각해 보세요. 그런데 그 택배상자에 수평방향으로 F_1 = 20.0~\mathrm{N}의 힘이 작용한다고 보겠습니다. (유효숫자를 3개로 쓰겠습니다. 사진에서 20N을 20.0N으로 작성했어야 했는데 제가 실수했습니다.)
하늘에서 내려다 본 방향으로 그림을 그리면 아래 사진처럼 보일거에요. 아래 사진에서 사각형 모양이 택배상자에요. 택배상자의 크기가 크더라도 적당하게 작게 줄여서 그리면 됩니다.
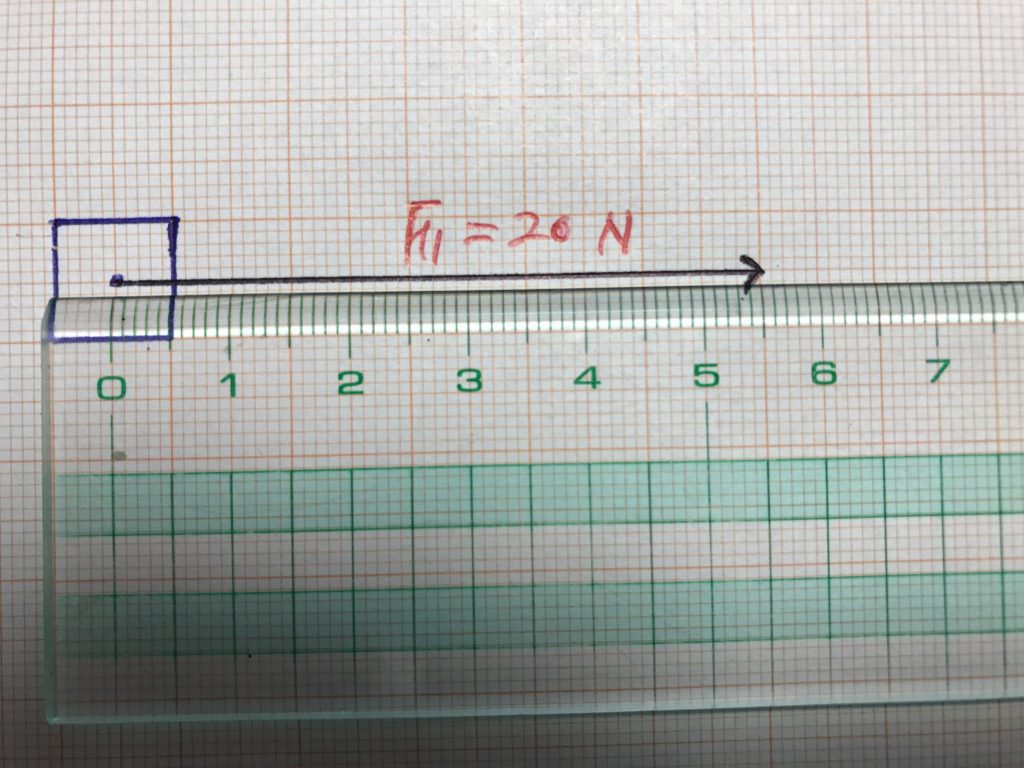
그럼 얼마나 작게 그려야 하나요? 그것은 여러분 마음입니다. 한변을 1 cm로 그리고 싶으면 1 cm로 그리고, 한변을 2 cm로 그리고 싶으면 2 cm로 그리면 됩니다. 여러분 마음대로 그려보세요.
택배상자에 수평 방향으로 힘이 작용하면 택배상자가 정지상태에서 힘이 작용하는 방향으로 움직이게 될거에요. 그래서 일반적으로 힘이 작용하는 지점은 택배상자의 중간지점으로 봅니다.
그래서 택배상자에 수평방향으로 작용하는 힘의 벡터는 위 사진처럼 상자의 중간지점부터 그리면 됩니다. 이때 화살의 머리는 힘이 작용하는 방향을 향하면 되겠죠.
이제 자를 대고 화살의 길이을 그리면 되는데요. 많은 사람들이 사각형의 중심에 볼펜을 대고 고민하는 경우가 많아요. 무엇을 고민하냐면, 도대체 얼마나 길게 그려야 20.0 N이 되는지를 고민합니다.
정답은 여러분 맘대로 그리시면 되요. 위 사진은 20.0 N의 힘의 크기를 55.0 mm로 그렸어요. 이렇게 그린 이유는 제가 그렇게 정했기 때문입니다. 기준을 이렇게 정했으면 만일 10.0 N을 그린다면 어떻게 그리면 될까요? 바로 27.5 mm로 그리면 됩니다.
그렇다면 1.0 N을 그린다면 어떻게 그리면 될까요? 네 맞아요 2.75 mm만큼만 화살의 길이를 그리면 됩니다. 이와 같이 크기가 1.0 N인 벡터를 단위벡터(unit vector)라고 합니다.
– 벡터 성분
이제는 벡터의 성분을 이야기 해보겠습니다. 벡터의 성분이란 벡터를 x성분과 y성분으로 분해하는 것을 말합니다. 수학에서 좌표를 공부해보셨을거에요. 예를 들어 (3,4)의 좌표는 x방향으로 3칸, y방향으로 4칸을 이동한 좌표를 뜻하는 거잖아요.
그거하고 똑같습니다. 벡터도 x와 y성분으로 쪼개면 계산할 때 편리함이 많아요.
위의 사진은 x 방향으로 20.0 N의 힘이 작용하고 있음을 나타냅니다. 반면에 y방향으로는 아무런 작용하는 힘이 없어요. 따라서 F_1 = 20.0~\mathrm{N}의 힘은 다음과 같이 성분으로 나타낼 수 있습니다.
\tag{1}
\begin{align}
F_{1x} &= 20.0~\mathrm{N}\\
F_{1y} &= 0.0~\mathrm{N}
\end{align}이제 물체에 하나의 수평한 힘이 작용할 때 그 힘에 대한 벡터 성분을 잘 표현할 수 있게 되었습니다.
2-2. 비스듬히 작용하는 힘
– 벡터 작도
이번에는 힘이 기준축으로부터 비스듬하게 작용하는 경우를 보겠습니다.
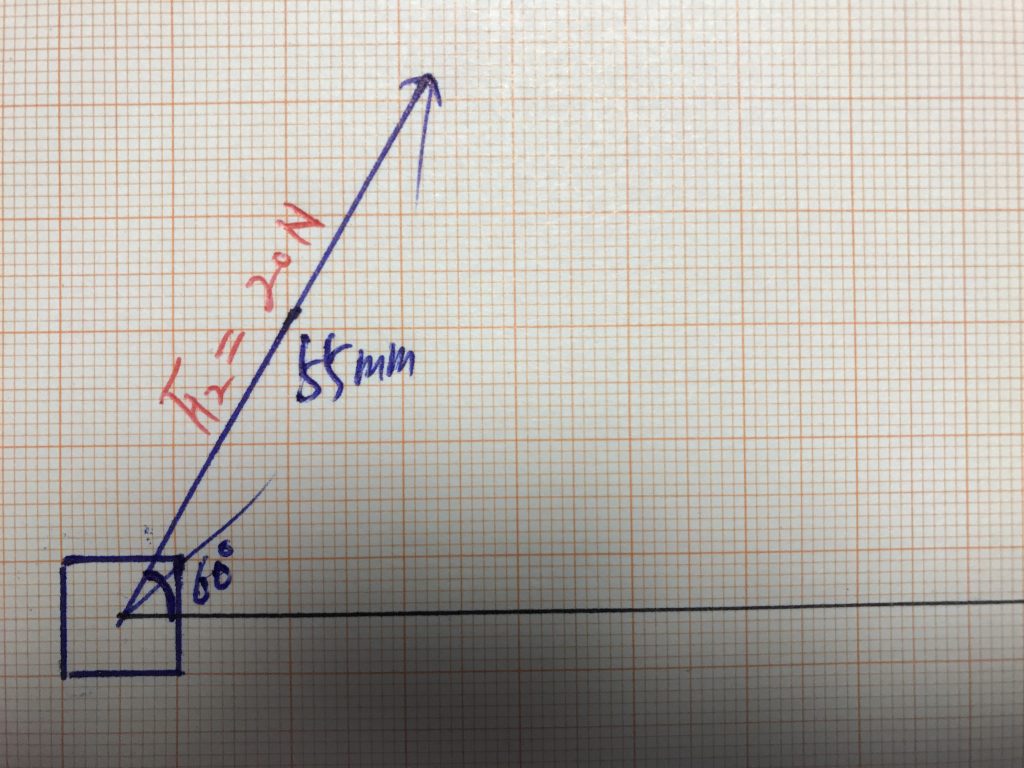
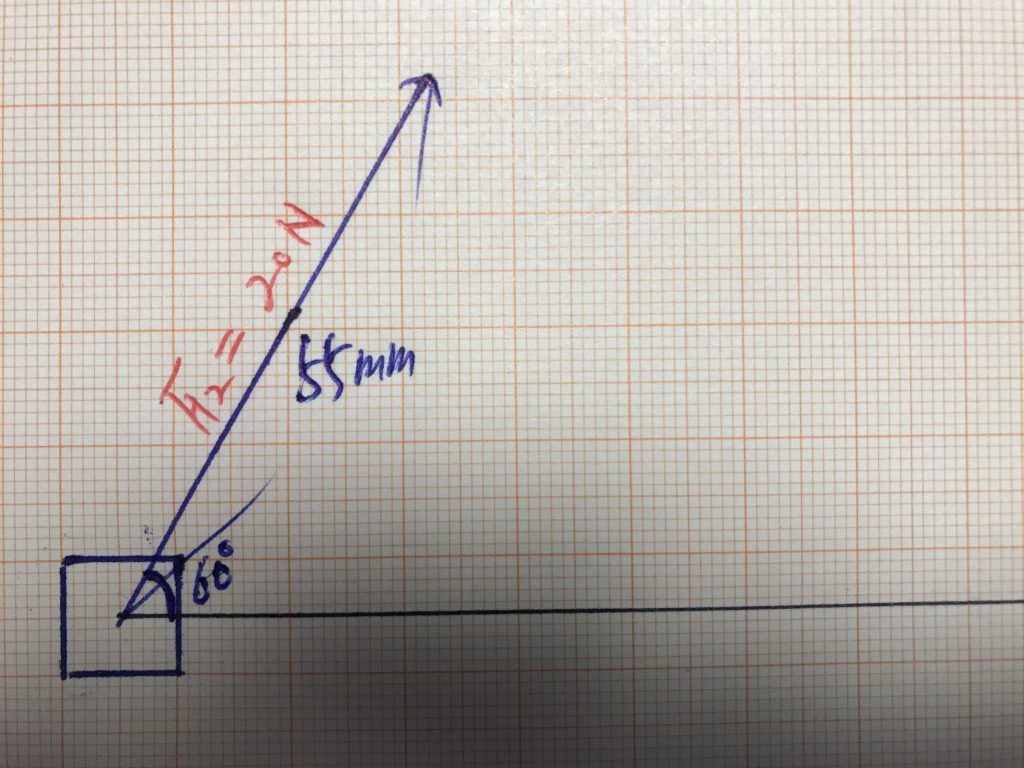
아래 사진도 위에서 내려다본 택배상자를 그림으로 그린 것입니다. 이때 힘이 작용하는 방향으로 화살표가 그려져 있어요.
즉 F_2 = 20.0~\mathrm{N}의 힘이 작용하고 있어요. 여기에서도 20.0 N의 힘의 크기를 화살표의 길이 55.0 mm로 작도한 것을 알 수 있습니다.
그런데 힘의 방향이 가로축으로부터 60^\circ 만큼 틀어져 있어요. 즉 바로 위 사진에서 힘이 작용하는 방향을 기준으로 할 때 아래 사진에서는 힘이 작용하는 방향이 60^\circ 돌아가 있는 것입니다.
이러한 경우를 비스듬히 작용하는 힘이라고 말합니다.
– 벡터 성분
이번에는 비스듬히 작용하는 힘에 대한 벡터 성분을 구해 보겠습니다.
위 사진에서 주어진 벡터 F_2의 x와 y성분은 어떻게 구할 수 있을까요? 바로 작도를 통해 구할 수 있습니다. 힘 F_2를 빗변으로 하는 직각삼각형을 그리면 됩니다.
그 결과는 아래 사진과 같습니다.
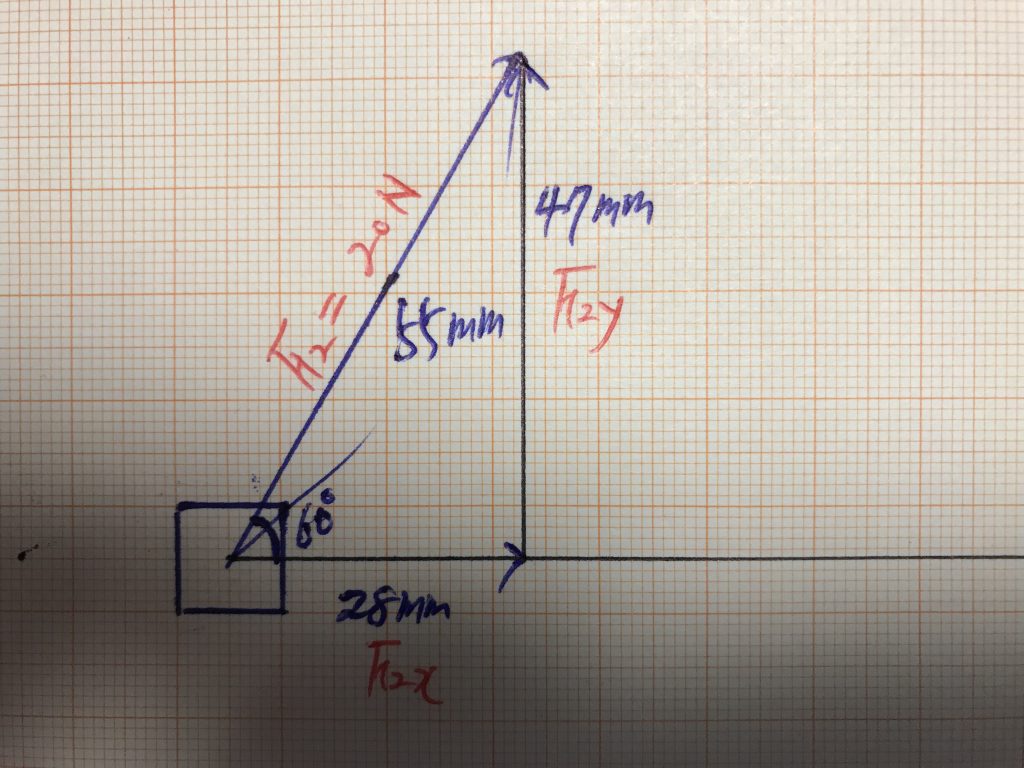
사진과 같이 빗변의 길이가 55.0 mm인데 그것의 힘의 크기를 20.0 N으로 두었잖아요. 그런데 직각삼각형을 그린 후 밑변의 길이를 측정했더니 28.0 mm로 측정되었습니다. 이것이 x방향으로 작용하는 힘의 크기 F_{2x}입니다. 비례식을 이용해 그 힘의 크기를 구해보겠습니다.
\tag{2}
\begin{align}
55.0~\mathrm{mm} : 20.0~\mathrm{N} &= 28.0~\mathrm{mm} :F_{2x}\\
F_{2x}&={{28.0~\mathrm{mm}\times20.0~\mathrm{N}}\over{55.0~\mathrm{mm}}}\\
&=10.2~\mathrm{N}
\end{align}바로 10.2 N이 나왔습니다. 이번에는 직각삼각형의 높이 47.0 mm에 대응하는 F_{2y}의 크기를 구해보겠습니다. 동일하게 비례식을 적용하면 됩니다.
\tag{3}
\begin{align}
55.0~\mathrm{mm} : 20.0~\mathrm{N} &= 47.0~\mathrm{mm} :F_{2y}\\
F_{2y}&={{47.0~\mathrm{mm}\times20.0~\mathrm{N}}\over{55.0~\mathrm{mm}}}\\
&=17.1~\mathrm{N}
\end{align}바로 17.1 N이 나왔습니다. (2)와 (3)식으로 구한 각 성분의 크기를 정리하면 아래와 같습니다.
\tag{4}
\begin{align}
F_{2x} &= 10.2~\mathrm{N}\\
F_{2y} &= 17.1~\mathrm{N}
\end{align}자 이렇게 해서 간단하게 벡터를 그림으로 작도하고 성분을 분해하는 방법에 대해 알아보았습니다. 자와 각도기만 있다면 벡터를 그림으로 그리고 성분을 쉽게 분해할 수 있게 되었어요.
그러나 문제가 하나 있는데요. 자와 각도기를 사용해서는 벡터의 크기, 성분의 크기 등을 정확히 측정하기 어렵다는데 문제가 있습니다. 왜냐면 눈금을 정밀하게 읽는데는 한계가 있으며 계통 오차를 포함할 수 밖에 없습니다.
그래서 수학적 방법을 통해 벡터를 표기하고 성분을 분해하는 것을 더 자주 사용합니다.
3. 벡터 표기법 : 수학적 방법을 통한 벡터 표시 방식
3-1. 수평방향으로 작용하는 힘
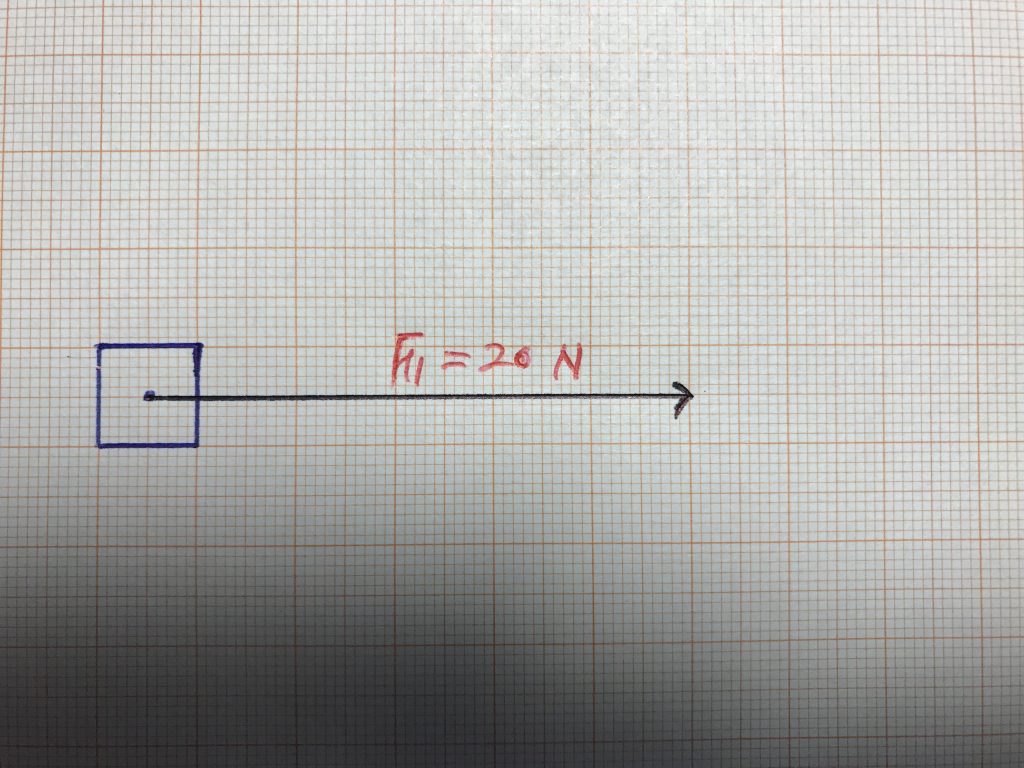
위 사진은 20.0 N의 힘이 물체에 수평방향으로 작용하고 있음을 작도한 것입니다.
이것을 수학적으로 어떻게 성분을 표기하고 또 벡터는 어떻게 표기하는지 알아보겠습니다. 우선 벡터의 성분 표기를 먼저 알아보겠습니다.
– 벡터의 성분 표기
위 사진처럼 수평방향 즉 가로방향으로만 힘이 존재하는 경우에는 (1)식 처럼 표기해도 틀리지 않습니다.
다만 수학을 사용하고 있으니 보다 엄밀한 물리적 표기법을 사용하면 다음과 같이 표기할 수 있어요.
벡터는 크기와 방향을 모두 갖고 있는 물리량이므로 이 둘을 모두 수치 표현에 반영하는 것입니다. 바로 아래 (5)식 처럼 벡터의 크기와 x와 y방향의 단위 벡터(크기가 1인 벡터)를 이용해서요.
\tag{5}
\begin{align}
\vec{F}_{1x} &=크기 \times x방향의 ~단위벡터\\
&= 20.0 \times \hat{x}\\
&=20.0\hat{x} ~\mathrm{N}\\
\vec{F}_{1y} &= 크기 \times y방향의~단위벡터\\
&=0.0 \times \hat{y}\\
&=0.0 \hat{y} ~\mathrm{N}
\end{align}– 벡터의 표기
그렇다면 (5)식의 성분들을 갖는 벡터 \vec{F}_{1}의 표기는 어떻게 하면 될까요? 바로 아래와 같이 (5)식에서 구한 x성분과 y성분의 합으로 표현하면 됩니다. 이때 성분들의 차도아니고 곱도 아닌 합을 하는 이유는 나중에 벡터 합에서 구체적으로 이해할 수 있습니다.
\tag{6}
\begin{align}
\vec{F}_1 &= \vec{F}_{1x} + \vec{F}_{1y}\\
&=(20.0\hat{x} + 0.0\hat{y})~\mathrm{N}
\end{align}작도는 직관적으로 이해하기는 쉽지만 간결하지 않다는 단점이 있는데요. (6)식과 같이 표현하니 아주 간결한 벡터 표현이 얻어졌습니다.
3-2. 비스듬히 작용하는 힘
위 사진은 x축으로부터 60^\circ 방향으로 20.0 N의 힘이 작용하고 있는 것을 나타낸 작도입니다. 이에 대해서도 수학적인 성분 표기와 벡터 표현을 알아보겠습니다.
일단 위 사진에 있는 벡터의 x성분과 y성분의 크기는 (4)식으로 구했었습니다. 그러나 자로 직각삼각형의 밑변의 길이와 높이의 길이를 측정하다 보니 정확한 측정이 불가능하다고 말했었습니다.
– 벡터의 성분 표기
그러나 수학의 삼각함수를 사용하면 정확하게 계산할 수 있어요. 아래의 (7)식 처럼요.
\tag{7}
\begin{align}
\vec{F}_{2x} &=x방향~크기 \times x방향 ~단위벡터\\
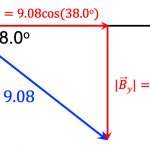
&= F_{2}\cos\theta \times \hat{x}\\
&= 20.0 \cos 60^\circ \hat{x}\\
&= 10.0 \hat{x}~\mathrm{N}\\
\vec{F}_{2y} &=y방향~크기 \times y방향 ~단위벡터\\
&= F_{2}\sin\theta \times \hat{y}\\
&= 20.0 \sin 60^\circ \hat{y}\\
&= 17.3\hat{y}~\mathrm{N}\\
\end{align}(7)식과 (4)식의 결과를 비교해 보세요. (7)식이 삼각함수를 이용해 정확하게 구해진 것입니다. 반면에 (4)식은 오차를 포함하고 있어요.
– 벡터의 표기
그렇다면 (7)식의 성분들을 갖는 벡터 \vec{F}_{2}의 표기는 어떻게 하면 될까요? 바로 아래의 (8)식과 같이 (7)식에서 구한 x성분과 y성분의 합으로 표현하면 됩니다.
\tag{8}
\begin{align}
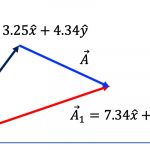
\vec{F}_2 &= \vec{F}_{2x} + \vec{F}_{2y}\\
&=(10.0\hat{x} + 17.3\hat{y})~\mathrm{N}
\end{align}4. 요약
- 벡터란 크기와 방향을 갖는 물리량을 말한다.
- 힘벡터를 작도할 때에는 벡터의 작용점, 크기, 방향을 모두 고려해야 한다. 특히 벡터의 크기는 한번 정하면 다른 크기를 표현할 때에도 기준 벡터에 비례해서 크기를 표현해야 한다.
- 벡터 성분은 벡터를 x성분과 y성분으로 분해하는 것을 말한다. 작도법에서는 직각삼각형을 그린 후 각 성분의 길이를 자로 측정하여 성분별 힘의 크기를 구한다. 수학적 방법에서는 삼각함수를 이용하여 각 성분의 힘의 크기를 구한다.
- 벡터 표기법은 각 성분별로 구해진 힘의 크기를 벡터 합하여 표기한다.
5. 벡터 관련 추천 글
- 벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분
- 단위벡터 의미와 벡터 정규화
- 벡터의 방향 표기를 정확하게 하는 방법
- 벡터의 덧셈 : 기하학적 표현과 수학적 처리
- 벡터의 뺄셈 : 벡터의 변화량을 구하는 방법

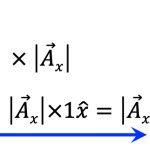



10 thoughts on “벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분”