교류신호 – 순간값, 최대값, P-P값, 평균값, 실효값의 의미와 공식

Last Updated on 2024-06-13 by BallPen

사인파형 교류신호의 크기를 표현하는 다양한 용어들이 있는데요. 이번에는 그 용어들의 의미와 공식을 알아봅니다.

교류신호 또는 교류(AC, Alternating Current)란 전류 또는 전압의 크기와 방향이 시간에 따라 주기적으로 변하는 신호를 말합니다.

이때 교류신호의 크기를 표현하는 다양한 용어들이 있는데요.

이번 글에서는 사인파형 교류 신호의 다양한 크기 표현 용어들이 갖는 의미와 관련 공식을 알아보겠습니다.

다음은 목차입니다.

1. 교류신호 모양과 수학적 표현

교류신호는 위에서 말씀드린대로 전류 또는 전압이 시간에 따라 크기와 방향이 주기적으로 변하는 신호를 말합니다.

신호의 모양은 사각파, 삼각파 등 다양하게 존재할 수 있는데요. 보통은 아래 [그림 1]에 제시된 사인파형 교류 신호가 많이 사용됩니다.

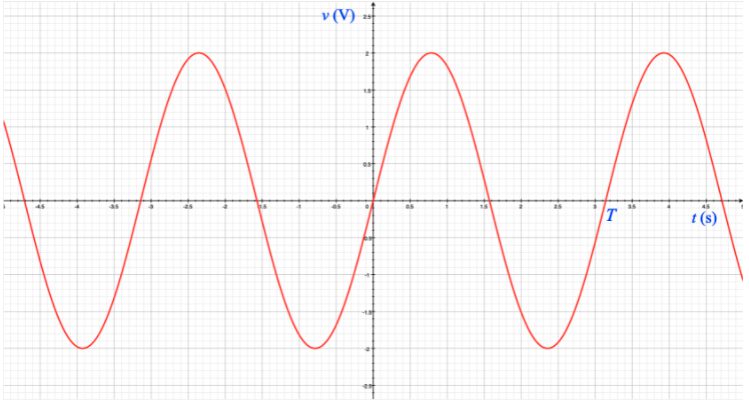
[그림 1] 사인파형 교류신호 모양. 전압 v가 시간 t에 따라 변하고 있어요. 그림에 표기된 T는 신호가 한번 진동하는데 걸리는 시간인 주기를 의미합니다.

[그림 1]은 y축의 전압신호 v가 x축의 시간 t에 따라 오르락 내리락 하며 전압의 크기가 주기적으로 변하는 것을 보여주고 있어요.

또한 그림에 표시된 한 주기 T의 절반은 양의 전압을 나머지 절반은 음의 전압을 갖게 됩니다. 이것은 회로에 흐르는 전류의 방향이 시간에 따라 바뀐다는 것을 뜻합니다.

그렇다면 이러한 사인파형 교류신호의 수학적 표현은 어떻게 될까요? 바로 아래 식과 같이 표현됩니다.

\tag{1}
\begin{align}
v=V_p \sin(\omega t)
\end{align}

즉 V_p와 \omega만 정의되면 교류신호가 만들어지는거에요. 이때 두 양이 무엇인지는 아래쪽에 별도로 설명드릴게요. 일단 넘어가셔요.

[그림 1]에 그려진 빨강색 교류신호는 아래 (2)식의 함수를 이용해 그려진 거에요.

\tag{2}
\begin{align}
v=2 \sin (2t)
\end{align}

이제부터 교류신호의 크기를 표현하는 다양한 용어들을 알아보겠습니다.

2. 교류신호 크기 표현

교류신호의 크기를 표현한다는 것이 무슨 의미인지 생소할 수 있어요.

우선 직류신호의 크기 표현부터 잠깐 알아봐요. 아래 [그림 2]는 이상적인 직류신호의 모습을 파랑색 선으로 나타낸 것입니다. 이 직류신호의 크기는 몇 V일까요?

이렇게 물으면 당연히 2.4 V라고 말할 것입니다. 왜냐면 시간이 변하더라도 2.4 V가 일정하게 유지되니까 2.4 V라고 하는 거에요.

[그림 2] 전형적인 직류신호 모양. 2.4 V의 전압이 시간에 무관하게 일정하게 유지됩니다.

이와 같이 어느 신호가 주어졌을 때 그 신호가 어느 정도의 크기를 갖느냐를 표현하는 방법이 신호의 크기입니다. 이와 같이 직류는 어렵지 않게 신호 크기를 정의할 수 있어요.

문제는 교류입니다.

아래 [그림 3]은 [그림 1]의 일부분을 확대한 그림인데요. 이 교류신호의 크기는 몇 V일까요?

[그림 3] 교류신호

교류신호는 [그림 3]과 같이 시간에 따라 크기가 계속 변하므로 뭐라고 하나의 값을 이용해 표현하기 어려워요.

예를 들어 0 s인 순간에는 0 V이고요. 0.8 s근처에서는 2 V정도가 된다는 것을 알 수 있어요. 또한 1.6 s 근처에서는 전압이 다시 0V가 되고, 2.35 s 정도에서는 -2 V가 됩니다. 또한 3.13 s 정도에는 다시 0 V가 됩니다.

그래서 과학자들은 교류신호 크기 표현 방법을 정의하게 되었는데요.

그 방법에는 순간값, 최대값, P-P값, 평균값, 실효값이 사용된답니다. 하나하나 알아보겠습니다.

2-1. 순간값 (순시값)

순간값은 몇 s인 순간에 교류신호가 몇 V인가를 나타내는 표현법입니다. 위에서 말씀드렸듯이 0 s인 순간에 0 V, 0.8 s인 순간에 2 V, 1.6 s인 순간에 0 V라고 할때 이때 사용되는 전압값이 바로 순간값입니다.

결국 순간값은 시간에 따라 순간 순간 달라지는 교류신호의 크기 표현입니다. 순간값을 다른 말로 순시값이라고도 많이 불러요.

순간값은 수식을 이용하면 정확하게 구할 수 있어요. 예를 들어 (2)식의 교류신호 식이 있을때 알고 싶은 시간을 t에 대입하면 됩니다.

예를 들어 1.3 s인 순간의 순간값 v를 구하기 위해서는 아래와 같이 계산하면 됩니다. 이때 주의할 것은 sin값은 라디안(radian)으로 계산해야 한다는 거에요.

\tag{3}
\begin{align}
v &=V_p \sin (\omega t)\\ 
&=2 \sin (2t)\\
&=2 \sin(2 \times 1.3)\\
&=2 \sin(2.6 ~\mathrm{rad})\\
&\approx1.03 ~\mathrm{V}
\end{align}

순간값이 약 1.03 V가 나오는군요. 이 결과는 [그림 3]에서 1.3 s인 순간의 v값과 같습니다.

2-2. 최대값

최대값은 교류신호의 크기를 하나의 대표 수치로 표현하는데 많이 사용됩니다.

[그림 4] 교류신호에서 최대값 V_p는 신호의 꼭대기로부터 x축 사이의 전압을 말합니다.

[그림 4]에서 V_p로 표시한 것과 같이 최대값은 신호의 가장 꼭대기로부터 x축 사이의 전압을 말합니다. 그러므로 순간값처럼 시간에 따라 달라지는 값이 아닙니다.

참고로 V_p에서 아래첨자 p는 peak의 머리글자입니다.

그렇다면 [그림 4]에서 보여지는 교류신호의 최대값 V_p는 얼마일까요? 바로 2 V임을 알 수 있습니다.

수학적으로 최대 전압 V_p는 공식에서 아주 쉽게 드러납니다. (1)식과 (2)식을 다시 쓰면 아래와 같습니다.

\tag{4}
\begin{align}
v &=V_p \sin (\omega t)\\ 
&=2 \sin (2x)\\
\end{align}

식으로부터 V_p가 2 V임을 알 수 있습니다.

교류신호 크기가 최대값으로 측정되었다면 반드시 최대값으로 측정된 것임을 알려야 합니다.

예를 들어 “교류신호의 최대값은 2 V입니다“와 같이요. 만일 “교류신호의 크기는 2 V입니다”라고만 표기하면 부족한 정보전달이 됩니다. 아래를 더 보시면 이해하시겠지만 의미가 완전히 달라질 수 있어요.

2-3. P-P값

P-P값은 교류신호의 크기를 하나의 대표 수치로 표현하는 또 하나의 방법입니다.

[그림 5] 교류신호에서 P-P값인 V_{p-p}는 신호의 꼭대기로부터 가장 낮은 지점(반대쪽 꼭대기)사이의 전압을 말합니다.

[그림 5]에서 V_{p-p}로 표시한 P-P값은 신호의 가장 꼭대기로부터 가장 낮은 지점(반대쪽 꼭대기) 사이의 전압을 말합니다. 그러므로 최대값의 두배가 되는 것이죠.

참고로 V_{p-p}에서 아래첨자 p-p는 peak to peak의 머리글자입니다.

그렇다면 [그림 5]에서 보여지는 교류신호의 P-P값 V_{p-p}는 얼마일까요? 바로 최대값의 2배인 4 V임을 알 수 있습니다.

공식으로는 최대값 V_p를 이용하여 아래와 같이 주어집니다.

\tag{5}
\begin{align}
V_{p-p} &= 2V_p\\
&=2 \times 2 ~\mathrm{V}\\
&=4 ~\mathrm{V}
\end{align}

교류신호 크기가 P-P값으로 측정되었다면 반드시 P-P값으로 측정된 것임을 알려야 합니다.

예를 들어 “교류신호의 P-P값은 4 V입니다“와 같이요. 만일 “교류신호의 크기는 4 V입니다”라고만 표기하면 잘못된 정보전달이 됩니다. 독자 입장에서는 4 V가 최대값인지 P-P값인지 모르기 때문이죠.

2-4. 평균값

평균값은 교류신호의 크기를 하나의 대표 수치로 표현하는 또 하나의 방법입니다.

교류신호는 계속 말씀드리는것과 같이 크기가 시간에 따라 계속 달라집니다. 그래서 이렇게 달라지는 교류신호의 크기를 하나의 수치로 표현하기 위해 평균을 낼수가 있을거에요.

그렇다면 (1)식으로 주어진 사인꼴 교류신호의 평균값은 얼마일까요? 사인꼴 신호는 하나의 주기 신호가 계속 반복되므로 한주기 T에 걸친 평균을 내보도록 하겠습니다.

\tag{6}
\begin{align}
V_{avg}&={{1}\over{T}}\int_{0}^{T} v dt\\ 
&= {{1}\over{T}}\int_{0}^{T} V_p \sin(\omega t) dt\\ 
&={{V_p}\over{T}}\int_{0}^{T}  \sin(\omega t) dt\\
&={{V_p}\over{T}} \Big[   -{{1}\over{\omega}} \cos (\omega t)   \Big]_{0}^{T}\\
&={{V_p}\over{T}} \Big[   -{{1}\over{2 \pi/T}} \cos ({{2 \pi}\over{T}} t)   \Big]_{0}^{T}\\
&=-{{V_p}\over{2 \pi}} \big(\cos(2 \pi) - \cos(0) \big)\\
&=-{{V_p}\over{2 \pi}} \big(1 - 1 \big)\\
&=0
\end{align}

이때 (6)식의 4번째 줄에서 \omega를 2\pi / T로 바꾸었어요. 그 이유는 \omega가 각진동수이기 때문입니다.

(6)식과 같이 한주기에 걸친 사인파형 교류신호의 평균은 0 V가 됩니다. 그 이유는 반주기 동안 곡선아래의 면적이 양의 값이 되고 나머지 반주기 동안 음의 값이 되어 두 값을 합하면 서로 상쇄되기 때문입니다.

이와 같이 한주기에 걸쳐 평균을 내면 모든 교류신호는 0 V가 됩니다. 이러한 문제를 해소하기 위해 교류신호의 평균값은 한주기가 아닌 반주기에 걸친 평균값을 사용합니다.

구체적인 방법은 아래 (7)식과 같으며, 그 결과는 최대전압 V_p의 0.637배가 됩니다.

\tag{7}
\begin{align}
V_{avg} &= {{1}\over{T/2}}\int_{0}^{T/2} V_p \sin(\omega t) dt\\ 
&={{2V_p}\over{T}}\int_{0}^{T/2}  \sin(\omega t) dt\\
&={{2V_p}\over{T}} \Big[   -{{1}\over{\omega}} \cos (\omega t)   \Big]_{0}^{T/2}\\
&={{2V_p}\over{T}} \Big[   -{{1}\over{2 \pi/T}} \cos ({{2 \pi}\over{T}} t)   \Big]_{0}^{T/2}\\
&=-{{V_p}\over{\pi}} \big(\cos(\pi) - \cos(0) \big)\\
&=-{{V_p}\over{\pi}} \big(-1 - 1 \big)\\
&={{2}\over{\pi}}V_p\\
&=0.637~ V_p
\end{align}

그러므로 최대값 V_p가 2 V인 경우 평균값은 아래와 같이 1.274 V가 됩니다.

\tag{8}
\begin{align}
V_{avg} &= 0.637~V_p\\
&=0.637 \times 2~\mathrm{V}\\
&=1.274~\mathrm{V}
\end{align}

교류신호 크기가 평균값으로 측정되었다면 반드시 평균값으로 측정된 것임을 알려야 합니다.

예를 들어 “교류신호의 평균값은 1.274 V입니다“와 같이요. 만일 “교류신호의 크기는 1.274 V입니다”라고만 표기하면 잘못된 정보전달이 됩니다. 독자 입장에서는 1.274 V가 최대값인지 P-P값인지 평균값인지 모르기 때문입니다.

2-5. 실효값

이번에는 실효값을 알아보겠습니다. 실효값도 교류신호의 크기를 대표 수치로 표현하는 방법 중의 하나입니다.

실효값의 도입 배경

앞서 설명드린 최대값과 P-P값은 파형의 모습으로부터 도출된 개념이고 평균값은 신호의 크기가 시간에 따라 변하니 반주기에 걸쳐 평균을 내는 개념입니다.

이에 비해 실효값은 직류에서 정의된 공식들과 교류에서 정의되는 공식들이 서로 같아지게끔 하기 위해 도입된 개념으로 보시면 좋습니다. 만일 실효값이 정의되지 않았다면 교류를 공부하는 것이 쉽지 않았을거에요.

예를 들어, 직류회로의 저항에서 소모되는 전기에너지 W에 관한 식을 생각해보죠. 저항에서 소모되는 전력을 P, 시간을 t, 직류전압을 V, 직류전류를 I, 저항을 R이라고 하면 아래 (9)식이 성립합니다.

\tag{9}
\begin{align}
W&=Pt\\
&=VIt\\
&=V\big({{V}\over{R}} \big)t\\
&={{V^2}\over{R}}t
\end{align}

그렇다면 직류에서 성립하는 (9)식이 교류에서도 동일하게 성립할까요? (9)식의 가장 끝 공식에서 저항 R과 시간 t는 직류이던 교류이던 차이가 없어요. 문제는 교류신호의 크기 V인데요.

이 교류신호의 크기 V를 어떻게 설정해야 (9)식의 공식 형태를 교류에서도 똑같이 사용할 수 있을까요? 이 때문에 도입된 것이 실효값입니다.

실효값 공식 유도

실효값을 정의하기 위해서는 (9)식을 아래와 같이 적용해보죠. 다만 시간 t는 한주기 T로 설정하겠습니다.

\tag{10}
\begin{align}
W={{V_{rms}^2}\over{R}} T = \int_{0}^{T}{{v^2}\over{R}} dt
\end{align}

여기서 V_{rms}값이 실효값으로 우리가 최종적으로 구할 값이에요. 가장 우변은 순간값 v가 시간에 따라 변하므로 적분을해야 가운데 식하고 개념이 같아지죠.

바꾸어 말씀드리면 (10)식의 가장 오른쪽 식이 교류신호에 의한 전기에너지 식이에요. 그런데 이 식을 직류에서 사용하는 (10)식의 가운데 식 형태로 표현하고 싶은거에요. 그러기 위해서 실효값 V_{rms}가 얼마가 되어야 하는지를 구하는 과정으로 보시면 됩니다.

(10)식에서 R을 약분하고 정리하면 아래 (11)식처럼 표현될거에요. 이때 근호안의 공식을 보면 v를 제곱한 값을 한주기에 걸쳐 평균하는 식임을 알 수 있어요(식(6)의 평균 구하는 식하고 형태가 동일합니다).

\tag{11}
\begin{align}
V_{rms} &= \sqrt{{{1}\over{T}}\int_{0}^{T} v^2 dt}\\

\end{align}

따라서 실효값 V_{rms}는 v를 제곱한 후 평균을 구한 값에 제곱근을 취하는 형태로 나타납니다. 이것을 미국식으로 표현하면 root mean sqare가 됩니다. 머리글자를 따면 rms가 되어 실효값 표현에 사용되고 있어요.

아무튼 (11)식을 계속 정리해보겠습니다. 중간에 삼각함수 항등식 중 두배각 공식이 적용됩니다.

\tag{12}
\begin{align}
V_{rms} &= \sqrt{{{1}\over{T}}\int_{0}^{T} v^2 dt}\\
&=\sqrt{{{1}\over{T}}\int_{0}^{T}  \big(V_p \sin (wt)\big)^2 dt}\\
&=\sqrt{{{V_p^2}\over{T}}\int_{0}^{T}  \sin^2 (wt) dt}\\
&=\sqrt{{{V_p^2}\over{T}} \int_{0}^{T} {{1-\cos(2 \omega t)}\over{2}} dt}\\
&=\sqrt{{{V_p^2}\over{2T}} \int_{0}^{T} {{1-\cos(2 \omega t)}} dt}\\
&=\sqrt{{{V_p^2}\over{2T}} \Big[ t- {{1}\over{2 \omega}} \sin(2 \omega t)\Big]_{0}^{T} }\\
&=\sqrt{{{V_p^2}\over{2T}} \Big[ t- {{1}\over{2 (2\pi/T)}} \sin(2 {{2\pi}\over{T}} t)\Big]_{0}^{T} }\\
&=\sqrt{{{V_p^2}\over{2T}} \big[(T-{{T}\over{4 \pi}}\sin(4\pi))-(0-{{T}\over{4\pi}}\sin(0) \big] }\\
&=\sqrt{{{V_p^2}\over{2T}} \big[(T-0)-(0-0) \big] }\\
&=\sqrt{{V_p^2}\over{2}}\\
&={{V_p}\over{\sqrt{2}}}
\end{align}

모두 정리했더니 실효값 V_{rms}는 최대전압 V_p를 \sqrt{2}로 나누면 구할 수 있습니다.

그러므로 최대값 V_p가 2 V인 경우 실효값은 아래와 같이 1.414 V가 됩니다.

\tag{13}
\begin{align}
V_{rms} &= {{V_p}\over{\sqrt2}}\\
&={{2~\mathrm{V}}\over{\sqrt{2}}}\\
&=1.414~\mathrm{V}
\end{align}

교류신호 크기가 실효값으로 측정되었다면 실효값으로 측정된 것임을 알리는 것이 좋습니다.

예를 들어 “교류신호의 실효값은 1.414 V입니다“와 같이요. 만일 “교류신호의 크기는 1.414 V입니다”라고만 표기하면 독자 입장에서는 1.414 V가 최대값인지, P-P값인지, 평균값인지, 실효값인지 모르기 때문입니다.

사실 특별한 언급이 없으면 일반적인 경우 실효값으로 간주한답니다.

3. 교류신호 크기 표현 예제

(예제)가정에서 사용하는 교류 전기 신호를 식으로 표현하면 v=311.1\sin({376.8 t})로 주어진다. (a)이 교류신호가 3.700 s인 순간의 전압은 얼마인가? (b)이 교류신호의 최대값은 얼마인가? (c) P-P값은 얼마인가? (d)평균값은 얼마인가? (e)실효값은 얼마인가?

(풀이)

(a) 3.700 s인 순간의 순간값은 다음과 같이 -202.1 V입니다..

\tag{14}
\begin{align}
v&=311.1 \sin(376.8 t)\\
&=311.1 \sin (376.8 \times 3.700)\\
&=-202.1~\mathrm{V}
\end{align}

(b) 최대값은 식에서 이미 주어져 있습니다. 311.1 V가 최대값입니다.

\tag{15}
V_p = 311.1 ~\mathrm{V}

(c) P-P값은 다음과 같이 최대값의 2배입니다.

\tag{16}
\begin{align}
V_{p-p} &= 2 V_p\\
&=2 \times 311.1~ \mathrm{V}\\
&=622.2~\mathrm{V}
\end{align}

(d)평균값은 최대값의 0.637배입니다.

\tag{17}
\begin{align}
V_{avg} &= 0.637~V_p\\
&=0.637 \times 311.1~\mathrm{V}\\
&=198.2~\mathrm{V}
\end{align}

(e)실효값은 최대값 V_p를 \sqrt{2}로 나누면 됩니다.

\tag{18}
\begin{align}
V_{rms} &= {{V_p}\over{\sqrt2}}\\
&={{311.1~\mathrm{V}}\over{\sqrt{2}}}\\
&=220.0~\mathrm{V}
\end{align}

(18)식에서와 같이 보통 220 V라고 말하는 가정용 전기의 전압은 교류신호의 실효값에 해당하는 표현임을 알 수 있어요.

마지막으로 본 글에서는 교류신호의 크기를 설명하기 위해 전압을 이용하여 설명드렸습니다만, 전류의 크기도 똑같이 적용하면 됩니다. 전류크기의 순간값, 최대값, P-P값, 평균값, 실효값도 모두 위에서 설명한 방식대로 똑같이 적용하면 됩니다.

\tag{19}
\begin{align}
&i=I_p \sin(\omega t)\\
&I_p\\
&I_{p-p} = 2I_p\\
&I_{avg} = 0.637 I_p\\
&I_{rms} = {{I_p}\over{\sqrt{2}}} 
\end{align}

Related posts.

정류회로 (rectification circuits) 자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 밀도 정의와 활용 사례 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요.