높이에 따른 위치에너지 변화

Last Updated on 2022-03-13 by BallPen

중력과 마찬가지로 높이에 따라 위치에너지도 변합니다. 위치에너지 공식을 함께 유도해 봐요.

높이에 따른 위치에너지 공식은 높이에 따른 중력과 중력가속도 변화 공식으로부터 유도됩니다.

과연 위치에너지는 높이(또는 고도)에 따라 어떻게 달라지고 공식은 어떻게 주어질까요? 과연 mgh가 나올까요?

함께 알아봐요.

다음은 이번 글의 목차입니다.

1. 높이에 따른 중력

이전 글에서 지구 표면으로부터 높이 x인 곳에 있는 물체에 작용하는 중력 F(x)는 다음과 같이 주어진다고 말씀드렸습니다.

\tag{1}
\begin{align}
F(x) &= ma\\
&= - m {{g{R_E}^2}\over{(R_E +x)^2}}
\end{align}

여기서 m은 지구 표면으로부터 높이 x에 있는 물체의 질량, a는 그 위치에서의 중력가속도, g는 지구 표면에서의 중력가속도 9.8~\mathrm{m/s^2}, R_E는 지구의 반지름입니다.

결국 물체에 작용하는 중력은 지구로부터 멀어질수록 x^2의 형태로 작아집니다.

2. 높이에 따른 위치에너지

2.1. 위치에너지 공식 유도

높이에 따른 위치에너지를 유도하기 위해서는 (1)식의 형태를 조금 바꾸어야 합니다.

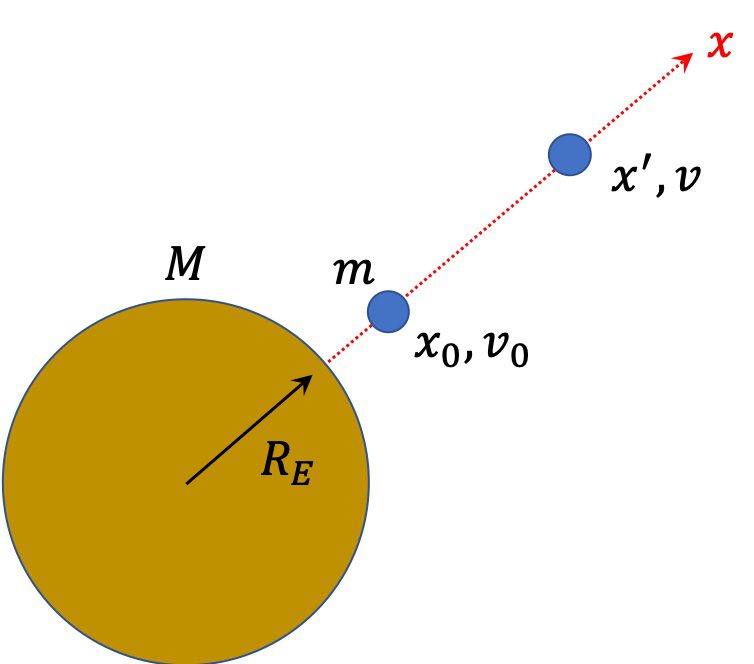
아래 [그림 1]은 지구 표면에서 질량 m인 어떤 물체를 던져올린 상황을 나타내고 있습니다. 물체가 위로 날아가면서 지구 표면으로부터 높이 x_0에서의 속도를 v_0, 높이 x ^\prime 에서의 속도를 v로 나타냅니다.

높이에 따른 위치에너지를 구하기 위해 (1)식에 주어진 가속도 a를 변형해보죠. 높이에 따라 가속도가 변하므로 가속도를 위치에 대한 표현으로 아래와 같이 변경할 수 있을거에요.

\tag{2}
\begin{align}
a&={{dv}\over{dt}}\\
&={{dv}\over{\red {dx}}}({{\red{dx}}\over{dt}})\\
&=v{{dv}\over{dx}}
\end{align}

식의 두번째 줄에서 dx를 나누어주고 곱해주었어요. 이러한 방식으로 식을 변형하는 것을 연쇄법칙이라 합니다.

(2)식의 가속도 a를 (1)식에 대입하면 아래와 같습니다.

\tag{3}
\begin{align}
ma = mv{{dv}\over{dx}}=-m{{g {R_E} ^2}\over{(R_E + x)^2}}\\
\end{align}

(3)식의 두번째 항과 세번째 항을 아래와 같이 변수 분리하고 양변을 적분합니다.

\tag{4}
\begin{align}
mvdv&=-mg{R_E}^2{{1}\over{(R_E + x)^2}} dx\\
m\int_{v_0}^v v dv &= -mg{R_E}^2 \int_{x_0}^x ({R_E}+x)^{-2} dx
\end{align}

편의상 (4)식의 좌변과 우변을 각각 나누어 계산하겠습니다.

먼저 (4)식의 좌변을 적분하면 아래와 같습니다.

\tag{5}
\begin{align}
m\int_{v_0}^v v dv &=m\Big[{{v^2}\over{2}}\Big]_{v_0}^v\\
&={{1}\over{2}}mv^2-{{1}\over{2}}m{v_0}^2
\end{align}

이번에는 (4)식의 우변을 적분하겠습니다. 이를 위해 적분기호 안에 있는 R_E + x를 k로 치환합니다. 그러면 x=k-R_E가 되고, {dx} \diagup {dk}=1입니다. 그러므로 dx=dk가 성립합니다.

\tag{6}
\begin{align}
-mg{R_E}^2 \int_{x_0}^x ({R_E}+x)^{-2} dx &=-mg{R_E}^2 \int_{x_0}^{x} k^{-2} dk\\
&=-mg{R_E}^2\Big[ {{k^{-1}}\over{-1}} \Big]_{x_0}^x\\
&=-mg{R_E}^2\Big[ -{{1}\over{k}} \Big]_{x_0}^x\\
&=-mg{R_E}^2 \Big[-{{1}\over{R_E + x}}\Big]_{x_0}^x\\
&=-mg{R_E}^2 \Big(-{{1}\over{R_E + x}}+{{1}\over{R_E + x_0}}\Big)\\
&=mg{R_E}^2 \Big({{1}\over{R_E + x}} - {{1}\over{R_E + x_0}}\Big)
\end{align}

이제 (5)식과 (6)식을 아래 (7)식처럼 서로 같게 놓으면 최종적으로 우리가 구하고자 하는 결과식이 도출됩니다.

\tag{7}
\begin{align}
{{1}\over{2}}mv^2 - {{1}\over{2}}m{v_0}^2 = mg{R_E}^2{{1}\over{R_E + x}}-mg{R_E}^2 {{1}\over{R_E + x_0}}
\end{align}

(7)식의 좌변은 우리가 흔히 알고 있는 운동에너지 변화량입니다. 그러므로 좌변은 에너지의 단위인 J을 갖습니다.

따라서 우변도 에너지의 단위인 J이 되어야 할 것입니다.

또한 우변의 각 항이 지구 표면으로부터의 위치 x에 의존하므로 위치에 의존하는 에너지라고 해서 중력 위치에너지( 또는 중력 포텐셜 에너지, potential energy)라고 부릅니다.

결국 우변도 x와 x_0에서의 위치에너지 변화량으로 볼 수 있습니다.

2.2. 무한대인곳에서의 위치에너지는 0

(7)식에 따르면 높이 x가 커질수록 위치에너지의 크기가 작아지게 됩니다. 그래서 x가 무한대인 곳에서의 위치에너지를 0으로 설정할 수 있어요.

이것이 타당한 이유는 여러분이 물체를 위로 던져 올리는 상황을 가정하면 이해할 수 있어요.

물체를 위로 던지면 얼마의 시간이 지난 후에 바닥으로 떨어질거에요. 만일 더 세게 던지면 그 물체는 더 높은 곳에 도달하게 되므로 바닥에 떨어지기까지 걸리는 시간이 길어집니다. 같은 방식으로 물체를 아주 더 세게 던지면 더욱 더 높은 곳에 도달하게 되죠. 그러면 바닥에 떨어지기까지의 시간은 더욱 길어집니다. 이러한 개념을 계속 연장해 보세요.

만일 정말 엄청나게 센 힘으로 던지면 물체는 아주 높은 곳까지 날라가게 되고요. 결국 바닥에 떨어지기까지의 시간이 무한대가 될거에요. 이말은 지구 표면으로부터 던져진 물체가 무한대까지 날아가면 다시는 지구로 떨어지지 못한다는 말이 됩니다.

그러므로 무한대인 지점에서의 위치에너지는 0으로 간주해야 하는 것입니다. 위치에너지가 0이므로 지구로 떨어지지 못하는 거에요.

2.3. 음의 부호를 갖는 위치에너지

결국 무한대인 곳의 위치에너지를 0으로 설정하면 무한대와 지구 사이에 있는 위치 x에서의 중력 위치에너지는 마이너스 부호를 가져야 합니다.

\tag{8}
\begin{align}
V(x) = -mg{R_E}^2 {{1}\over{R_E + x}}
\end{align}

따라서 마이너스 부호를 갖는 (8)식의 위치에너지 공식을 (7)식에 반영하면 다음과 같습니다.

\tag{9}
\begin{align}
{{1}\over{2}}mv^2 - {{1}\over{2}}m{v_0}^2 &=-\Big(-mg{R_E}^2{{1}\over{R_E + x}} \Big)+\Big(-mg{R_E}^2 {{1}\over{R_E + x_0}}\Big)\\
&= -{V(x)}+{V(x_0)}\\
\end{align}

(9)식을 더 정리하면 아래와 같이 유명한 역학적에너지보존 법칙이 유도됩니다.

\tag{10}
\begin{align}
{{1}\over{2}}mv^2 + V(x)={{1}\over{2}}m{v_0}^2 +{V(x_0)}
\end{align}

3. 높이에 따른 위치에너지 관련 예제

(문제) 지구 표면 x_0=0에서 수직 방향을 향해 초기 속력 v_0 = 140~\mathrm{m/s}로 질량 m=1~\mathrm{kg}인 어떤 물체가 던져졌다. 이 물체가 올라갈 수 있는 최고 높이 x는 얼마인가? 단 지구의 반지름 R_E = 6,400~\mathrm{km}이다.

(풀이) 이 문제를 풀기 위해서는 (10)식의 역학적 에너지보존 법칙을 적용하면 됩니다. 또한 물체는 최고 높이에서 나중 속력 v가 0이 됨을 기억하세요.

최고 높이 x에서의 위치에너지 V(x)를 먼저 구합니다.

\tag{11}
\begin{align}
V(x)&={{1}\over{2}}m{v_0}^2 +{V(x_0)} - {{1}\over{2}}mv^2\\
&={{1}\over{2}}m{v_0}^2 - mg{R_E}^2 {{1}\over{R_E + x}} - {{1}\over{2}}mv^2\\
&={{1}\over{2}} (1~\mathrm{kg}) ({140~\mathrm{m/s}})^2\\
&~~~~~~~-(1~\mathrm{kg})(9.8~\mathrm{m/s^2})(6400 \times10^3~\mathrm{m})^2 {{1}\over{6400\times10^3\mathrm{m}}+0}\\
&~~~~~~~-{{1}\over{2}}(1~\mathrm{kg})(0~\mathrm{m/s})^2\\
&=9800~\mathrm{J} - 62,720,000~\mathrm{J}-0~\mathrm{J}\\
&=-62,710,200~\mathrm{J}
\end{align}

그러므로

\tag{12}
\begin{align}
V(x)&=-62,710,200~\mathrm{J}\\
-mg{R_E}^2 {{1}\over{R_E + x}} &= -62,710,200~\mathrm{J}\\
-(1~\mathrm{kg})(9.8~\mathrm{m/s^2})(6400 \times10^3~\mathrm{m})^2 {{1}\over{6400\times10^3~\mathrm{m}}+x} &= -62,710,200~\mathrm{J}\\

\end{align}

(12)식으로부터 최고 도달 높이 x를 구하면 최종적으로 아래와 같습니다.

\tag{13}
\begin{align}
x \approx 1,000~\mathrm{m}
\end{align}

(8)식에 주어진 위치에너지 공식은 아주 정확한 표현식입니다. 그런데 (8)식 형태의 위치 에너지 공식 보다는 아마도 mgh가 더 친숙한 사람들이 많을 거에요. (8)식의 위치에너지 공식이 어떻게 mgh로 표현되는지 알고 싶으면 다음 링크를 클릭하세요. (중력위치에너지 공식이 mgh인 이유)

Related posts.

중력 위치에너지 공식이 mgh인 이유 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 속력과 속도 – 속력과 속도를 구분하는 이유와 차이 관성의 크기는 질량이 결정한다. 오차 – 계통오차, 과실오차, 우연오차의 개념과 예시 소음도 가산과 감산 연습 문제 벡터의 뺄셈 : 벡터의 변화량을 구하는 도구 각운동 – 각속도와 접선속도, 각가속도와 접선가속도의 관계