역학적 에너지 보존

Last Updated on 2023-05-25 by BallPen

역학적 에너지 보존 법칙을 유도하고 그 의미를 알아봅니다.

역학적 에너지 보존(Conservation of mechanical energy)이란 운동에너지(kinetic energy)와 위치에너지(potential energy)의 합이 위치와 무관하게 일정하게 유지되는 것을 말합니다.

수식으로 쓰면 다음과 같아요.

{1 \over 2} mv_0^2 + V(x_0) = {1 \over 2} {mv^2 + V(x)}

여기서 V(x_0)와 V(x)는 x_0와 x에서의 위치에너지를 뜻합니다.

이번 글에서는 역학적 에너지 보존 법칙이 어떠한 논리로 만들어지는지를 소개합니다. 아울러 위치에너지가 존재하기 위한 힘의 요건에 대해서도 이야기 합니다.

비록 개념은 단순하지만 의외로 생각할게 많은게 역학적 에너지 보존이에요.

이제부터 시작하겠습니다. 아래는 이번 글의 목차입니다.

1. 일과 운동에너지

역학적 에너지 보존 법칙이 성립하기 위해서는 위치와 연관된 어떤 힘이 있어야 합니다. 왜냐면 이 힘이 한 일이 운동에너지의 변화를 일으키기 때문이에요.

1-1. 위치와 연관된 힘

만일 어떤 힘 F가 x의 위치에 따라 변한다면 그 힘은 F(x)로 표기합니다. 이때 괄호안에 있는 x는 위치 x에 의존하여 힘의 크기가 결정됨을 뜻해요.

어떤 위치 x에 있는 질량 m인 물체에 힘 F(x)가 작용한다면 뉴턴 운동의 제2법칙에 따라 다음의 관계가 성립합니다.

\tag{1}
F(x) = ma = m {{dv}\over{dt}}

(1)식에서 a는 물체의 가속도로써 속도의 시간변화율 dv/dt로 주어집니다. 이것은 속도 v를 시간 t로 미분하는 개념이죠.

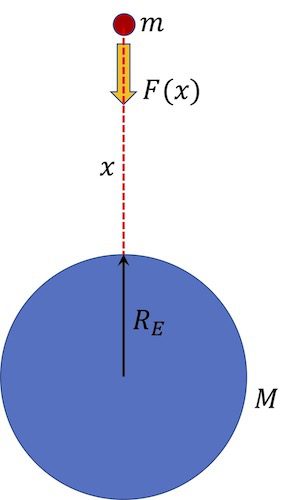
한편 아래 [그림 1]과 같이 지면으로부터 x만큼 높은 곳에 질량 m인 물체가 있다고 생각해봐요. 그러면 그 물체는 지구 중심쪽을 향해 만유인력을 받게 됩니다.

그러면 질량 m인 물체는 (1)식에 따라 가속도 a로 가속됩니다. 이때 물체에 작용하는 만유인력 F(x)의 크기는 다음과 같아요.

\tag{2}
F(x) = - G{{Mm}\over{(R_E + x)^2}}

여기서 G는 만유인력 상수로 G=6.67 \times 10^{-11}~\mathrm{N \cdot m^2 / kg^2}의 크기를 갖습니다. 또한 음의 부호는 작용하는 힘이 인력임을 뜻해요.

또한 중요한 것은 두 물체사이의 거리는 뉴턴의 구각 정리에 따라 각 물체 중심 사이의 거리로 계산해야 한다는 거에요. 그래서 두 물체사이의 거리가 (R_E + x)로 주어집니다.

(2)식에서 G,~M,~m,~R_E은 모두 상수에요. 그래서 값이 변하지 않아요. 하지만 x는 지구 표면으로부터의 위치 변수로서 물체에 작용하는 만유인력은 x에 의존하게 됩니다.

결국, (2)식은 위치와 연관된 힘입니다.

1-2. 위치와 연관된 힘이 한 일

그렇다면 위치와 연관된 힘 F(x)가 한 일을 구하면 어떤 결과가 얻어질까요?

(1)식에서부터 출발하겠습니다.

(1)식의 우변을 보면 속도를 시간으로 미분하는 형태로 가속도가 주어져 있어요. 이 식을 약간만 변형해야겠습니다. 아래 (3)식과 같이 미분의 연쇄 법칙을 적용하여 변형해 볼 께요.

\tag{3}
a = {dv \over dt} = {dv \over dx}\cdot{dx \over dt} = {dv \over dx}  \cdot v = v{{dv}\over{dx}}

한편 (3)식의 마지막 항은 아래 (4)식의 파랑색 항으로 바꾸어 표현해도 됩니다. 왜냐하면 그 결과가 서로 같기 때문이에요.

\tag{4}
{\color{blue}{1 \over 2} {{d(v^2)}\over{dx}}} = {1 \over 2} {{d(v^2)}\over{dv}} \cdot {{dv}\over{dx}} = {1 \over \cancel2} \cancel 2v {dv \over dx} = v{dv \over dx}

(3), (4)식을 반영하여 (1)식을 다시 정리해 볼 께요. 그러면 아래 (5)식과 같아요.

\tag{5}
\begin{align}
F(x) = ma &= m {{dv}\over{dt}}\\[10pt]
&=m\Big({1 \over 2} {{d(v^2)}\over{dx}}\Big)\\[10pt]
&={d \over dx} \Big({1\over 2} mv^2\Big)
\end{align}

그런데 식에서 (1/2)mv^2 이 나오는데요. 우리는 이것을 보통 기호 T로 표기하고 운동에너지라고 불러요.

운동에너지를 반영해서 (5)식을 다시 쓰면 다음과 같아요.

\tag{6}
F(x) = {d \over dx} \Big( {1 \over 2 }{mv^2} \Big) = {d T\over dx}

이렇게 하고 났더니 위치와 연관된 힘 F(x)가 한 일을 쉽게 구할 수 있을 것 같아요. (6)식의 좌변과 우변에 dx를 곱하면 다음과 같이 일에 대한 식으로 바꿀 수 있어요.

\tag{7}
F(x) dx = dT

이제 (7)식을 적분합니다. 이때 위치는 x_0에서 x까지, 운동에너지는 T_0에서 T까지로 하겠습니다.

\tag{8}
\begin{align}
W=\int_{x_0}^{x} F(x)dx &= \int_{T_0}^{T}dT \\[10pt]
&= T-T_0 \\
&= {1\over 2 }{}mv^2  - {1 \over 2} mv_0^2
\end{align}

이것은 초기 높이 x_0에서 나중 높이 x까지 물체가 낙하하는 동안 힘 F(x)가 한 일 W에 대응합니다.

중요한 것은 이 힘이 한 일이 운동에너지의 변화량으로 주어진다는 거에요.

즉, 어떤 물체에 힘 F(x)가 일은 하면 그 물체의 운동에너지가 변한다는 의미입니다. 바꾸어 말하면 운동에너지 변화를 이끌어내기 위해서는 그 물체에 일을 해주어야 한다는 말과 같아요.

일과 운동에너지 사이의 관련을 나타내는 (8)식을 일과 운동에너지 정리하고 부릅니다. 일과 운동에너지 정리란 어떤 물체에 일을 해주면 그 물체의 운동에너지가 해준 일만큼 변한다는 의미입니다.

2. 보존력이 만드는 위치에너지

2-1. 위치에너지

(8)식에 따르면 위치와 연관된 힘 F(x)가 물체에 한 일 W만큼 운동에너지가 변합니다.

예를 들어 위치와 연관된 힘이 물체에 일을 함으로써 그 물체의 운동에너지가 증가했다면, 반대로 힘이 물체에 일을 하는 동안 운동에너지와는 다른 형태의 어떤 에너지는 감소되어야 한다고 정의할 수 있을거에요.

그 근거는 에너지 보존 법칙입니다. 이 법칙에 따르면 에너지의 형태는 바뀔 수 있지만 그 총 양은 항상 일정하게 유지된다는 거에요.

즉, 힘이 한 일에 의해 운동에너지가 증가했다면 다른 형태의 에너지는 그 만큼 감소한다고 보는 거에요. 이 가정에 따라 다음 (9)식의 관계를 만들 수 있을거에요.

\tag{9}
F(x)dx = -dV(x)

(7)식에 따르면 F(x)dx가 운동에너지 변화량 dT를 만들므로, 동일한 F(x)dx는 V(x)라고 표기된 에너지도 변화시키는 개념입니다. 이때 운동에너지 T와 어떤 에너지 V는 한쪽이 증가하면 다른 한쪽은 감소해야 하므로 (9)식에 음의 부호가 붙어 있어요.

이 식에서 V(x)는 위치와 연관된 어떠한 에너지인데요. 우리는 이 에너지를 위치에너지(potential energy)라고 부릅니다.

따라서 힘이 일을 하는 동안 운동에너지가 증가한다면 위치에너지는 감소해야 하고, 운동에너지가 감소하면 위치에너지는 증가합니다.

이때 힘이 한 일이 항상 위치에너지를 만들어내는 것은 아닙니다. 보존력이 일을 하는 경우에만 위치에너지를 정의할 수 있고, 비보존력이 일을 하는 경우에는 위치에너지를 정의할 수 없음을 참고하기 바랍니다.

이번에도 (9)식의 양변을 적분합니다. 그러면 다음과 같아요.

\tag{10}
\begin{align}
W = \int_{x_0}^{x} F(x)dx &= - \int_{V_{(x_0)}}^{V(x)}V(x)\\[11 pt]
&=-V(x) +V(x_0)
\end{align}

2-2. 위치에너지의 몇 가지 사례

(10)식에서 위치에너지를 V(x)로 표기했는데요. 이것은 위치에너지가 위치 x에 의존하여 그 크기가 결정됨을 뜻합니다.

위치에너지가 정의되는 몇가지 사례를 잠깐 소개합니다.

첫번째 사례는 중력에 의한 위치에너지입니다. 그 수식은 다음과 같습니다.

\tag{E-1}
\begin{align}
V(x) = - mg {R_E} ^2 {{1}\over{R_E + x}}
\end{align}

위치에너지가 위치 x에 의존함을 알 수 있어요.

한편 지구 표면 근처의 높이 h인 곳에서의 위치에너지로 한정한다면 (E-1)식은 다음과 같이 근사적으로 바꾸어 쓸 수 있어요.(공식변환과정)

\tag{E-2}
V(h) = mgh

두번째 사례는 용수철에 의한 탄성위치에너지입니다. 용수철이 평형위치로부터 x만큼 압축되거나 늘어나면 용수철 내부에 위치에너지가 저장됩니다. 그 크기를 식으로 나타내면 다음과 같아요.

\tag{E-3}
V(x) = {1 \over 2} kx^2

이 식에서 k는 용수철이 갖는 탄성의 척도인 용수철 상수입니다.

3. 역학적 에너지 보존 법칙

이제 마지막으로 정리만 하면 역학적 에너지 보존 법칙을 만들어 낼 수 있어요.

(8)식과 (10)식의 좌변은 서로 동일하게 힘이 한 일을 의미합니다. 그러므로 (8)식과 (10)식의 우변도 서로 같아야 해요.

결국 (8)식의 우변과 (10)식의 우변을 서로 같다고 놓으면 다음 식이 성립합니다.

\tag{11}
\begin{align}
{1 \over 2} mv^2 - {1 \over 2} mv_0^2 = -V(x) + V(x_0)
\end{align}

(11)식을 x와 x_0위치에서의 운동에너지와 위치에너지의 합으로 표현하면 다음과 같습니다.

\tag{12}
{1 \over 2} mv_0^2 + V(x_0) = {1 \over 2} {mv^2 + V(x)}

우리는 (12)식을 역학적 에너지 보존 법칙이라 부릅니다.

4. 역학적 에너지 보존 법칙 예제 풀이

관련 예제를 하나만 풀어봐요.

(예제) 정지상태에 있던 어떤 물체를 자유낙하시켰다. 이 물체가 최초의 위치로부터 15 m 낙하했을 때의 운동에너지는 10 m 낙하했을 때의 운동에너지에 비하여 몇 배가 되겠는가? 단, 공기 저항력은 무시한다.

(풀이) 보존력인 중력이 작용하는 공간에서 자유낙하하는 물체에 대한 문제입니다. 이 문제는 15 m 낙하했을 때의 역학적 에너지와 10 m 낙하했을 때의 역학적 에너지가 서로 같다는 보존 법칙을 이용하면 됩니다.

\tag{E-4}
\begin{align}
15~ \mathrm m ~지점의~ 역학적~ 에너지 = 10~\mathrm{m} ~지점의 ~역학적~에너지
\end{align}

이를 식으로 쓰면 다음과 같습니다.

\tag{E-5}
\begin{align}
{1 \over 2} mv^2 +  \color{red}mgh \color{black}= {1 \over 2}  m {v^{\prime}}^2 +  mgh^{\prime} 

\end{align}

여기서 v는 15 m 낙하 지점에서의 물체의 속도입니다. 그리고 물체가 바닥까지 떨어지는 높이를 15 m라고 가정한다면 h는 0 m 가 됩니다. 그래서 (E-5)식의 빨강색 항은 0이 됩니다.

이때 주의할 것은 h는 물체가 떨어진 거리가 아니고 바닥으로부터의 높이라는 것을 명심해야 해요.

동일한 방식으로 v^{\prime}은 10 m 지점을 통과할 때 물체의 속도입니다. 그리고 h^{\prime}은 최초의 위치로부터 10 m 낙하하였으므로 전체높이 15 m에서 10 m를 뺀 5 m가 됩니다.

일단 (E-5)식을 더 정리해보겠습니다.

15 m 떨어진 지점의 운동에너지와 10 m 떨어진 지점의 운동에너지 비율을 구하기 위해 (E-5)식의 양변을 {( 1/2 )} {mv^{\prime}}^2로 나누어 봐요.

그러면 아래와 같습니다.

\tag{E-6}
\begin{align}
{{{1 \over 2}mv^2}\over{{1 \over 2} {mv^{\prime}}^2}} = 1 + {{mgh^{\prime} } \over {{1}\over{2}}{mv^{\prime}}^2}
\end{align}

윗 식을 간단히 하기 위해 질량 m을 서로 약분해봐요. 그러면 식은 다음과 같이 변형됩니다.

\tag{E-7}
\begin{align}
{{{1 \over 2}v^2}\over{{1 \over 2} {v^{\prime}}^2}} &= 1 + {{gh^{\prime} } \over {{1}\over{2}}{v^{\prime}}^2}\\
\end{align}

한편 윗 식의 우변에서 나머지 요소들은 모두 그 값을 알고 있는데 분모에 있는 v^{\prime}은 아직 모르고 있어요. 따라서 이 값을 구해야만 해요.

이 값을 구하기 위해서는 자유낙하에 대한 등가속도 운동방정식을 활용하면 됩니다.

\tag{E-8}
\begin{align}
{v^{\prime}}^2 &= {v_0}^2 + 2g\Delta x\\
&=0~\mathrm{m^2 / s^2} + (2\times 9.8\mathrm {m/s^2} \times 10~\mathrm{m})  \\
&=196~\mathrm{ m^2 / s^2}
\end{align}

여기서 v_0는 물체의 초기속도인데요 최초 정지해 있었으므로 0 m/s가 됩니다. 그리고 \Delta x는 물체가 떨어진 거리로서 10 m 입니다. g는 지구표면에서의 중력가속도입니다.

(E-8)의 결과를 (E-7)에 대입하고 정리하면 아래와 같습니다.

\tag{E-9}
\begin{align}
{{{1 \over 2}v^2}\over{{1 \over 2} {v^{\prime}}^2}} &= 1 + {{gh^{\prime} } \over {{1}\over{2}}{v^{\prime}}^2}\\[10pt]
&=1 + {{9.8 ~\mathrm{m/s^2}\times 5~\mathrm{m}}\over{{1}\over{2}}\times196~\mathrm{m^2 / s^2} }\\[10pt]
&=1 + {{49}\over{98}}\\[10pt]
&=1+{1 \over 2}\\[10pt]
&={3 \over 2}

\end{align}

결국 물체가 15 m 낙하한 지점에서의 운동에너지는 10 m 낙하한 지점에서의 운동에너지보다 1.5배 큽니다.

Related posts.

높이에 따른 위치에너지 변화 중력 위치에너지 공식이 mgh인 이유 자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 풍량과 풍량효율 측정 및 계산법이 궁금한가요 단위 – SI 단위, 10의 거듭제곱, 접두어 및 올바른 단위 표기법 SEM 이론 – (1) 주사전자현미경과 관련된 기초 물리학 이론 조명 – 단색광, 다색광, 복사선속, 광선속, 광도, 조도, 휘도의 완벽 정리 유효 숫자 계산 예제