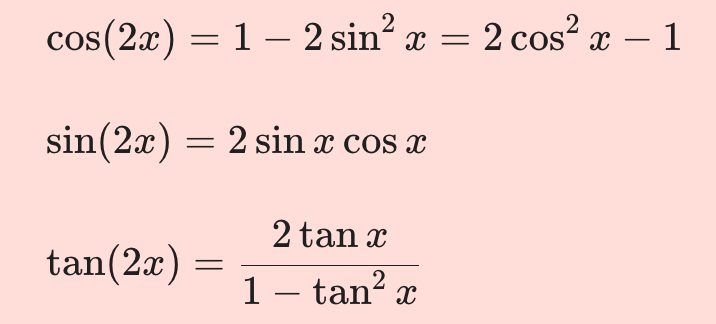Last Updated on 2024-01-06 by BallPen
삼각함수 항등식 중 두배각 공식을 알아보겠습니다.
이번 글에서는 삼각함수 두배각 공식(double angle formulas)을 알아보겠습니다.
여기서 두배각이란 어떤 각도를 x라 할 때 그 두 배인 (x+x)가 되어 (2x)가 된다는 의미에요.
즉 \sin (2x), \cos (2x), \tan (2x)가 어떻게 표현되느냐 하는 것입니다.
결론부터 말씀드리면 다음과 같아요.
\tag{D1}
\begin{align}
&\sin (2x) = 2 \sin x \cos x\\[10pt]
&\cos (2x) = 1-2 \sin^2 x=2 \cos^2 x -1\\[10pt]
&\tan (2x) = {{2 \tan x}\over{1- \tan^2 x}}
\end{align}위 (D1)식의 두배각 공식들이 각각 어떻게 유도되는지는 아래를 참고하세요.
1. 사인 두배각 공식
sine 두배각 공식의 유도과정 입니다. 삼각함수의 합차 공식을 적용하면 됩니다.
\tag{1}
\begin{align}
\sin(2x)&=\sin(x+x)\\
&=\sin x \cos x + \cos x \sin x\\
&=2\sin x \cos x
\end{align}2. 코사인 두배각 공식
이번에는 cosine 두배각 공식입니다. 삼각함수의 합차 공식과 \sin^2 x + \cos^2 x = 1 의 관계를 적용하면 됩니다.
\tag{2}
\begin{align}
\cos(2x) &= \cos(x+x)\\
&=\cos x \cos x - \sin x \sin x\\
&=\cos^2 x - \sin^2 x\\
&=(1-\sin^2 x) - \sin^2 x\\
&=1-2 \sin^2 x
\end{align}한편 위 (2)식의 세번째 줄에 \sin^2 x + \cos^2 x = 1 의 관계를 \sin^2 x에 적용하면 아래(3)식도 성립합니다.
\tag{3}
\begin{align}
\cos(2x) &= \cos(x+x)\\
&=\cos x \cos x - \sin x \sin x\\
&=\cos^2 x - \sin^2 x\\
&=\cos^2 x - (1-\cos^2 x)\\
&=2 \cos^2 x -1
\end{align}3. 탄젠트 두배각 공식
계속 이어서 tangent 두배각 공식도 유도해봐요.
그런데 공식을 유도하는 과정중에 1 / (\cos^2 x)의 관계가 필요해서 이것을 먼저 구하겠습니다.
[공식 유도에 필요한 관계식]
\tan x = \sin x / \cos x입니다. 이를 제곱해서 정리하면 다음과 같아요.
\tag{4}
\begin{align}
&\tan^2 x = {{\sin^2 x}\over{\cos^2 x}} = {{1 - \cos^2 x}\over{\cos^2 x}} = {{1}\over{\cos^2 x}} - 1\\[10pt]
&{{1}\over{\cos^2 x}} = \tan^2 x + 1
\end{align}[탄젠트 두배각 공식 유도]
(4)식 두번째 줄의 관계를 이용해 탄젠트 두배각 공식을 구해보면 아래 (5)식과 같아요.
\tag{5}
\begin{align}
\tan(2x) &= {{\sin(x+x)}\over{\cos(x+x)}}\\[10pt]
&={{2\sin x \cos x}\over{1-2 \sin^2 x}}\\[10pt]
&={{{2 \sin x \cos x}\over{\cos ^2 x}}\over{{1- 2 \sin^2 x}\over{\cos^2 x}}}\\[10pt]
&={{2 \tan x}\over{{{1}\over{\cos^2 x}}-2 \tan^2 x}}\\[10pt]
&={{2 \tan x}\over{\tan^2x + 1 - 2 \tan^2x}}\\[10pt]
&={{2 \tan x}\over{1-\tan^2 x}}
\end{align}위 식의 첫번째 줄에 (1)식과 (2)식을 적용한 것이 두번째 줄입니다. 그리고 두번째 줄에서 분자와 분모를 공통적으로 \cos^2x로 나누면 세번째 줄이 됩니다. 그리고 네번째 줄의 분모에 1/{\cos^2 x}가 있는데요. (4)식의 두번째 줄을 그곳에 대입하면 됩니다.
3 thoughts on “두배각 공식”