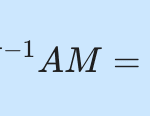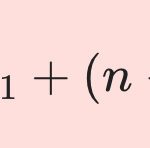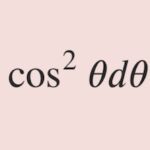로피탈의 정리

Last Updated on 2025-03-25 by BallPen

로피탈의 정리를 알아보고 그 의미를 그래프로 확인해 봐요.

로피탈의 정리(l’Hospital’s rule)를 알아보고 예제를 풀어볼 거에요.

그리고 매스매티카로 각 예제에 대한 그래프를 그려 로피탈의 정리가 뜻하는 개념을 구체적으로 이해해 봐요. 혹시 관심있는 분이 있다면 그래프를 따라서 그려보시라고 본문에 매스매티카 코드도 함께 제시합니다.

로피탈의 정리에 대한 증명은 위키백과를 참고하시기 바랍니다. 아래는 이번 글의 목차에요.

1. 로피탈의 정리

로피탈의 정리는 두 함수 f(x)와 g(x)가 x=a가 포함된 구간에서 미분가능할 때,

또는

의 조건하에서, 아래 식과 같이 두 함수를 미분하고 나눈 극한 값이 $L$이라면,

다음 관계가 성립한다는 정리입니다. 이때 $g^{\prime }(x) \ne 0$입니다.

2. 로피탈의 정리 예제

로피탈의 정리를 적용한 예제 2개를 풀어 봐요.

2-1. 예제 1

다음 식의 극한 값을 구해보세요.

문제에 주어진 식의 분자와 분모에 있는 두 함수에 대해 $x \rightarrow 0$일 때의 극한값을 구해보면 다음과 같이 (1-1)식을 만족합니다.

그리고 두 함수를 각각 미분한 다음에 극한값을 구해 봐요. 그 결과는 다음과 같습니다.

극한 값이 1로 도출되었으므로 로피탈의 정리 (1-4)식에 의해 다음 관계가 성립합니다.

결국 문제에서 주어진 식의 극한 값은 1입니다.

[그래프로 확인해 보기]

아래 그래프는 예제에 주어진 분수식의 분자 $\sin x$와 분모 $x$를 각각 그래프로 나타낸 거에요.

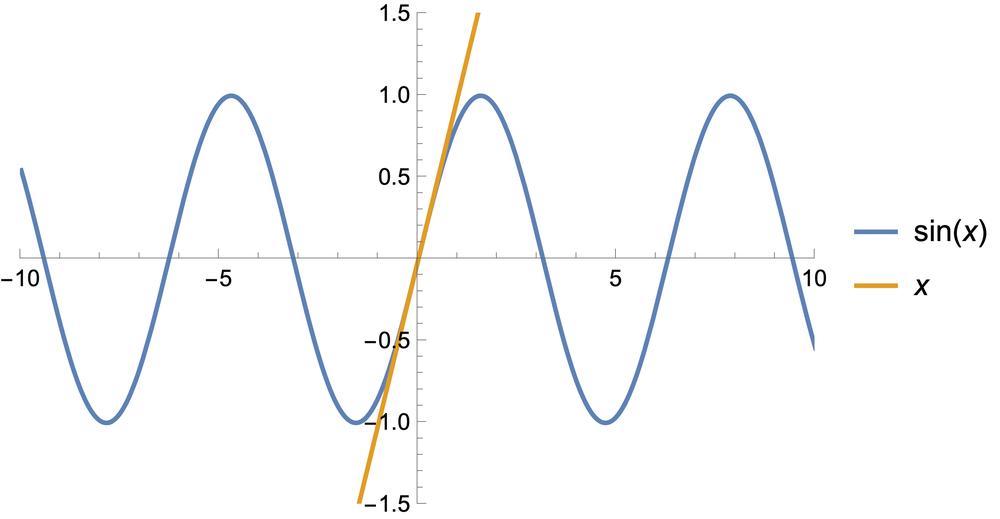
그림처럼 $x \rightarrow 0$에서 두 함수는 모두 0으로 수렴하고 있어요. 즉, 이것은 (2-2)식의 조건이 분명하게 성립한다는 것을 의미해요.

이 조건하에서 (2-4)식, 즉 로피탈의 정리가 성립하는지 알아보기 위해 ${{\sin x}\over{x}}$와 $\cos x$의 그래프를 그려볼게요.

그 결과가 다음 그림입니다.

그림과 같이 (2-2)식이 성립하는 $x \rightarrow 0$에서만이 극한 값이 1로 서로 같다는 것을 알 수 있어요.

정말 로피탈의 정리가 옳다는 것을 알 수 있어요. 아주 신기해요.

예제를 하나만 더 풀어 봐요.

2-2. 예제 2

다음 식의 극한 값을 구해보세요.

우선 로피탈의 정리를 적용하기 위한 전제 조건이 성립되는지 알아보기 위해 $x \rightarrow \infty$에서 분자와 분모에 있는 두 함수의 극한 값을 각각 구해 봐요.

그 결과 (1-2)식의 조건을 만족하는 것을 알 수 있어요.

이번에는 두 함수를 각각 미분한 다음에 극한을 구해 볼께요.

극한 값이 0으로 도출되었으므로 로피탈의 정리 (1-4)식에 의해 다음 관계가 성립합니다.

결국 문제에 주어진 식의 극한은 0입니다.

[그래프로 확인해 보기]

아래 그래프는 예제에 주어진 식의 분자 $\ln x$와 분모 $x$를 각각 그래프로 그려본 거에요.

그림처럼 $x \rightarrow \infty$에서 두 함수는 모두 $\infty$로 수렴해가는 것을 알 수 있어요. (2-6)식의 조건이 성립한다는 것을 의미합니다.

이 조건하에서 (2-7)식의 로피탈의 정리가 성립되는지 확인하기 위해 ${{\ln x}\over{x}}$와 $1 \over x$의 그래프를 함께 그려볼게요.

어떤가요? $x \rightarrow \infty$에서 두 함수의 극한 값이 0으로 서로 같게 될 것임을 짐작할 수 있어요.

로피탈의 정리가 분명히 성립하는 군요.