리액턴스(reactance)

Last Updated on 2024-06-13 by BallPen

전기용량 리액턴스와 유도 리액턴스 공식을 유도하고 그 의미를 알아봐요.

리액턴스(reactance)는 교류전원에 축전기나 인덕터(또는 ‘코일’, ‘솔레노이드’, ‘유도기’라 불림)가 연결될 때 나타나는 저항의 성질(또는 반응저항)을 말해요.

축전기에서 발생하는 리액턴스 X_c를 ‘전기용량 리액턴스’ 또는 ‘용량성 리액턴스’라 부르고, 인덕터에서 발생하는 리액턴스 X_L를 ‘유도 리액턴스’ 또는 ‘유도성 리액턴스’라고 해요.

각각의 공식은 다음과 같이 주어지고, 저항의 단위인 \Omega을 사용합니다.

\tag{D1}
\begin{align}
X_c = {1 \over{2 \pi f C}}\\[15pt]
X_L = 2 \pi f L
\end{align}

윗 식에서 f는 교류전원의 진동수, C는 축전기의 전기용량(capacitance), L는 인덕터의 유도계수(inductance)에요.

그럼 이제부터 (D1)과 (D2)식을 유도해보고 그 의미를 알아보겠습니다.

아래는 이번 글의 목차에요.

이 글에서 활용한 그림자료는 아래에서 다운받을 수 있어요. 키노트 파일이 원본 그림파일이고 파워포인트는 변환된거에요. 그래서 파워포인트 파일은 그림 일부가 깨져 보일 수도 있어요. 아울러 매스매티카 작업파일도 pdf로 함께 올려드립니다.

맥 키노트 파일 : reactance.key

파워포인트 파일: reactance.pptx

매스매티카 노트북 파일: reactance.pdf

1. 교류회로에서의 저항

리액턴스를 시작하기 전에 교류회로에서의 저항과 옴의 법칙을 간단히 알아봐요.

아래 [그림 1]은 저항 R이 교류전원과 연결된 것을 나타내고 있습니다.

그림과 같이 저항에 걸린 순간전압 v_R이 다음과 같이 사인꼴로 진동한다고 생각해봐요.

\tag{1-1}
v_R = V_p  \sin \omega t

여기서 V_p는 교류전원의 최대전압, \omega는 교류전원의 각진동수, t는 시간이에요.

이때 저항을 통과하는 순간전류 i는 다음과 같이 옴의 법칙을 적용하면 구할 수 있어요.

\tag{1-2}
\begin{align}
i &= {v_R \over {R}}\\[10pt]
&={{V_p \sin\omega t}\over{R}}\\[10pt]
&={V_p \over R} \sin\omega t
\end{align}

그런데 위 (1-2)식의 마지막줄에서 V_p와 R은 모두 상수이므로, {V_p}\over{R}도 상수에요. 그래서 이것을 I_p로 표기하고 최대전류라고 부르기로 해요.

\tag{1-3}
I_p = {{V_p}\over{R}}

그러면 저항을 통과하는 전류 (1-2)식은 다음과 같이 표현될거에요.

\tag{1-4}
i = I_p \sin \omega t

(1-1)식과 (1-4)식을 통해 저항에 걸린 전압과 저항을 통과하는 전류는 모두 동일한 진동수 \omega로 진동하는 것을 알 수 있어요.

다만, (1-3)식에 따라 최대 전류 I_p는 저항 R이 커질수록 점점 작아집니다.

[저항에 걸린 전압과 전류 그래프]

지금까지 저항이 교류전원과 연결되었을 때 저항에 걸린 전압과 저항을 통과하는 전류에 대해 알아봤어요.

만일 저항값을 R=2~\Omega, , 교류전원의 최대 전압을 V_p = 6~\rm V, 교류전원의 각진동수를 \omega = 2~\rm rad/s라 할 때 (1-1), (1-4)식에 따라 저항에 걸린 순간전압과 순간전류는 아래와 같이 주어집니다.

\tag {1-5}
\begin{align}
v_R &= V_p \sin \omega t =  6 \sin 2 t\\[10pt]
i &= I_p \sin \omega t = 3 \sin 2 t
\end{align}

이때 (1-5)식에 대한 전압과 전류 그래프를 매스매티카(mathematica)로 그려보면 다음과 같아요.

그래프로부터 전압 곡선의 최대 전압이 6 V이고, 전류곡선의 최대 전류는 3 A임을 알 수 있어요. 그리고 전압이 최대일 때 전류도 최대, 전압이 0일 때 전류도 0으로 나타나 두 곡선의 위상이 서로 같다는 것을 알 수 있습니다.

2. 교류회로에서의 축전기와 인덕터

이제부터 이 글의 목적인 리액턴스를 알아봐요.

리액턴스는 축전기나 인덕터가 교류전원에 연결되었을 때 나타나는 저항의 성질을 말합니다. 반대로 말하면 직류회로에서는 리액턴스는 나타나지 않아요.

먼저 축전기에 의한 전기용량 리액턴스부터 알아봐요.

1-1. 전기용량 리액턴스

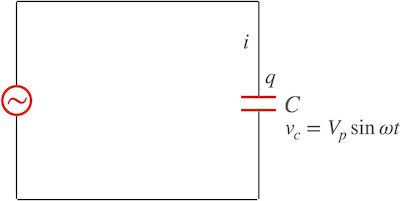
아래 [그림 3]은 교류전원에 전기용량 C인 축전기가 연결된 모습이에요.

그림에 표기한 것처럼 축전기 양단에 걸린 교류 순간전압이 아래와 같다고 생각해봐요.

\tag{2-1}
v_c = V_p \sin \omega t

그렇다면 축전기를 통과하는 순간 전류 i는 어떻게 될까요? 회로를 보면 저항이 없으므로 옴의 법칙에 의해 회로를 통과하는 전류는 무한대가 될 것 같아요.

그런데 정말 무한대로 전류가 흐를까요?

축전기 양단의 전압이 (2-1)식처럼 변한다는 것은 축전기에 저장된 전하량이 사인꼴 모양으로 충전과 방전한다는 의미에요. 어느 순간 t에서 축전기에 저장된 전하량을 q라고 해봐요. 그러면 순간전하량 q는 다음의 축전기 공식을 통해 구할 수 있어요.

\tag{2-2}
q=Cv_c

이때 (2-2)식을 시간으로 미분해봐요. 그러면 전류 정의식을 통해 축전기를 통과하는 순간전류 i를 구할 수 있게 됩니다.

\tag{2-3}
\begin{align}
i={dq \over dt} &= {{dCv_c}\over{dt}}\\[10pt]
&=C{{dv_c}\over{dt}}\\[10pt]
&=C{d \over dt}(V_p \sin \omega t)\\[10pt]
&=\omega CV_p \cos \omega t
\end{align}

여기서도 상수끼리의 곱은 또 다른 상수일 뿐이므로 치환해봐요. 즉 \omega, C, V_p는 모두 초기에 주어진 상수이므로, \omega C V_p를 최대 전류 I_p로 치환하겠습니다.

\tag{2-4}
I_p = \omega C V_p

또한 (2-3)식의 마지막 줄에 주어진 \cos \omega t는 삼각함수의 덧셈 정리에 따라 \sin(\omega t + {{\pi}\over{2}})와 같아요.

\tag{2-5}
\begin{align}
\sin(\omega t + {\pi \over 2}) &= \sin \omega t \cos {\pi \over 2} + \cos \omega t \sin{\pi \over 2}\\[10pt]
&=\cos \omega t
\end{align}

그러므로 (2-3)식의 가장 마지막 줄을 다시 정리하면 축전기를 통과하는 교류 순간 전류를 아래 (2-6)식처럼 쓸수 있어요.

\tag{2-6}
i = I_p \sin(\omega t + {\pi \over 2})

한편 (2-4)식을 통해 축전기를 통과하는 최대 전류 I_p를 정의했는데요. 이 식을 옴의 법칙 I={{V}\over{R}}의 형태로 바꾸어 봐요. 그러면 다음과 같다는 것을 알 수 있어요.

\tag{2-7}
\begin{align}
I_p = {{V_p}\over{1/{\omega C}}}
\end{align}

그러면 결국 윗 식의 분모에 있는 1/{\omega C}이 저항의 역할을 해야 한다는 것을 알 수 있어요.

이것은 아주 중요한 개념으로 [그림 3]의 회로에는 어떠한 저항도 존재하지 않지만 축전기가 교류 회로에 놓이게 되면 1/{\omega C}의 저항이 생긴다는 의미에요.

그래서 통상의 저항 R과 구분하기 위해 X_c라 표기하고, 명칭도 ‘전기용량 리액턴스’로 정하게 되었어요.

결국 전기용량 리액턴스는 아래 (2-8)식과 같이 주어집니다. 단위는 저항과 동일하게 \Omega입니다.

\tag{2-8}
\begin{align}
X_c = {1 \over {\omega C}} = {{1}\over{2 \pi f C}}
\end{align}

여기서 \omega = 2 \pi f의 관계가 활용되었어요.

다시 말씀드리면 전기용량 리액턴스는 축전기가 교류전원과 연결될 때 나타나는 저항의 성질입니다. 이것이 재미있는 것은 통상의 저항 R은 전원 진동수와 무관하게 일정하지만, 전기용량 리액턴스는 (2-8)식처럼 전원의 진동수 f에 의존하여 달라집니다.

축전기의 전기용량이 0.2~\rm F인 경우, 교류전원의 진동수에 따른 전기용량 리액턴스는 다음과 같이 변해요.

전기용량 리액턴스 X_c는 교류전원의 진동수 f가 커질수록 점점 작아지는 것을 알 수 있어요. 즉, 전류가 더 잘 통해요.

[축전기에 걸린 전압과 전류 그래프]

참고로 축전기에 걸린 순간 전압과 순간 전류는 (2-1)식과 (2-6)식으로 주어진다고 말씀드렸어요.

만일 축전기의 전기용량이 C=0.2~\rm F, 교류전원의 최대 전압을 V_p = 6~\rm V, 교류전원의 각진동수를 \omega = 2~\rm rad/s라 할 때 (2-1), (2-6)식은 다음과 같이 표현될 거에요.

\tag{2-9}
\begin{align}
v_c &= V_p \sin \omega t = 6 \sin 2 t\\[10pt]
i &= (2 \times0.2\times 6) \sin(2t + {{\pi} \over {2}})=2.4\sin(2t + {\pi \over 2})
\end{align}

그리고 그래프를 그려보면 아래와 같습니다.

여기서 중요한 것은 축전기에 걸린 전압이 최대일때 흐르는 전류는 0이고, 전압이 0일 때 전류는 최대라는 거에요. 즉 저항의 경우에는 전압과 전류의 위상이 동일한데, 축전기는 전압과 전류의 위상이 \pi \over 2만큼 어긋납니다.

1-2. 유도 리액턴스

아래 [그림 6]은 교류전원에 유도계수 L인 인덕터가 연결된 모습이에요.

이번에는 그림에 표기한 것처럼 인덕터를 통과하는 교류 순간전류가 아래와 같다고 생각해봐요.

\tag{2-10}
i = I_p \sin \omega t

그리고 인덕터에 걸린 순간전압 v_L을 함께 구해 봐요.

인덕터에 걸린 전압은 인덕터를 통과하는 전류의 시간변화율에 비례하는데요. 이때 비례상수가 유도계수 L에요. 식으로 표현하면 다음과 같습니다.

\tag{2-11}
\begin{align}
v_L &= L {{di}\over{dt}}\\
\end{align}

윗 식에 (2-10)식을 대입하고 정리해 보세요. 그러면 다음과 같습니다.

\tag{2-12}
\begin{align}
v_L &= L {{d}\over{dt}} (I_p \sin \omega t)\\[10pt]
&= \omega L I_p \cos \omega t\\[10pt]
&=\omega L I_p \sin(\omega t + {{\pi}\over{2}})

\end{align}

위 식에서도 (2-5)식의 관계를 활용해서 \cos을 \sin으로 바꾸었습니다.

한편 식에서 \omega, L, I_p는 모두 상수이므로, \omega L I_p를 최대 전압 V_p로 치환해봐요.

\tag{2-13}
V_p = \omega L I_p

그러면 (2-12)식의 가장 마지막 줄을 정리하면 인덕터에 걸린 순간 전압은 아래 식으로 주어집니다.

\tag{2-14}
v_L = V_p \sin(\omega t + {{\pi}\over{2}})

한편 (2-13)식을 통해 V_p를 정의했는데요. 이 식을 옴의 법칙 형태로 바꿔보면 다음과 같아요.

\tag{2-15}
\begin{align}
I_p = {{V_p}\over{\omega L}}
\end{align}

그러면 위 식의 분모에 있는 \omega L이 저항의 역할을 해야 한다는 것을 알 수 있어요.

[그림 6]에서도 분명히 저항이 없는데요. 인덕터가 교류 회로에 놓이게 되면 \omega L의 저항이 생긴다는 의미입니다.

그래서 통상의 저항 R, 전기용량 리액턴스 X_c와 구분하기 위해 X_L로 표기하고, 명칭을 ‘유도 리액턴스’로 정하게 되었어요.

결국 유도 리액턴스는 아래 식과 같이 주어집니다. 단위는 저항과 동일하게 \Omega입니다.

\tag{2-16}
X_L = \omega L = 2 \pi f L

유도 리액턴스도 전기용량 리액턴스와 유사하게 교류전원의 진동수 f에 의존하는데요. 다만 이 경우에는 서로 비례 관계를 갖습니다.

유도계수가 0.2~\rm H인 경우에 대해 이 관계를 그래프로 그려보면 다음과 같아요.

유도 리액턴스 X_L은 교류 전원의 진동수 f가 커질수록 점점 커지는 것을 알 수 있어요. 즉 전류가 잘 흐르지 못해요.

[인덕터에 걸린 전압과 전류 그래프]

만일 인덕터의 유도계수가 C=0.2~\rm H, 인덕터를 통과하는 최대 전류를 I_p = 6~\rm A, 교류전원의 각진동수를 \omega = 2~\rm rad/s라 할 때 (2-10), (2-14)식은 다음과 같이 표현될 거에요.

\tag{2-17}
\begin{align}
v_L &= (2 \times 0.2 \times 6) \sin(\omega t + {\pi \over 2}) = 2.4 \sin (\omega t + {\pi \over 2})\\[10pt]
i &= I_p \sin \omega t = 6 \sin 2 t
\end{align}

그리고 그래프를 그려보면 아래와 같습니다.

여기서 중요한 것은 인덕터에 걸린 전압이 최대일 때 인덕터를 흐르는 전류는 0이고, 전압이 0일 때 전류는 최대라는 거에요. 즉 축전기와 유사하게 인덕터가 교류전원에 있게 되면 전압과 전류는 {{\pi}\over{2}}만큼 위상이 어긋납니다.

이상으로 전기용량 리액턴스와 유도 리액턴스 공식을 유도하고 그 의미를 알아봤습니다. 전기용량 리액턴스는 교류전원의 진동수와 반비례하고, 유도 리액턴스는 진동수와 비례합니다. 아울러 저항에 걸린 전압과 흐르는 전류는 위상이 동일하지만, 축전기와 인덕터의 경우에는 전압과 전류가 {{\pi}\over{2}}만큼 어긋나 있음을 꼭 기억하세요.

Related posts.

자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 밀도 정의와 활용 사례 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요. 선풍기 살 때 풍량 효율 큰 것 고르면 되는 거에요?