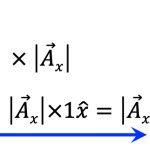벡터의 덧셈 : 기하학적 표현과 수학적 처리

Last Updated on 2021-11-18 by BallPen

벡터를 합한다는 것은 기하학 및 수학적으로 어떻게 표현하고 처리할 수 있을까요?

벡터의 덧셈 에 대한 기하학적 표현과 수학적 처리 방법을 설명드립니다.

혹시 벡터와 관련하여 다른 내용이 궁금하시면 아래의 추천 글 목록을 참고하세요.

• 벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분 (클릭)
• 단위벡터 의미와 벡터 정규화 (클릭)
• 벡터의 방향 표기를 정확하게 하는 방법 (클릭)
• 벡터의 덧셈 : 기하학적 표현과 수학적 처리
• 벡터의 뺄셈 : 벡터의 변화량을 구하는 도구 (클릭)

아래는 이번 글의 목차입니다.

1. 물체에 하나의 힘 벡터가 작용할 때

벡터량에는 여러가지 물리량이 있습니다. 속도, 가속도, 힘, 운동량 등이 이에 해당하는데요. 이중에서 우리가 가장 이해하기 쉬운 것이 힘 벡터일것입니다.

어느 물체에 힘 벡터가 작용할 때 그 물체의 운동 특성을 우선 알아보겠습니다.

아래의 사진을 보아 주세요. 파이프가 실려있는 바지선이 견인선(tug boat)에 이끌려 이동되고 있습니다. 이때 앞에 있는 견인선은 바지선을 잡아 끄는 힘 \vec{F}을 제공하고 있습니다. 이 힘은 질량이 m인 바지선에 작용되는 것이죠.

[그림 1] 견인선이 바지선을 끌고 가고 있습니다. (이미지 출처: Tug boat and pipes” by Phil_Parker is licensed under CC BY 2.0)

만일 바지선에 작용하는 모든 마찰력을 무시한다면 이 상황을 그림으로 아래와 같이 나타낼 수 있습니다. 또한 뉴턴 운동의 제2법칙에 따라 물체의 운동방정식은 (1)식과 같습니다.

[그림 2] 질량이 m인 물체에 힘 \vec{F_1}이 x방향으로 작용하고 있습니다.

\tag{1}
\begin{align}
\vec{F}_1 = F_{1x} \hat{x} = m\vec{a}
\end{align}

따라서 바지선은 견인선이 제공하는 힘에 의해 아래의 (2)식과 같이 가속도를 갖게 됩니다. 또한 가속도의 방향은 힘의 방향과 동일하게 x방향을 향합니다.

\tag{2}
\vec{a} = {{F_{1x}}\over{m}} \hat{x} 

2. 벡터의 덧셈 : 물체에 2개 이상의 힘 벡터가 작용할 때

벡터를 더하기 위해서는 2개 이상의 동일한 종류의 벡터가 있어야 합니다.

여기에서도 힘 벡터들을 생각해 보겠습니다. 아래 사진을 보세요.

이 사진에는 커다란 군함이 있는데요. 이 군함은 지금 스스로의 동력으로 움직이고 있지 않습니다. 줄로 연결되어 있는 견인선들이 이 군함을 끌고 있어요.

이와 같이 하나의 물체에 2개 이상의 힘이 작용하는 경우 이들 힘에 대한 벡터 합의 방향으로 물체는 움직이게 됩니다. 그렇다면 두개 이상의 벡터가 작용할 때 그 합 벡터를 어떻게 구할 수 있을까요?

[그림 3] 실생활 속 벡터의 덧셈이 필요한 순간. 견인선에 의한 두개 이상의 힘이 로프에 의해 군함에 작용하고 있습니다. 벡터 합의 방향과 크기에 따라 군함은 움직이게 됩니다. (이미지 출처: “USS Mount Whitney is escorted by tug boats as it pulls into the Viktor Lenac dry dock.” by Official U.S. Navy Imagery is licensed under CC BY 2.0)

2-1. 벡터의 덧셈 : 기하학적 표현

단순한 예를 들어 보겠습니다.

아래 [그림 4]는 질량 m인 어느 물체에 두 힘이 작용하고 있는 것을 위에서 본 그림입니다. 그림과 같이 x방향과 y방향으로 두 힘이 동시에 작용하고 있는데요.

힘이 하나뿐인 경우에는 힘이 작용하는 방향으로 그 물체는 가속됩니다. 그런데 2개의 힘이 작용할 때는 두 힘의 알짜힘은 어느 방향을 향할까요? 또 알짜 힘의 크기는 어떻게 주어질까요?

[그림 4] x방향과 y방향으로 두 힘이 작용하고 있습니다. 이러한 상황에서 물체에 작용하는 알짜 힘의 크기와 방향은 어떻게 될까요?

알짜힘의 크기와 방향을 구하기 위해서는 두 힘 \vec{F_1}과 \vec{F_2}를 합해야 합니다. 그런데 어떻게 해야 합하는 걸까요?

그래서 예전 사람들은 이 상황에 대해 수많은 실험을 했어요. [그림 4]와 같이 두 힘이 작용할 때 물체는 어느 방향으로 이동하고 그때 작용하는 알짜힘의 크기를 구해본거에요. 이때 알짜 힘의 방향은 물체가 움직이는 방향을 뜻하고, 알짜힘의 크기는 (3)식에서와 같이 가속도를 구하면 알짜힘의 크기를 구할 수 있어요.

그 결과 두개 이상의 힘이 한 물체에 작용할 때 합의 합성법이 정립되었답니다.

아래 [그림 5]는 [그림 4]에서 주어진 두 힘의 합에 대한 기하학적 절차를 나타냅니다. 여기서 주목할 것은 이러한 합성의 방법과 동일하게 자연 현상이 실제로 벌어진다는 거에요. 자연에 이러한 현상이 존재하기 때문에 벡터의 합을 이러한 방식으로 구하는 것으로 이해하시면 좋습니다.

[그림 5] 벡터의 덧셈. 두 힘을 합한다는 것은 첫번째 벡터의 머리에 두번째 벡터의 꼬리를 평행이동하여 붙인 후, 첫번째 벡터의 꼬리와 두번째 벡터의 머리를 잇는 벡터가 두 벡터의 합 벡터입니다.

벡터를 합한다는 것은 [그림 5]와 같이 첫번째 벡터 \vec{F_1}의 머리에 두번째 벡터 \vec{F_2}를 오른쪽으로 평행 이동하여 꼬리에 붙입니다. 그 다음에 \vec{F_1}의 꼬리에서 시작하여 \vec{F_2}의 머리를 향하는 벡터를 그렸을 때 그것이 두 벡터의 합벡터 \vec{F}=\vec{F_1} + \vec{F_2}입니다.

벡터의 덧셈을 처음 접할 때 이러한 합성 방법이 매우 어색해요. 왜 이렇게 해야 하는지 잘 이해가 안가죠. 하지만 위에서 말씀드렸듯이 자연이 이러한 규칙을 따르기 때문에 벡터 합의 절차를 이렇게 정했다고 생각하시면 편합니다.

[그림 5]에서 제시한 벡터합은 F_1에 F_2를 더했는데요, 아래 [그림 6]과 같이 F_2에 F_1을 더해도 결과는 같게 나옵니다.

이러한 특성을 벡터 합의 교환법칙이라고 합니다.

[그림 6] 벡터의 덧셈 순서를 달리해도 벡터 합의 결과는 달라지지 않습니다. 이 그림에서의 벡터 합의 결과는 [그림 5]의 결과와 동일한 크기와 방향을 갖습니다.

결국 2개 이상의 벡터가 있을 때 각 벡터의 크기와 방향을 알고 있다면 [그림 5] 또는 [그림 6]의 방법대로 각각의 벡터를 작도합니다. 그 다음에는 합 벡터를 그리세요. 그리고 합 벡터의 길이와 각도를 자와 콤파스로 측정하면 크기와 방향을 구할 수 있습니다.

2-2. 벡터의 덧셈 : 수학적 처리

작도법을 이용하면 기하학적으로 합 벡터의 크기와 방향을 쉽게 구할 수 있어요. 그러나 아주 엄밀한 결과를 얻기 위해서는 작도 방법으로는 어렵습니다. 그래서 수학적으로 벡터를 합하는 방법이 필요해요.

이에 대한 공식을 만들기 위해 다음과 같은 상황을 생각해보세요.

아래의 [그림 7]에도 \vec{F}_1과 \vec{F}_2가 한 물체에 작용하고 있습니다. 이때 \vec{F}_1은 가로축 방향성분만 가지므로 F_{1y}는 일단 0이 됨을 알 수 있습니다.

우선 기하학적으로 두 벡터를 합해보겠습니다.

[그림 7] 두 힘 벡터가 한 물체에 동시에 작용하고 있습니다. 그렇다면 이 물체는 어느 방향으로 가속운동을 하게 될까요? 이를 알기 위해서는 벡터의 덧셈 연산을 해야 합니다.

그러면 아래 [그림 8]과 같이 작도할 수 있어요. 빨강색 벡터 \vec{F}_1에 노랑색 벡터 \vec{F}_2를 합했습니다. 그리고 빨강색 벡터의 꼬리에서 노랑색 벡터의 머리를 향해 합벡터 F를 그렸어요.

제대로 잘 한거에요. 틀리지 않았습니다.

그런데 여기서 조금만 더 생각을 해봐요. 아래 [그림 8]과 같이 노랑색 벡터를 x성분과 y성분벡터로 분해하여 그릴 수 있을 거에요. 그러면 F_{2x}\hat{x}와 F_{2y}\hat{y}벡터가 그려지게 됩니다.

이것을 ‘벡터를 성분분해했다”라고 말하는데요.

[그림 8] 벡터는 x방향과 y방향으로 분해될 수 있습니다. 벡터를 합한다는 것은 x방향끼리 합하고 y방향끼리 합하면 됩니다.

합 벡터는 성분분해된 벡터끼리의 합으로도 표현이 가능합니다. [그림 8]에서 x방향으로 2개의 성분벡터가 있어요. 그리고 y방향으로는 하나의 성분벡터가 있습니다.

그리고 수학적으로 각 방향의 성분끼리 더하는거에요. 바로 아래 (3)식 처럼요

\tag{3}
\begin{align}
\vec{F} &=\vec{F}_1 + \vec{F}_2\\
&= F_{1x}\hat{x} + (F_{2x}\hat{x} + F_{2y}\hat{y})\\
&=(F_{1x} + F_{2x})\hat{x} + F_{2y}\hat{y} 
\end{align}

이와 같이 벡터를 합한다는 것은 수학적으로는 x방향의 모든 벡터 성분을 합하고, y방향의 모든 벡터 성분을 합하는 절차를 거치면 됩니다.

[예제] 벡터의 합

아래 [그림 9]와 같이 한 물체에 두 힘이 작용하고 있다. (1) 이 물체에 작용하는 알짜 힘을 구하여라. (2) 알짜 힘의 방향을 구하여라. (3) 알짜 힘의 단위 벡터를 구하여라.

[그림 9] 벡터의 덧셈 예제 상황. 두 힘이 한 물체에 작용하고 있습니다. 이 물체에 작용하는 알짜 힘을 구하고 그 방향을 구해보세요.

(1) 알짜힘 구하기

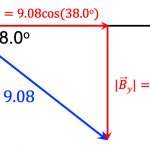
문제에서 주어진 두 힘 벡터를 성분별로 분해하여 그림으로 나타내면 아래 [그림 10]과 같다.

[그림 10] 벡터의 덧셈을 연산하기 위한 벡터의 성분 분해

물체에 작용하는 알짜 힘인 합 벡터는 다음과 같이 구한다.

\tag{4}
\begin{align}
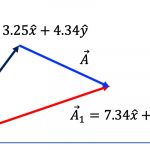
\vec{F} &= \vec{F}_1 + \vec{F}_2\\
&=(8.17\hat{x}-2.19\hat{y}) + (9.81\hat{x}+4.37\hat{y})\\
&=(8.17+ 9.81)\hat{x} + (-2.19+4.37)\hat{y}\\
&=17.98\hat{x} + 2.18\hat{y}
\end{align}

(2) 알짜 힘의 방향 구하기

알짜 힘은 (4)식에 주어져 있습니다. 알짜힘의 방향은 아래와 같이 구하면 됩니다.

\tag{5}
\begin{align}
\tan\theta &= {{F_y}\over{F_x}}\\
&={{2.18}\over{17.98}}\\
&=0.121\\
\theta &=\tan^{-1} 0.121 \\
&=6.90^\circ
\end{align}

(3) 알짜 힘의 단위벡터 구하기

벡터 정규화를 통해 알짜 힘의 단위벡터를 구할 수 있습니다. 우선 알짜 힘의 크기를 구하면 아래 (6)식과 같습니다.

\tag{6}
\begin{align}
|\vec{F}| &= \sqrt{{F_x}^2 + {F_y}^2}\\
&=\sqrt{{17.98}^2 + {2.18}^2}\\
&=18.1
\end{align}

벡터 정규화를 하면 단위벡터가 나옵니다.

\tag{7}
\begin{align}
단위벡터 &= {{\vec{F}}\over{|\vec{F}|}}\\
&={{17.98\hat{x} + 2.18\hat{y}}\over{18.1}}\\
&=0.99\hat{x} + 0.12\hat{y}
\end{align}

3. 벡터의 덧셈 요약

• 벡터를 더한 다는 것은 2개 이상의 벡터가 한 물체에 작용하는 경우에 알짜 벡터를 구하는 과정으로 볼 수 있다.
• 벡터의 덧셈은 처음 벡터의 머리에 나중 벡터의 꼬리를 붙인 후, 처음 벡터의 꼬리에서 나중 벡터의 머리를 연결하는 벡터를 그려 기하학적으로 표현할 수 있다.
• 수학적으로는 벡터를 x성분과 y성분으로 분해하고 같은 방향성분끼리 더하면 된다.

Related posts.

벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분 단위벡터 의미와 벡터 정규화 벡터의 방향 표기를 정확하게 하는 방법 벡터의 뺄셈 : 벡터의 변화량을 구하는 도구 벡터의 실수배 : 벡터에 스칼라를 곱하는 방법과 기하학적 의미 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요. 전자기파 스펙트럼 대역의 구분, 특징과 활용 네이비즘 서버 시간 알림 사이트를 보고 떠오른 옛 추억과 표준 시간의 중요성