Last Updated on 2025-08-27 by BallPen
산술 평균, 기하 평균, 조화 평균이란 무엇이고 실생활에서 사용되는 사례를 살펴보겠습니다.
평균 값을 산출하는 공식의 종류에는 산술, 기하, 조화 평균이 있습니다. 대체적으로 많은 사람들이 활용하고 있는 것이 산술 평균입니다.
산술 평균은 어느 값들을 대표하는 하나의 값을 산출하기 위해 많이 사용되고 있는데요. 그렇다면 기하 평균과 조화 평균의 개념은 무엇이고 언제 사용하는 걸까요?
산술, 기하, 조화 평균의 개념을 서로 비교하고 실생활에서의 사용 사례를 알아보겠습니다.
목차는 다음과 같습니다.
1. 산술평균
1-1. 정의
실생활에서 평균이라고 말하면 보통 산술 평균을 의미합니다. 산술 평균은 데이터 값 x_i들을 모두 합한 후에 데이터의 갯수 n으로 나눈 값입니다.
\tag{1} \bar x = {{\sum x_i}\over{n}}데이터 값들의 대표값을 산출할 때 주로 사용하는 기법입니다. 이 기법은 데이터 분포가 종 모양으로 중앙 근처에서 많이 분포하고 양끝단에서 작아지는 유형에 적합합니다. 이 경우 평균값은 중앙 근처에 위치하는 값으로 나오게 되죠.
그러나 주변에서 많이 산술 평균을 사용하다보니 항상 이 평균값이 데이터가 산출된 집단의 중심에 위치하는 값을 가리키는 것으로 간혹 착각하기도 합니다.
사실 산술 평균은 데이터의 양쪽 극단치에 의해 아주 민감하게 영향을 받습니다. 극단치란 다른 데이터와 비교하여 극단적으로 크거나 작은 값을 말합니다.
그러므로 데이터에 극단치가 존재하는 경우 산술 평균을 대표 값으로 사용하기에는 부적당합니다. 이러한 산술 평균의 함정을 피하기 위해 중앙값이나 최빈값이 대표 값으로 대신하여 산출되기도 합니다.
1-2. 실생활 활용 사례
200만원의 월급을 받는 사람이 5명이고 2 000만원의 월급을 받는 사람이 1명이라고 할 때 산술 평균 \bar x을 구해 보겠습니다.
\tag{2}
\begin{aligned}
\bar x &= {{x_1 +\ldots + x_n}\over{n}} \\
&= {{200만원+\ldots+2~000만원}\over{6}} \\
&=500 만원
\end{aligned}그 결과 (2)식에서와 같이 산술 평균은 500만원으로 계산되었습니다. 이것은 통계적으로 사람 1인당 500만원의 월급을 받는다는 의미입니다.
(참고) 만일 다른 집단의 평균이 250만원일 경우, 이 집단의 평균값 500만원은 아주 큰 수치입니다. 이를 근거로 이 집단의 올해 임금 인상을 동결한다고 하면 매우 억울할 것입니다.
왜냐면 6명중 5명은 단지 200만원을 받을 뿐인데 한 사람이 받는 고액 월급 때문에 평균값이 높게 나왔기 때문입니다. 이러한 경우 한 사람이 받는 2 000만원의 숫자가 극단치에 해당합니다.
이러한 경우가 산술 평균을 집단의 대표 값으로 사용하기에 부적당한 하나의 사례에 해당합니다. 따라서 산술 평균을 대할 때에는 극단치가 포함되어 있는지의 여부를 알아보는 것이 중요합니다.
2. 기하평균
2-1. 정의
인구증가율, 물가상승율, 경제성장률 등과 같이 연속적인 변화율 데이터를 기반으로 어느 구간에서의 평균 변화율을 구할 때 사용하는 것이 기하평균입니다.
이 기하평균은 변화율에 대한 데이터 값 x_i들을 모두 곱한 후에 데이터의 갯수로 n제곱근을 취한 값입니다.
\tag{3}
\begin{aligned}
G &= \sqrt[n]{\Pi_{i=1}^{n}{x_i}}\\
&= (x_1\times \ldots \times x_n)^{1/n}
\end{aligned}간혹 기하평균은 (3)식의 양변에 자연로그(natural logarithm)를 취해 아래의 (4)식처럼 변형해 사용하기도 합니다.
\tag{4}
\begin{aligned}
\ln G &= {{1}\over{n}} \ln{(x_1 \times \ldots \times x_n)}\\
&={{1}\over{n}}(\ln{x_1} + \ldots + \ln{x_n})\\
&= {{1}\over{n}} \sum_{i=1}^{n} \ln x_i\\
G &=\exp\big({{{1}\over{n}} \sum_{i=1}^{n} \ln x_i} \big)
\end{aligned}2-2. 실생활 활용 사례
이미 설명한 바와 같이 기하 평균은 변화율들의 평균변화율을 구할 때 사용합니다.
아래 이미지는 지난 1년간의 달러-원(USD/KRW) 환율의 변화를 나타냅니다. 2020년 10월 2일에서 2021년 10월 2일까지의 평균변화율을 어떻게 구할수 있을까요? 유사한 예제를 보겠습니다.
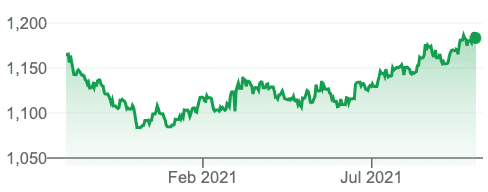
최근 3개월간 달러/원(USD/KRW) 환율이 매달 10%, 80%, -5.0% 변화했다고 가정하겠습니다(단순 가정입니다. 심각해지지 마세요). 3개월간의 평균 환율 증가율은 얼마일까요? 단, 3개월 전의 달러단 원화의 환율은 1000원으로 간주하겠습니다.
이것을 그림으로 표현하면 아래와 같습니다.
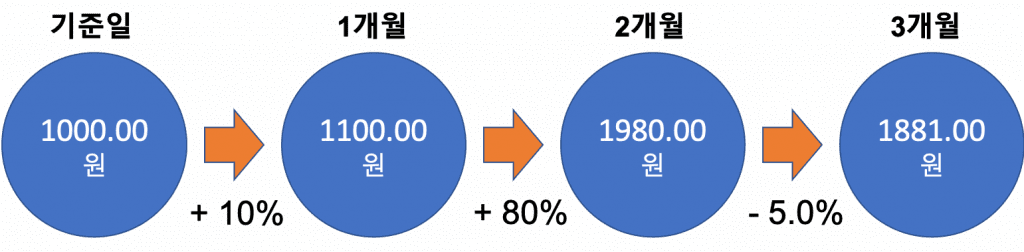
그렇다면 3개월 동안의 평균 증가율은 얼마일까요?
혹시 산술평균으로 3개월간의 평균 환율 증가율을 구하면 될것 같다고 생각하셨나요? 결과는 ‘그러시면 안됩니다‘ 입니다.
\tag{5}
\begin{aligned}
\bar x &= {{10\% + 80\%-5.0\%}\over{3}}\\
&=28.3\%
\end{aligned}(5)식과 같이 산술평균으로 구하면 28.3%라는 그럴듯한 수치가 얻어집니다. 이 수치를 이용해 기준일의 환율이 3개월 동안 어떻게 달라지는지 아래 그림으로 알려드립니다. 만일 산술 평균이 옳다면 3개월 후에는 1881.00원이 나와야 하겠죠.
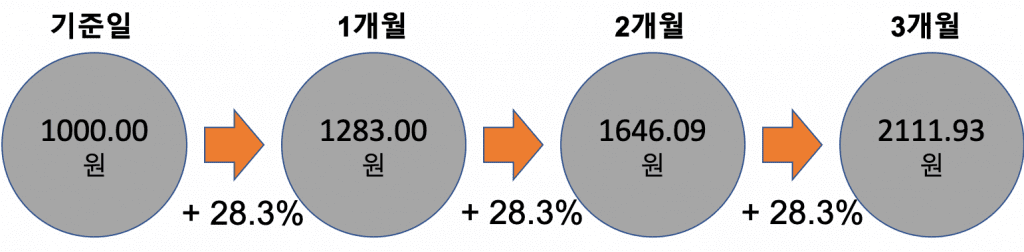
결과는 1881.00원이 아니라 2111.93원이 나와 230.93원의 절대오차가 발생되었습니다. 이것은 산술평균을 적용하여 평균증가율을 계산하는 것이 잘못되었기 때문입니다.
그렇다며 이번에는 (3)식의 기하평균으로 구하고 그 값을 통해 매 월마다의 변화를 그림으로 나타내겠습니다.
\tag{6}
\begin{aligned}
G &= (x_1 \times \ldots \times x_n)^{1/n}\\
&=(1.10 \times 1.80 \times 0.95)^{1/3}\\
&=1.234\\
&=23.4\%
\end{aligned}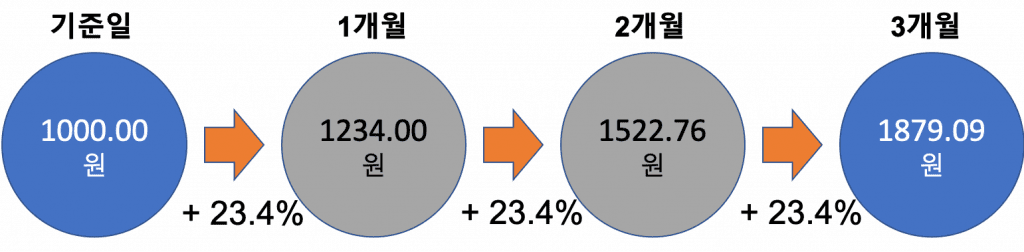
그 결과 평균변화율은 23.4%가 나왔으며, 이를 통해 계산해보면 3개월 후에는 1879.09가 나오게 됩니다. 이 값은 소수점 처리에 의한 오차를 감안할 때 원래의 값인 1881.00원과 거의 동일한 값으로 간주할 수 있습니다.
결국 변화율들에 대한 평균변화율은 산술 평균이 아닌 기하 평균으로 구해야 되는 것을 알 수 있습니다.
3. 조화평균
3-1. 정의
조화 평균은 평균속력을 구할 때 사용하게 됩니다. 아래 (7)식과 같이 각각의 데이터 값의 역수를 취하여 산술 평균을 구한 후 다시 역수를 취한 값이 조화 평균입니다.
\tag{7}
\begin{aligned}
H &= {{1}\over{{1}\over{n}} {\sum {{1}\over{x_i}}}}\\
&= {{1}\over{{1}\over{n}}({{1}\over{x_1}}+\ldots+{{1}\over{x_n}})}
\end{aligned}3-2. 실생활 활용 사례
아래 그림의 A지점에서 B 지점까지의 거리는 12 km입니다. 그리고 A지점에 비해 B지점의 고도가 더 높다고 생각해보겠습니다.
이때 누군가가 자전거를 타고 A에서 B로 이동할 때 평균 속력이 v_1 = 6 km/h이고, 반대로 B에서 A로 이동할 때 v_2 = 12 km/h로 이동했다고 해보겠습니다.
이것을 그림으로 표현하면 아래와 같습니다.
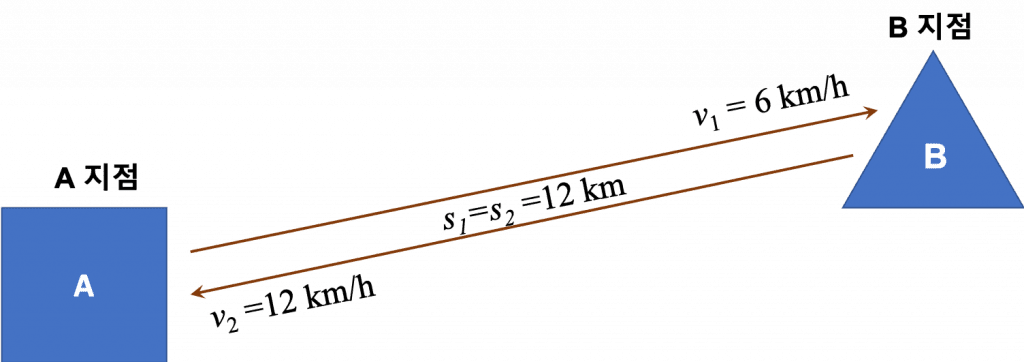
그렇다면 A \rightarrow B \rightarrow A로 이루어지는 왕복 경로 동안 자전거가 이동하는 동안의 평균 속력은 얼마일까요?
혹시 산술평균으로 왕복하는 동안의 평균속력을 구하면 될것 같다고 생각하셨나요? 결과는 ‘그러시면 안됩니다‘ 입니다.
\tag{8}
\begin{aligned}
\bar x &= {{6 ~\mathrm{km/h} + 12~\mathrm{km/h}}\over{2}}\\
&=9 ~\mathrm{km/h}
\end{aligned}(8)식과 같이 산술평균으로 구하면 9 km/h라는 수치가 얻어집니다. 이 수치를 이용하면 왕복하는 동안의 경과시간이 그대로 나올까요?
우선 자전거가 왕복하는데 걸리는 시간은 아래의 (9)와 (10)식의 합으로부터 총 3 h이 됩니다.
- A에서 B로 이동할 때 걸리는 시간
\tag{9}
\begin{aligned}
t_1 &= {{s_1}\over{v_1}}\\
&= {{12 ~\mathrm{km}}\over{6~\mathrm{km/h}}}\\
&=2~\mathrm{h}
\end{aligned} - B에서 A로 이동할 때 걸리는 시간
\tag{10}
\begin{aligned}
t_1 &= {{s_2}\over{v_2}}\\
&= {{12 ~\mathrm{km}}\over{12~\mathrm{km/h}}}\\
&=1~\mathrm{h}
\end{aligned} 이번에는 산술 평균으로 구한 평균 속력 \bar x = 9 km/h를 적용하여 왕복 s=24 km를 이동하는데 걸리는 총 시간 t를 구하겠습니다. 만일 이 값이 제대로 된 평균 속력이 맞다면 총 3 h이 똑같이 도출되어야 합니다.
\tag{11}
\begin{aligned}
t &= {{s}\over{\bar x}}\\
&= {{24~\mathrm{km}}\over{9~\mathrm{km/h}}}\\
&=2.7~ \mathrm{h}
\end{aligned}그러나 (11)식과 같이 값을 구해보면 2.7 h이 나와 산술 평균으로 구한 평균속력이 틀렸음을 나타냅니다.
그렇다면 이번에는 (7)식의 조화 평균으로 평균속력을 구해보겠습니다.
\tag{12}
\begin{aligned}
H &= {{1}\over{{1}\over{n}}({{1}\over{x_1}}+\ldots+{{1}\over{x_n}})}\\
&={{1}\over{{1}\over{2}}({{1}\over{6~\mathrm{km/h}}}+{{1}\over{12~\mathrm{km/h}}})}\\
&=8~\mathrm{km/h}
\end{aligned}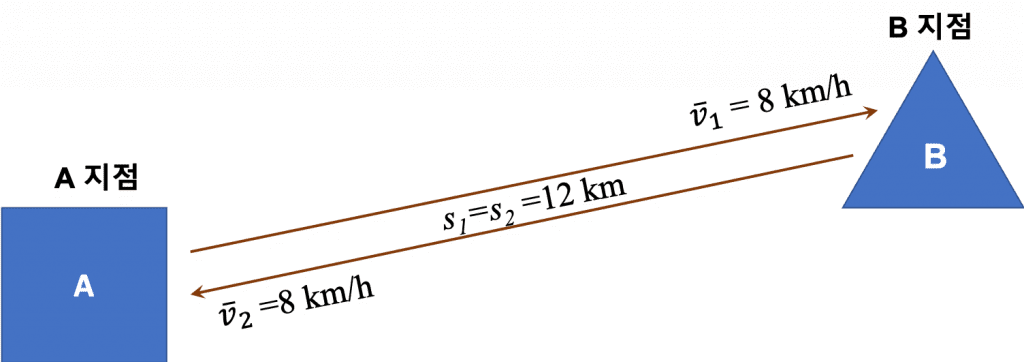
그 결과 조화 평균 값은 8 km/h가 나왔으며, 이를 통해 왕복하는데 걸리는 시간을 계산해보면 아래의 (13)식과 같이 총 3 h이 나옵니다.
\tag{13}
\begin{aligned}
t &= {{s}\over{\bar v}}\\
&={{24~\mathrm{km}}\over{8~\mathrm{km/h}}}\\
&=3~\mathrm{h}
\end{aligned}결국 구간별 속력 값으로부터 전체의 평균속력을 구하기 위해서는 산술 평균이 아닌 조화 평균으로 구해야 되는 것을 알 수 있습니다.
산술, 기하, 조화 평균 정리
- 산술평균은 데이터 값들을 모두 합한 후에 데이터의 갯수로 나누어 구한다. 극단치가 없는 경우에는 대표값으로 사용하기에 적당하나 극단치가 있는 경우에는 데이터의 특성을 나타내는 대표값으로 사용하기에 적절치 못하다.
- 기하평균은 변화율에 대한 데이터 값들을 모두 곱한 후에 데이터의 갯수로 제곱근을 취하여 구한다. 구간별 변화율 데이터로부터 전체 구간에 대한 평균 변화율을 구할 때 사용할 수 있다.
- 조화평균은 구간별 데이터 값의 역수를 취하여 산술 평균을 구한 후에 다시 역수를 취하여 구한다. 구간별 평균속력 데이터로부터 전체 구간에 대한 평균속력을 구할 때 사용할 수 있다.


큰 도움 됐습니다.
감사합니다.
방문해주셔서 감사합니다.
예제를 들어서 설명 해 주시니 정확히 이해하게 되었습니다.
큰 도움이 되었습니다. 감사 합니다.
방문해 주셔서 감사합니다.
액셀 함수 공부하다가 우연히 들르게 되었는데 평균의 세 가지 개념을 재미있게 풀어서 설명해놓으셨네요. 재미있게 잘 보았습니다
방문해주셔서 감사합니다.^^