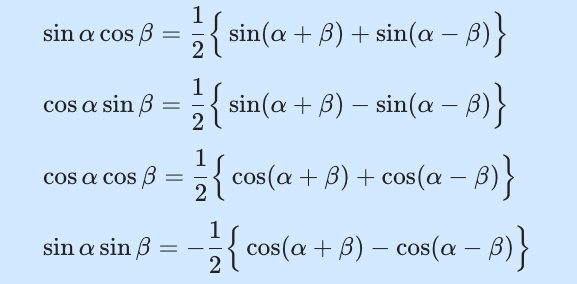삼각함수 곱을 합으로 바꾸는 공식 : 곱셈 공식

by

Last Updated on 2024-12-11 by BallPen

삼각함수 곱을 합 또는 차로 바꾸는 곱셈 공식을 유도해봐요.

삼각함수 곱을 합으로 바꾸는 곱셈 공식입니다.

sin⁡αcos⁡β=12{sin⁡(α+β)+sin⁡(α−β)}cos⁡αsin⁡β=12{sin⁡(α+β)−sin⁡(α−β)}cos⁡αcos⁡β=12{cos⁡(α+β)+cos⁡(α−β)}sin⁡αsin⁡β=−12{cos⁡(α+β)−cos⁡(α−β)}\begin{align*} &\sin\alpha \cos \beta = {1 \over 2} \Big\{ \sin(\alpha + \beta) + \sin (\alpha - \beta) \Big\}\\[8pt] &\cos \alpha \sin \beta = {1 \over 2} \Big\{\sin(\alpha + \beta) - \sin (\alpha - \beta)\Big\}\\[8pt] &\cos \alpha \cos \beta = {1 \over 2} \Big\{ \cos (\alpha + \beta) + \cos (\alpha - \beta)\Big\}\\[8pt] & \sin \alpha \sin \beta = -{1 \over 2} \Big\{\cos (\alpha + \beta) - \cos(\alpha - \beta)\Big\} \end{align*}

이번 글에서는 위 공식을 모두 유도해봐요.

1. 삼각함수 곱을 합과 차로 바꾸는 곱셈 공식

1-1. 첫번째 공식

삼각함수 곱을 합으로 바꾸는 첫번째 공식을 유도해 봐요.

sin⁡(α+β)+sin⁡(α−β)=sin⁡αcos⁡β+cos⁡αsin⁡β           +sin⁡αcos⁡β−cos⁡αsin⁡β=2sin⁡αcos⁡β(1)\tag{1} \begin{align} \sin(\alpha + \beta) + \sin (\alpha - \beta) &= \sin \alpha \cos \beta + {\cancel{\cos \alpha \sin \beta}} \\ &~~~~~~~~~~~+\sin \alpha \cos \beta - {\cancel{\cos \alpha \sin \beta}}\\ &=2 \sin \alpha \cos \beta \end{align}

윗 식은 삼각함수의 합차공식을 적용한 것인데요. 만일 α\alpha와 β\beta가 동일한 값을 갖는다면 두배각공식으로 응용되는 식이에요.

(1)식을 우변에 대해 정리하면 첫번째 공식이 다음과 같이 얻어집니다.

sin⁡αcos⁡β=12{sin⁡(α+β)+sin⁡(α−β)}(2)\tag{2} \sin\alpha \cos \beta = {1 \over 2} \Big\{ \sin(\alpha + \beta) + \sin (\alpha - \beta) \Big\}

1-2. 두번째 공식

두번째 공식을 유도해 봐요.

sin⁡(α+β)−sin⁡(α−β)=sin⁡αcos⁡β+cos⁡αsin⁡β           −sin⁡αcos⁡β+cos⁡αsin⁡β=2cos⁡αsin⁡β(3)\tag{3} \begin{align} \sin(\alpha + \beta) - \sin (\alpha - \beta) &= {\cancel{\sin \alpha \cos \beta}} + {{\cos \alpha \sin \beta}} \\ &~~~~~~~~~~~-{\cancel{\sin \alpha \cos \beta}} + {{\cos \alpha \sin \beta}}\\ &=2 \cos \alpha \sin \beta \end{align}

윗 식의 우변에 대해 정리하면 두번째 공식이 다음과 같이 얻어집니다.

cos⁡αsin⁡β=12{sin⁡(α+β)−sin⁡(α−β)}(4)\tag{4} \cos\alpha \sin \beta = {1 \over 2} \Big\{ \sin(\alpha + \beta) - \sin (\alpha - \beta) \Big\}

1-3. 세번째 공식

세번째 공식을 유도해 봐요.

cos⁡(α+β)+cos⁡(α−β)=cos⁡αcos⁡β−sin⁡αsin⁡β           +cos⁡αcos⁡β+sin⁡αsin⁡β=2cos⁡αcos⁡β(5)\tag{5} \begin{align} \cos(\alpha + \beta) + \cos (\alpha - \beta) &= \cos \alpha \cos \beta - {\cancel{\sin \alpha \sin \beta}}\\ &~~~~~~~~~~~+\cos \alpha \cos \beta +{\cancel{ \sin \alpha \sin \beta}}\\ &=2 \cos \alpha \cos \beta \end{align}

윗 식의 우변에 대해 정리하면 세번째 공식이 다음과 같이 얻어집니다.

cos⁡αcos⁡β=12{cos⁡(α+β)+cos⁡(α−β)}(6)\tag{6} \cos \alpha \cos \beta = {1 \over 2} \Big\{ \cos (\alpha + \beta) + \cos (\alpha - \beta) \Big\}

1-4. 네번째 공식

네번째 공식을 유도해 봐요.

cos⁡(α+β)−cos⁡(α−β)=cos⁡αcos⁡β−sin⁡αsin⁡β           −cos⁡αcos⁡β−sin⁡αsin⁡β=−2sin⁡αsin⁡β(7)\tag{7} \begin{align} \cos(\alpha + \beta) - \cos (\alpha - \beta) &= {\cancel{\cos \alpha \cos \beta}}-\sin\alpha\sin\beta\\ &~~~~~~~~~~~-{\cancel{\cos \alpha \cos \beta}} - \sin \alpha \sin \beta\\ &=-2 \sin \alpha \sin \beta \end{align}

윗 식의 우변에 대해 정리하면 네번째 공식이 다음과 같이 얻어집니다.

sin⁡αsin⁡β=−12{cos⁡(α+β)−cos⁡(α−β)}(8)\tag{8} \sin \alpha \sin \beta = - {1 \over 2} \Big\{ \cos(\alpha + \beta) - \cos (\alpha - \beta) \Big\}

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 1 Average: 5]

Related posts.

cot(wt) 적분cot(wt) 적분 (csc(wt))^2 적분(csc(wt))^2 적분 이차방정식 풀이 벡터 화살표 그리기 | WolframAlpha 상수계수를 갖는 제차 이계 상미분 방정식 해의 모양제차 이계 상미분 방정식 : 상수 계수 함수의 그래프 그리기 | WolframAlpha 상미분방정식 풀이 | WolframAlpha Show 명령어 : Mathematica

1 thought on “삼각함수 곱을 합으로 바꾸는 공식 : 곱셈 공식”

  1. Pingback: 삼각함수의 직교성 - ilovemyage

Leave a Comment