연속 전하 분포의 에너지

BallPen · 2024-07-19T08:56:31+09:00

연속 전하 분포의 에너지 공식을 유도합니다. 연속 전하 분포의 공간을 무한대로 확대하면 면적분과 부피적분 항의 합이 얻어집니다. 이때 무한대인 곳에서의 선속은 0이므로 면적분 항은 0이 됩니다. 이를 통해 축전기에 저장된 에너지를 구할 수 있어요.

Last Updated on 2024-07-19 by BallPen

전하가 연속적으로 분포된 공간의 에너지는 얼마나 될까요?

연속 전하 분포의 에너지 공식이 어떻게 표현되는지를 이번 글에서 함께 알아봐요.

지난 글에서 전하들이 띄엄 띄엄 모여진 점전하 분포의 에너지에 대해 알아봤는데요. 그 점전하 분포들이 연속적으로 분포된 경우를 연속 전하 분포라고 해요.

결론부터 말씀드리면 무한대 크기의 공간에서 연속 전하 분포에 저장된 에너지는 다음과 같이 주어집니다.

\begin{align*} W = {{\epsilon_0}\over{2}} \int_{all~space} E^2 d \tau \end{align*}

그리고 위 공식을 축전기에 적용하면, 축전기에 저장된 에너지는 다음과 같이 표현됨을 얻을 수 있어요.

\begin{align} W = {1 \over 2} {{Q^2}\over{C}} \end{align}

그렇다면 위 공식들이 어떻게 만들어졌는지 궁금하죠? 그러면 아래의 내용을 읽어보면 도움이 될거에요.

이번 글의 목차입니다.

Contents

1. 점전하 분포의 에너지
2. 연속 전하 분포의 에너지
- 2-1. 연속 전하 분포가 포함된 무한대 공간의 에너지
- 2-2. 연속 전하 분포가 포함되지 않은 공간에서의 에너지
  - [평행판 축전기에 저장된 에너지 공식 #1]
  - [평행판 축전기에 저장된 에너지 공식 #2]
3. 연속 전하 분포의 에너지 관련 예제

이 글에서 사용된 이미지 원본은 아래에서 다운받을 수 있어요. 맥의 키노트로 작성되었습니다.

키노트 파일: continuous_charge_distribution.key

1. 점전하 분포의 에너지

전하를 하나씩 하나씩 무한대로부터 어떤 지점에 모아두었을 때 그 점전하 분포에 저장된 에너지는 다음과 같이 주어집니다. 이 에너지는 전하를 모으기 위해 이동시키는 과정에서 해준 일과 같아요.

\tag{1-1} W = {1 \over 2} \sum_{i=1}^{n} q_i V(r_i)

이때 $q_i$ 는 $i$ 번째 전하의 전하량이며, $V(r_i)$ 는 $i$ 번째 전하가 옮겨지는 위치에서 다른 전하들에 의해 만들어진 전위를 뜻합니다.

2. 연속 전하 분포의 에너지

(1-1)식의 점전하 분포의 에너지 공식을 연속 전하 분포의 에너지 공식으로 바꾸기 위해서는 시그마를 적분기호로 바꾸어 주면 됩니다.

3차원 공간의 경우를 가정하면 그 결과는 다음과 같아요.

\tag{2-1} \begin{align} W &= {1 \over 2} \int V dq\\[10pt] &={1 \over 2} \int \rho V d\tau\\[10pt] \end{align}

여기서 부피전하밀도 $\rho$ 를 도입함으로써 $dq = \rho d \tau$ 의 관계를 적용했습니다. 물론 $d \tau$ 는 미소 부피를 뜻해요.

그러면 (2-1)식에 전기장의 발산 공식인 $\nabla \cdot \vec E = {{\rho}\over{\epsilon_0}}$ 을 적용해볼께요. 그러면 $\rho = \epsilon_0 (\nabla \cdot \vec E)$ 가 되므로 다음과 같습니다.

\tag{2-2} W= {{\epsilon_0}\over{2}} \int {\color {red}(\nabla \cdot \vec E)V} d \tau

한편 벡터항등식 $\nabla \cdot (f \vec A) = {\color{red}(\nabla \cdot \vec A) f} + \vec A \cdot (\nabla f)$ 의 관계를 (2-2)식에 적용해보세요. 빨강색으로 표현된 부분이 형태가 같은 부분입니다.

\tag{2-3} \begin{align} W &= {{\epsilon_0}\over{2}} \int \Big[ \nabla \cdot(V\vec E) {\color {blue}-} \vec E \cdot {\color{blue}(\nabla V)} \Big] d\tau\\[10pt] &={{\epsilon_0}\over{2}} \int \Big[ \nabla \cdot(V\vec E) + \vec E \cdot {\color{blue}\vec E} \Big] d\tau\\[10pt] &={{\epsilon_0}\over{2}} \int \Big[ \nabla \cdot {\color{red}(V\vec E)} + E^2 \Big] d\tau\\[10pt] \end{align}

윗 식에서 전기장과 전위 사이의 관계식인 $\vec E = - \nabla V$ 를 첫번째 줄에 적용하면 두번째 줄이 됩니다.

한편 윗 식의 가장 마지막줄 빨강색 부분을 하나의 덩어리로 보면 전기장의 발산 공식인 $\int_V (\nabla \cdot \vec E )d \tau = \oint_s \vec E \cdot d \vec a$ 가 성립함을 알 수 있어요.

그 관계를 적용하면 다음과 같아질 거에요.

\tag{2-4} W = {{\epsilon_0}\over{2}} \Big(\oint_s V\vec E \cdot d \vec a + \int_V E^2 d \tau \Big)

윗 식과 같이 연속전하분포에 저장된 에너지는 두개의 항으로 구성되는데요. 첫번째 항은 면적분으로 주어지고 두번째 항은 부피적분으로 주어져요.

2-1. 연속 전하 분포가 포함된 무한대 공간의 에너지

(2-4)식의 개념을 확대하기 위해 연속전하분포가 무한대 공간의 어느 한 지점에 있다고 했을 때 그 무한대 공간 안에 저장된 에너지를 생각해봐요.

이렇게 생각하는 이유는 어느 한 지점에 연속전하분포를 만들기 위해서는 무한대에 있는 전하를 끊임없이 이동시켜야 하고, 이 과정에서 투입된 일이 연속전하분포에 저장된 에너지가 됩니다. 이를 반대로 생각하면 연속전하분포에 저장된 총 에너지를 구하기 위해서는 적분 공간을 무한대까지 확대해야 무한대로부터 전하를 이동시킬 때 투입된 일과 같아지는거에요.

그런데 공간을 무한대로 확장하면 (2-4)식의 면적적분 항은 0이 됩니다. 왜냐면 $V \vec E$ 를 하나의 어떤 벡터량으로 본다면 면적적분은 그 벡터량의 선속에 해당합니다. 마치 가우스 법칙처럼 생각해보자는 거에요.

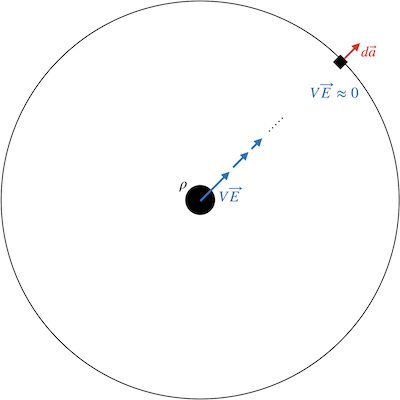
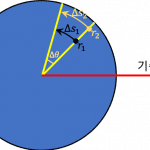
[그림 1] 연속전하분포로부터 무한대만큼 떨어진 곳의 <span class="katex-eq" data-katex-display="false">V \vec E</span>는 0으로 근사할 수 있습니다. — [그림 1] 연속전하분포로부터 무한대만큼 떨어진 곳의 $V \vec E$ 는 0으로 근사할 수 있습니다.

그런데 $r$ 이 유한한 곳에서는 전위 $V$ 와 전기장 $\vec E$ 의 곱 $V \vec E$ 는 유한한 크기를 갖는 벡터가 될거에요. 그런데 [그림 1]과 같이 $r$ 이 무한대가 되면 $V$ 는 $1 \over r$ 에 비례하고, $\vec E$ 의 크기는 $1 \over {r^2}$ 에 비례하므로 $r$ 이 커질수록 $V \vec E$ 는 점점 작아져 무한대인 곳에서는 0이 될 것을 짐작할 수 있어요.

따라서 무한대인 곳에서 [그림 1]에 나타낸 미소 구면 $d \vec a$ 를 통과하는 $V \vec E$ 의 선속은 0으로 볼 수 있고, 이를 확장해서 전체 구면의 선속을 생각하더라도 0이 되는 거에요.

반면에 (2-4)식의 부피적분은 0이 아닌데요. 이 경우에도 물론 무한대인 곳에서의 전기장의 크기 $E$ 는 0으로 볼수 있지만, [그림 1]의 부피 안에는 전기장이 0이 아니기 때문이에요.

따라서 연속 전하 분포를 포함한 무한대 공간(즉, all space)에 저장된 에너지는 다음과 같습니다.

\tag{2-5} W = {{\epsilon_0}\over{2}} \int_{all~space} E^2 d \tau

여기서 중요한 것은 공간안에 전기장 $E$ 가 존재한다면 에너지 $W$ 가 존재한다는 거에요. 그래서 “에너지는 전기장의 형태로 저장된다”라고 말합니다.

2-2. 연속 전하 분포가 포함되지 않은 공간에서의 에너지

이번에는 연속전하분포가 포함되지 않은 공간에서의 에너지를 구해 봐요. 물론 이 공간 안에 전하는 없지만 전기장이 있는 경우를 생각해 봐요.

이에 대한 대표적 예가 평행판 축전기에 저장된 에너지를 구해보는 거에요.

[평행판 축전기에 저장된 에너지 공식 #1]

아래 그림은 평행판 축전기의 모습을 나타냅니다.

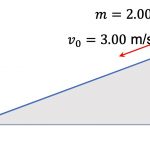
[그림 2] 평행판 축전기에 저장된 에너지는 연속전하 분포의 에너지 개념으로 구할 수 있습니다. 단 가우스 곡면 안에 연속 전하가 없는 경우에 해당하죠.

판의 면적은 $A$ 이고, 판 사이의 거리는 $d$ 에요. 그리고 판에 저장된 면전하밀도는 $\sigma$ 입니다.

그림에 표기한 파랑색 선처럼 두 판사이 공간에 저장된 에너지를 구해 볼께요. 중요한 것은 저 공간안에 연속전하가 없다는 거에요. 단지 전기장만 있을 뿐이죠.

그럼 저 위에 있는 (2-4)식을 아래에 다시 쓸게요.

\tag{2-6} W = {{\epsilon_0}\over{2}} \Big(\oint_s V\vec E \cdot d \vec a + \int_V E^2 d \tau \Big)

이때 면적분은 위에서 말씀 드렸듯이 닫혀진 면을 통과하는 $V \vec E$ 의 선속을 뜻해요. 가우스 법칙에서 말씀드렸듯이 닫혀진 가우스 면 안에 전하가 없으면 선속은 0이 됩니다.

왜냐면 들어오는 선속과 나가는 선속이 같기 때문이에요. 결국 이번에도 (2-6)식의 첫번째 항은 0이 됩니다. 그러면 남게되는 것은 이번에도 부피적분 뿐이에요.

\tag{2-7} W = {{\epsilon_0}\over{2}} \int_V E^2 d \tau

이때 평행판 면적 $A$ 에 비해 두 판사이의 거리 $d$ 가 아주 작다면 무한 평행판 사이의 전기장으로 근사할 수 있어요. 그러면 두 판사이의 전기장 크기는 ${{\sigma}\over{\epsilon_0}}$ 로 상수가 됩니다.

그러면 전기장 크기 $E$ 는 (2-7)식에서 적분기호 밖으로 나갈수 있게 되고 전체 공간 $V$ 는 판의 면적 $A$ 와 그 사이의 거리 $d$ 의 곱으로 주어집니다.

이것을 식으로 표현하면 다음과 같아요. 이때 $V$ 는 전압이 아니라 평행판 사이의 공간이 차지하는 부피를 뜻하는 것임을 주지하세요.

\tag{2-8} \begin{align} W &= {{\epsilon_0}\over{2}} \int_V E^2 d \tau \\[10pt] &={1 \over 2}\epsilon_0E^2 \int_V d \tau\\[10pt] &={1 \over 2}\epsilon_0E^2 V\\[10pt] &={1 \over 2}\epsilon_0 \Big({{\sigma}\over{\epsilon_0}} \Big)^2 (Ad) \\[10pt] &={1 \over 2} {{\sigma^2}\over{\epsilon_0}} (Ad) \\[10pt] \end{align}

또한 윗식의 세번째 줄을 이용해 축전기 사이에 저장된 단위부피당 에너지 밀도 $W \over V$ 를 정의하면 다음과 같아요.

\tag{2-9} {W \over V} = {1 \over 2} \epsilon_0 E^2

[평행판 축전기에 저장된 에너지 공식 #2]

평행판 축전기에 저장된 에너지는 (2-8)식으로 표현될 수 있잖아요. 그런데 평행판 축전기에서 중요한 변수는 축전기 공식 $Q=CV$ 와 같이 축전기에 저장된 전하량 $Q$ 와 전기용량 $C$ 잖아요.

그래서 (2-8)식의 마지막 줄을 전기용량 $C={{\epsilon_0 A}\over{d}}$ 와 면전하밀도 $\sigma={Q \over A}$ 에 대한 개념을 이용해 변형하면 다음 식이 얻어집니다.

\tag{2-10} \begin{align} W &= {1 \over 2} {{\sigma^2}\over{\epsilon_0}} (Ad) \\[10pt] &= {1 \over 2} {1 \over \epsilon_0} \Big({{Q^2}\over{A^2}}\Big) \Big(Ad \Big)\\[10pt] &={1 \over 2} \Big({{d}\over{\epsilon_0 A}} \Big) Q^2\\[10pt] &={1 \over 2} {{Q^2}\over{C}} \end{align}

3. 연속 전하 분포의 에너지 관련 예제

반지름 $R$ 인 구 껍질에 전하량 $q$ 가 균일하게 분포되어 있을 때 그 껍질에 저장된 총 에너지를 구하여라.

(풀이) 이 문제는 (2-5)식을 이용하면 풀 수 있어요.

그런데 무한대 거리에서 유한한 반지름 $R$ 을 갖는 구 껍질을 보면 하나의 점전하로 취급할 수 있으니 전기장은 점전하에 의한 전기장으로 바꿀 수 있어요.

아울러 부피적분을 위해 구면좌표계의 미소부피요소를 적용합니다.

\tag{eq-1} \begin{align} W &= {{\epsilon_0}\over{2}} \int_{all~space} E^2 d \tau \\[10pt] &={{\epsilon_0}\over{2}} \int_{all~space} \Big({{1}\over{4 \pi \epsilon_0 }}{{q}\over{r^2}}\Big)^2 r^2 dr \color{blue}\sin \theta d \theta d \phi \end{align}

이때 피적분함수가 $r$ 에만 의존하므로, 위 식에서 파랑색 부분만 먼저 적분하면 다음과 같이 $4 \pi$ 가 됩니다.

\tag{eq-2} \begin{align} \int_{all~space} \sin \theta d \theta d \phi &= \int_{0}^{2 \pi} \int_{0}^{\pi} \sin \theta d \theta d \phi\\[10pt] &=\int_{0}^{2 \pi} \Big[ -\cos \theta \Big]_{0}^{\pi} d \phi\\[10pt] &=2\int_{0}^{2 \pi} d \phi\\[10pt] &=2 \Big[ \phi\Big]_0^{2\pi}\\[10pt] &=4 \pi \end{align}

그러면 (eq-2)식을 (eq-1)식에 대입하여 정리하면 다음과 같아요.

\tag{eq-3} \begin{align} W &= {{4 \pi \epsilon_0 q^2}\over{2 (4 \pi \epsilon_0)^2}} \int_R^\infty \Big({1 \over{r^2}} \Big)^2 r^2 dr \\[10pt] &={{q^2}\over{8 \pi \epsilon_0}} \Big[-{1 \over r} \Big]_R^{\infty}\\[10pt] &={1 \over{8 \pi \epsilon_0}} {{q^2}\over{R}} \end{align}

이때 적분 구간은 구 껍질의 반지름 $R$ 부터 무한대까지 임을 주지하시기 바랍니다.

흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.

[Total: 1 Average: 5]