전기장의 회전(Curl of Electric Field)

Last Updated on 2024-04-28 by BallPen

점전하가 만드는 전기장의 회전과 물리적 의미를 알아 봐요.

전기장의 회전(curl)과 그 물리적 의미를 알아보겠습니다.

점전하가 만드는 전기장에 대한 스토크스의 정리(Stokes’ theorem)는 다음 식과 같이 0이 됩니다.

\tag{D1}
\oint_c \vec E \cdot d \vec l = \int_s ({\color{red}\nabla \times \vec E}) \cdot d \vec a = 0

이때 윗식에서 빨강색으로 표기한 \nabla \times \vec E 를 전기장의 회전이라고 하는데요. 그것만을 따로 쓰면 다음식이 성립해요.

\tag{D2}
\nabla \times \vec E =0,~~~~~\vec E = - \nabla V

그렇다면 과연 (D2)식은 어떻게 유도된 걸까요? 함께 알아봐요.

아래는 이번 글의 목차입니다.

1. 점전하에 의한 전기장 복습

점전하의 전하량을 +q라 할 때 그 점전하에 의한 전기장은 다음 식과 같이 주어집니다.

\tag{1-1}
\vec E(\vec r) = {1 \over{4 \pi \epsilon_0}} {{q}\over{r^2}} \hat r

그리고 위 (1-1)식의 벡터장을 매쓰매티카로 그리면 아래 [그림 1]과 같아요.

전하로부터 멀리 떨어질수록, 즉 r이 클수록 전기장 화살표의 길이가 짧아지므로 전기장의 크기가 급격히 작아짐을 알 수 있어요.

또한 단위벡터가 지름방향 \hat r로 되어 있으므로 전기장의 방향은 중심으로부터 나가는 방향을 향합니다.

2. 전기장의 회전

이제부터 본격적으로 전기장의 회전에 대해 시작할건데요. 이를 위해 우선 전기장에 대한 선적분을 해봐요.

이걸 왜 하냐면, 스토크스 정리를 적용하려고 하기 때문이에요. 나중에 알겠지만 전기장에 대한 선적분의 결과를 통해 전기장의 회전이 어떻게 주어지는지를 알게 됩니다.

2-1. 전기장의 선적분

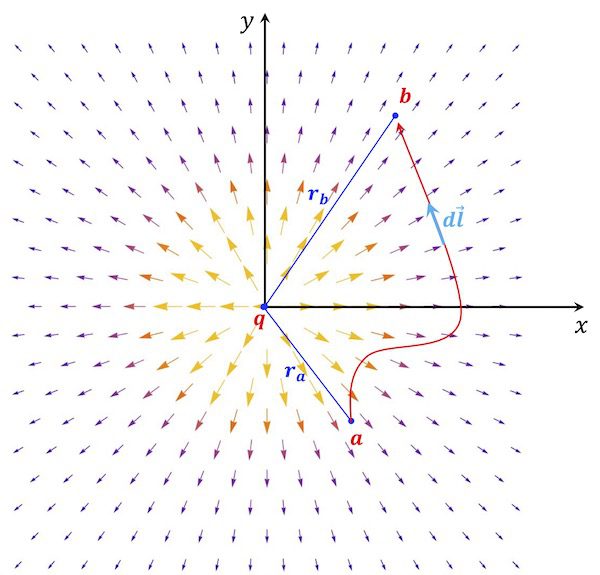
아래 [그림 2]는 점전하에 의한 전기장을 화살표로 그린 거에요. 그리고 전하가 있는 중심으로부터 r_a만큼 떨어진 a점에서 r_b만큼 떨어진 b점까지 선적분 해봐요.

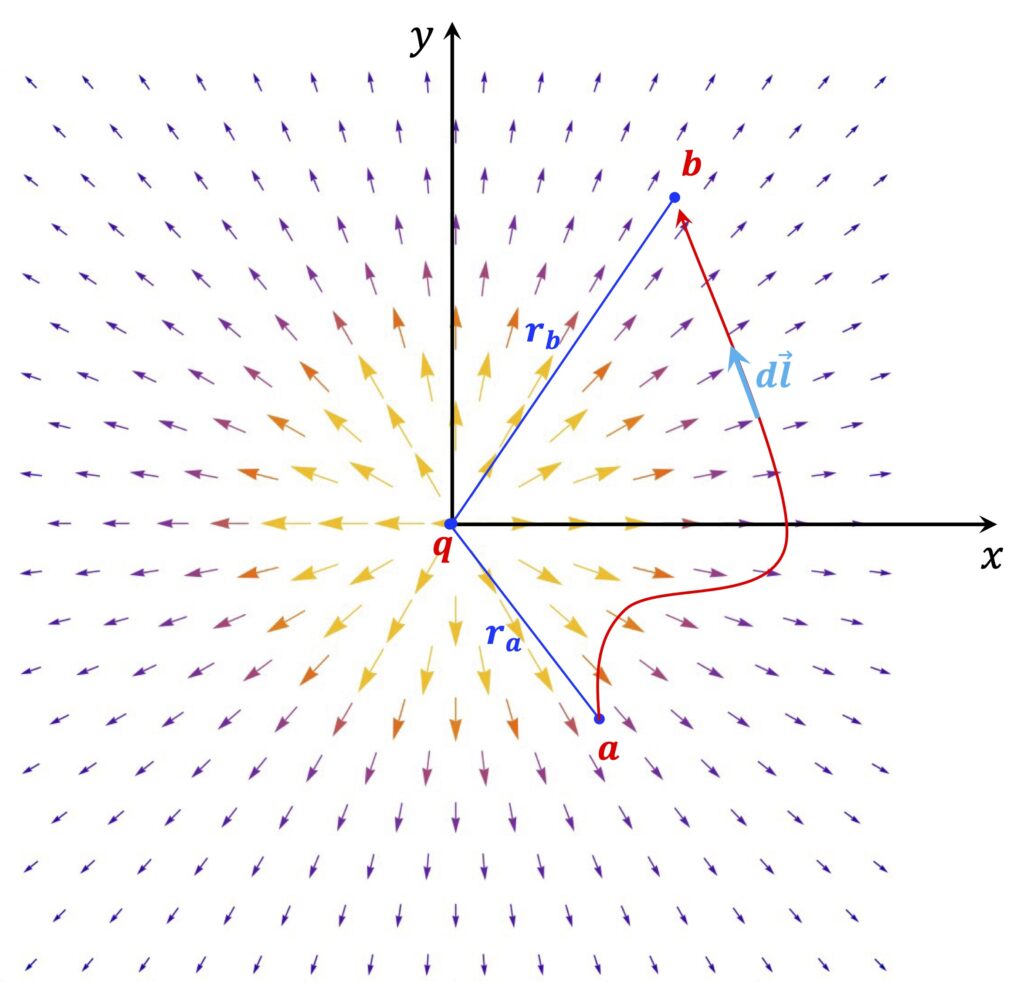
이를 식으로 쓰고 전개하면 아래 (2-1)식과 같아요.

이때 빨강색으로 표기한 부분은 구면좌표계의 미소길이입니다. 그리고 단위벡터끼리의 스칼라 곱을 하면 평행한 성분은 1이 되고 수직한 성분은 0이되므로 세번째 줄이 성립됩니다.

\tag{2-1}
\begin{align}
\int_a^b \vec E \cdot d \vec l &= {q \over {4 \pi \epsilon_0}} \int_{r_a} ^ {r_b} {1 \over {r^2}} d \hat r \cdot d \vec l \\[10pt]
&={q \over {4 \pi \epsilon_0}} \int_{r_a} ^ {r_b} {1 \over {r^2}} d \hat r \cdot \color{red}(dr\hat r + rd\theta \hat \theta + r\sin \theta d\phi \hat \phi)\\[10pt]
&={q \over {4 \pi \epsilon_0}} \int_{r_a} ^ {r_b} {1 \over {r^2}} d r\\[10pt]
&={q \over {4 \pi \epsilon_0}} \Big[ -{1 \over r} \Big]_{r_a}^{r_b}\\[10pt]
&={q \over {4 \pi \epsilon_0}}\Big({1 \over r_a} - {1 \over r_b} \Big)
\end{align}

그 결과 전기장의 선적분은 경로에 무관하고 양 끝점 r_a와 r_b값에만 의존하는 것을 알 수 있어요.

이게 무슨 말이냐면 위 (2-1)식의 가장 마지막 줄에서 {{q}\over{4 \pi \epsilon_0}}는 모두 이미 알고 있는 상수에요. 그러므로 전기장의 선적분은 r_a와 r_b만 알면 계산할 수 있고 그 사이의 경로가 어떻든 상관없다는 뜻이에요.

그럼 양 끝점에만 의존하는 (2-1)식의 가장 마지막 줄을 기호 V로 치환하여 간단하게 정리해봐요.

\tag{2-2}
\begin{align}
\int_{a}^{b} \vec E \cdot d \vec l &= {q \over {4 \pi \epsilon_0}}{1 \over r_a} - {q \over {4 \pi \epsilon_0}}{1 \over r_b}\\[10pt]
&=V(a) - V(b)
\end{align}

그리고 V(a)를 a점에서의 전위(또는 전압, Voltage), V_b를 b점에서의 전위라고 부릅니다.

결국 [그림 2]와 같이 a점에서 b점까지 선적분한 결과는 (2-2)식과 같이 a점에서의 전위와 b점에서의 전위의 변화량 -\Delta V와 같습니다.

여기서 전위의 변화량에 음의 부호를 붙인 이유는 변화량은 나중값에서 처음값을 빼야 하는데 (2-2)식에서는 처음값에서 나중값이 빠지기 때문이에요

2-2. 전위

(2-2)식처럼 전기장을 선적분하면 전위의 변화량을 구할 수 있다는 것을 알게 되었어요. 그렇다면 전위의 변화량이 아닌 한 지점에서의 절대적인 전위 값을 구하는 식은 어떻게 정의할 수 있을까요?

이를 위해서는 전압이 0이 되는 지점을 정하고 그 점을 기준으로 임의 점에서의 전위를 구하는 방식으로 접근합니다.

일단 (2-2)식의 양변에 마이너스 부호를 붙이면 아래의 (2-3)식이 성립할거에요. 여기서 마이너스 부호를 붙이는 이유는 전위의 나중값에서 처음값을 빼는 형태로 식을 바꾸고 싶은 것 뿐입니다.

그리고 하나만 더 생각해서 a점을 출발해서 전위가 0인 o점을 거쳐 b로 갔다고 생각해봐요. 어차피 양 끝점에만 의존하고 경로에 무관하니 이렇게 설정해도 전혀 문제가 없어요.

\tag{2-3}
\begin{align}
- \int_a^b \vec E \cdot d \vec l &= - \Big(\int_a^o \vec E \cdot d \vec l + \int_o^b \vec E \cdot d \vec l \Big)\\[10pt]
 &=- \int_o^b \vec E \cdot d \vec l - \Big(-\int_o^a \vec E \cdot d \vec l \Big)\\[10pt]
&=V(b) - {\cancel {V(o)}} - (V(a) - \cancel {V(o)})\\[10pt]
&=V(b) - V(a)
\end{align}

결국 윗 식에서 - \int_o^b \vec E \cdot d \vec l 가 b점에서의 전위 V(b)인 것처럼 임의점에서의 전위는 다음과 같이 정의됩니다.

\tag{2-4}
V(r) = - \int _o ^ {r} \vec E \cdot d \vec l

이때 전위가 0이 되는 o점을 reference point라고 부릅니다. 보통은 점전하로부터 무한대만큼 떨어진 지점을 reference point로 간주하고 V(o)=0으로 정합니다.

2-3. 전기장의 회전

그렇다면 만일 a점에서 출발하여 임의의 경로를 거친 후 다시 제자리인 a점으로 돌아온다면 전기장의 선적분은 어떻게 될까요?

즉 한 지점에서 출발하여 다시 그 지점으로 돌아온 것이므로 닫힌 경로가 되겠죠. 이를 식으로 표현하며 다음과 같을 거에요.

\tag{2-5}
\begin{align}
-\oint_c \vec E \cdot d \vec l = V(a) - V(a) = 0
\end{align}

위 식에서 적분기호 아래에 있는 c는 닫힌 경로임을 뜻해요. 그 결과 닫힌 경로에 대한 전기장의 선적분은 처음과 나중의 전위가 같으므로 0이 됩니다.

그럼 이제 (2-5)식의 관계를 스토크스 정리에 대입해서 정리해볼께요.

\tag{2-6}
-\oint_c \vec E \cdot d \vec l = 0 = -\int_s ({\color{red}\nabla \times \vec E}) \cdot d \vec a

결국 위 식이 성립하기 위해서는 \nabla \times \vec E에 대한 면적적분도 0이 되어야 합니다. 이때 기호 s는 닫힌 경로 c가 만든 그 안쪽의 면적을 뜻해요.

면적적분이 0이 되기 위해서는 빨강색으로 표시한 \nabla \times \vec E, 즉 전기장의 회전이 0이 되어야만 합니다. 다음 식이 성립한다는 것이죠.

\tag{2-7}
\nabla \times \vec E = 0

또한 스칼라함수에 대한 기울기의 회전은 항상 0이잖아요. 그래서 다음 식도 성립합니다.

\tag{2-8}
\vec E = - \nabla V

여기서 음의 부호는 전기장의 방향이 전위가 감소하는 쪽을 향함을 뜻해요.

그런데 (2-8)식에서 갑자기 전위 V가 나와 당황스러울텐데요. (2-8)식을 (2-4)식에 대입해서 정리하면 아래 (2-9)식처럼 실제로 전위가 나오는 것을 알 수 있어요.

\tag{2-9}
\begin{align}
V(r) &= - \int _o ^ {r} \vec E \cdot d \vec l\\[10pt]
&=-\int_o^{r} -\nabla V \cdot d \vec l\\[10pt]
&= \int_o^{r} \Big( {{\partial V}\over{\partial r}}\hat r \Big) \cdot (dr \hat r)\\[10pt]
&=\int_o^{r} {{\partial V}\over{\partial r}} dr\\[10pt]
&=\int_o^{r} dV\\[10pt]
&=V(r) - V(o)\\[10pt]
&=V(r)
\end{align}

여기서 V(o)=0인데요. 그 이유는 전위가 0인 reference point 이기 때문이네요. 양변이 같으므로 결국 (2-8)식이 성립한다는 것을 뜻해요.

3. 전기장의 회전 의미

(2-7)식처럼 전기장의 회전, 즉 \nabla \times \vec E =0이라는 의미는 전기장이 벡터 보존장임을 뜻합니다.

또한 벡터 보존장은 어떤 스칼라함수의 기울기가 되어야 하는데요. 그 관계가 (2-8)식이 되겠습니다.

아울러 보존장의 선적분은 경로에 의존하지 않고 시작과 끝점에 의해 결정되는 특징을 갖습니다.

Related posts.

자동차 사양서 – 토크, 등급, CO2, 정부 공인 표준 연비 등의 제원 설명 자동차 배기량(displacement)의 정의와 어떻게 계산하는지를 알아볼까요? 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 인공지능 기술 분야. 중소기업은 머신러닝 중심, 그럼 대기업은? 밀도 정의와 활용 사례 단위 표기 오류가 있는 도쿄 올림픽 중계방송이 불편한 이유 등가소음도 계산 방법 알려 드립니다. 음압레벨도 함께 공부해요. 선풍기 살 때 풍량 효율 큰 것 고르면 되는 거에요?