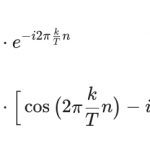이항정리 – 이항식의 거듭제곱에 대한 근사

Last Updated on 2024-01-06 by BallPen

이항식의 거듭제곱을 다항식으로 근사하는 이항정리를 알아보겠습니다.

이항정리 근사로 이항식의 거듭제곱을 아주 간결한 다항식으로 표현할 수 있어요.

과연 이항정리란 무엇이고 이를 적용하기 위한 조건은 무엇인지 알아보겠습니다.

아래는 이번 글의 목차입니다.

1. 이항정리

1-1. 이항정리 공식

이항정리란 이항식의 거듭제곱을 다항식으로 표현하는 방법을 말하는데요. 여기서 이항식이란 두개의 항으로 주어진 식을 말합니다.

근사식을 만들기 위해 많이 사용되는 이항정리 공식은 아래 (1)식과 같습니다. 이 식이 유도되는 과정은 하단에 별도로 정리하도록 하겠습니다.

\tag{1}
\begin{align}
(1+x)^n = 1+ nx + {{n(n-1)}\over{2 !}}x^2 + {{n(n-1)(n-2)}\over{3!}}x^3 + \cdots
\end{align}

(1)식의 좌변은 1과 x로 구성된 이항식이고, 이 이항식이 n제곱으로 주어져 있습니다. 이러한 형태의 식을 이항식의 거듭제곱이라 부릅니다.

이항식의 거듭제곱은 (1)식의 우변과 같이 다항식의 형태로 표기될 수 있어요. 다항식으로 표현하면 복잡한 수식을 간단하게 근사할 수 있을 뿐만 아니라 미분이나 적분을 쉽게 할 수 있습니다.

한편 (1)식의 우변에서 ! 표시를 볼 수 있어요. 이것은 팩토리얼(factorial)이라고 부르는 표기입니다.

예를 들어 n!은 n\times(n-1)\times(n-2)\times\cdots\times2\times1로 계산됩니다. 0!부터 5!에 대한 계산 예는 아래와 같습니다.

\tag{2}
\begin{align}
0! &= 1\\
1! &= 1\\
2! &= 2 \times 1 =2\\
3! &= 3 \times 2 \times 1 = 6\\
4! &= 4 \times 3 \times 2 \times1 = 24 \\
5! &= 5 \times 4 \times 3 \times 2 \times 1 = 120
\end{align}

그런데 (2)식의 가장 첫줄을 보면 0! 이 1이에요. 1!이 1이 되는 것은 이해하기 쉬운데 0!이 1인 것은 직관적으로 이해하기 어려운데요. 이를 알아보기 위해 우선 아래의 (3)식이 성립하는지를 보세요..

\tag{3}
\begin{align}
n! &= n \times(n-1)\times(n-2)\times\cdots\times3\times2\times1\\
&=n \times(n-1)!
\end{align}

분명히 성립합니다. 그렇다면 이 (3)식의 두번째 줄에 n 대신 1을 대입하면 아래와 같습니다.

\tag{4}
\begin{align}
1! &= 1 \times(1-1)!\\
&=1 \times 0 !\\
&=1
\end{align}

(4)식에서 보시는 바와 같이 1!=1이 성립하기 위해서는 0!=1이 성립해야 합니다.

1-2. 이항식 거듭제곱의 근사

이제부터 이항정리를 이용한 이항식 거듭제곱의 근사 방법과 사례를 알아보겠습니다. 저 위에 있는 (1)식이 너무 멀어 아래에 (5)식으로 다시쓰겠습니다.

\tag{5}
\begin{align}
(1+x)^n = 1+ nx + {{n(n-1)}\over{2 !}}x^2 + {{n(n-1)(n-2)}\over{3!}}x^3 + \cdots
\end{align}

아래에 주어진 이항식(1+0.005)의 8제곱을 계산기로 계산하면 1.040707044가 나옵니다.

\tag{6}
(1+0.005)^8 = 1.040707044

(5)식의 이항정리가 성립한다면 (5)식의 우변도 1.040707044가 나와야 할텐데요. x=0.005, ~n=8로 설정하고 우변의 항을 하나씩 늘려가면서 그 값을 계산해 보겠습니다.

\tag{7}
\begin{align}
1 &= 1\\
1 + nx =1+(8)(0.005)&=1.04\\
1.04 + {{n(n-1)}\over{2!}}x^2 = 1.04+{{8\times7}\over{2\times1}}(0.005)^2 &= 1.0407\\
1.0407 + {{n(n-1)(n-2)}\over{3!}}x^3 =1.0407 + {{8\times7\times6}\over{3\times2\times1}}(0.005)^3 &=1.040707
\end{align}

위 식에서 첫번째 줄은 다항식의 첫번째 항, 두번째 줄은 다항식의 두번째 항까지, 세번째 줄은 다항식의 세번째 항까지, 네번째 줄은 다항식의 네번째 항까지의 계산 결과입니다.

다항식의 항을 하나씩 늘려가면서 값을 적용해 나가면 참값에 점점 수렴하는 것을 알 수 있습니다. 이 원리를 적용한 것이 바로 이항정리 근사입니다.

보통은 이항정리 근사를 함에 있어 두번째 항까지 근사를 하는 경우가 많습니다. 물론 항의 갯수를 늘릴 수록 참값과 가까워집니다만 항이 추가되기 때문에 다시 식이 복잡해져 근사의 장점이 줄어듭니다.

그래서 이항정리 근사는 보통 아래와 같이 표현합니다.

\tag{8}
(1+x)^n \approx 1+nx

여기서 주의해야 할 것은 x의 절대값이 1보다 작은 경우에 이항정리 근사가 성립합니다. x의 절대값이 1보다 큰 경우에는 수렴하지 못하고 발산합니다.

예를 들어 x가 1보다 큰 (1+5)^8을 계산기로 계산하면 1 679 616이 나옵니다. x=5, ~n=8로 설정하고 다항식에 적용해 보겠습니다.

\tag{9}
\begin{align}
1 &= 1\\
1 + nx =1+(8)(5)&=41\\
41 + {{n(n-1)}\over{2!}}x^2 = 41+{{8\times7}\over{2\times1}}(5)^2 &= 741\\
741 + {{n(n-1)(n-2)}\over{3!}}x^3 =741 + {{8\times7\times6}\over{3\times2\times1}}(5)^3 &=7741
\end{align}

보는 바와 같이 다항식의 항의 갯수를 하나씩 늘려가더라도 참값으로 수렴하지 못하고 발산해가는 것을 알 수 있습니다.

2. 이항정리 근사 활용 사례

이항정리 근사가 적용되는 사례를 들어 보겠습니다.

예를 들어 다음의 식이 있습니다. 여기서 R_M은 화성의 반지름이고, h는 화성의 표면으로부터의 어떤 높이라고 가정하겠습니다. 그러므로 R_M은 h보다 무척 큽니다.

\tag{10}
\begin{align}
{{{R_M}^3}\over{(R_M + h)^3}}
\end{align}

이 복잡한 식을 더 간결한 형태로 근사하고 싶습니다. 어떻게 하면 될까요? 일단 아래와 같이 조금만 변형해 보겠습니다.

\tag{11}
\begin{align}
{{{R_M}^3}\over{(R_M + h)^3}} &= {{{R_M}^3}\over{{R_M}^3(1+{{h}\over{R_M}})^3}}\\
&={{1}\over{(1+{{h}\over{R_M}})^3}}\\
&=\Big(1+{{h}\over{R_M}}\Big)^{-3}
\end{align}

그리고 (11)식의 가장 마지막 식에서 괄호안에 있는 h \diagup {R_M}은 분명하게 1보다 작다는 것을 알 수 있습니다. 그러면 (8)식의 이항정리 근사를 적용해봐요.

\tag{12}
\begin{align}
{{{R_M}^3}\over{(R_M + h)^3}} &= \Big(1+{{h}\over{R_M}}\Big)^{-3}\\
& \approx 1+(-3){{h}\over{R_M}}\\
& \approx1-3 \Big({{h}\over{R_M}}\Big)
\end{align}

(12)식의 좌변과 (12)식 마지막 줄의 이항정리 근사식이 거의 비슷한지를 알아보기 위해 적당한 값을 대입해보겠습니다. 화성의 반지름 R_M = 3400~\mathrm{km}, 지표면 근처의 높이 h=1.0~\mathrm{km}로 대입하겠습니다.

계산 결과 좌변은 0.999 118 165, 우변은 0.999 117 647이 나와 거의 유사함을 알 수 있습니다. 또한 (12)식 좌변보다 이항정리가 적용된 우변의 마지막 줄이 훨씬 간결함을 알 수 있습니다.

이항정리 근사는 중력 위치에너지를 mgh로 근사하는 과정 등에서도 널리 사용됩니다.

3. 이항정리 공식 유도

지금부터는 (1)식과 (5)식의 이항정리 공식인 이항급수가 어떻게 나오게 되었는지를 설명드립니다.

이항식의 거듭제곱에 대한 몇가지 전개식이 아래에 있습니다.

\tag{13}
\begin{align}
(x+y)^0 &= 1\\
(x+y)^1 &= x+y\\
(x+y)^2 &= x^2 + 2xy + y^2 \\
(x+y)^3 &= x^3 + 3x^2 y + 3 xy^3 + y^3\\
(x+y)^4 &=x^4 + 4x^3 y + 6 x^2 y^2 + 4xy^3 + y^4
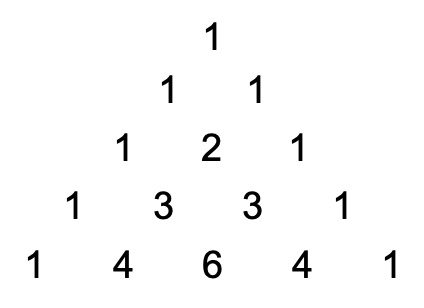
\end{align}

이때 우변 각 항의 계수를 아래 [그림 1]처럼 삼각형 모습으로 배치할 수 있는데요. 이 삼각형을 파스칼의 삼각형(Pascal’s triangle)이라고 부릅니다.

이 파스칼의 삼각형이 특이한 것은 삼각형을 구성하는 각 원소는 바로 위 두 숫자의 합으로 나타난다는 것입니다. 참 재미있죠.

예를 들어 마지막 줄 중앙에 있는 원소 6은 바로 위에 있는 숫자 3과 3의 합으로 주어진다는 이야기에요.

이러한 관계를 반영하여 (13)식의 전개식을 일반식으로 표현하면 아래와 같습니다.

\tag{14}
\begin{align}
(x+y)^n &= \sum_{k=0}^{n}{n \choose k}x^{n-k}y^{k}\\
&={n \choose0}x^n y^0 + {n \choose1}x^{n-1} y^1 + {n \choose2}x^{n-2} y^2+\cdots
\end{align}

여기서

\tag{15}
{n \choose k} =  _n C _k ={{n!}\over{k!(n-k)!}}

로 주어지는 조합(Combination)입니다. 조합이란 n개의 서로 다른 물건에서 k개를 순서와 무관하게 선택하는 경우의 수를 말합니다.

그런데 이항식의 거듭제곱이 (1+x)^n의 형태로 주어진다면 (14)식을 그대로 적용하여 아래와 같이 표현할 수 있습니다.

\tag{16}
\begin{align}
(1+x)^n &= \sum_{k=0}^{n}{n \choose k}1^{n-k} x^{k}\\
&={n \choose0}1^n x^0 + {n \choose1}1^{n-1} x^1 + {n \choose2}1^{n-2} x^2+{n \choose3}1^{n-3} x^3+\cdots\\
&={n \choose0} + {n \choose1}x^1 + {n \choose2}x^2+{n \choose3}x^3+\cdots\\
\end{align}

한편 (16)식에 주어진 이항 급수의 계수를 (15)식을 이용해 세번째 항까지 구해보면 아래와 같습니다.

\tag{17}
\begin{align}
{n \choose 0} &= {{n!}\over{0!(n-0)!}}  = 1\\
{n \choose 1} &= {{n!}\over{1!(n-1)!}} =  {{n(n-1)!}\over{1!(n-1)!}} = n\\
{n \choose 2} &= {{n!}\over{2!(n-2)!}} =  {{n(n-1)(n-2)!}\over{2!(n-2)!}} = {{n(n-1)}\over{2!}}\\
\end{align}

(17)식에서 구한 계수를 (16)식에 대입하면 최종적으로 아래의 이항정리 공식이 얻어집니다.

\tag{18}
\begin{align}
(1+x)^n = 1+ nx + {{n(n-1)}\over{2 !}}x^2 + {{n(n-1)(n-2)}\over{3!}}x^3 + \cdots
\end{align}

Related posts.

2015-2019년 대한민국 인구 추이. 50% 인구가 수도권에 살고 있는 신기한 나라 가구 소득. 여자 가구주는 연간 2,112만원, 그럼 남자는? 문화 예술 관람. 우리 영화보는거 말고 다른 거 뭐 할까요? 외국인 입국자 수와 방문 목적에 코로나19가 미친 영향 테일러 급수 증명과 활용 사례 이산 푸리에 변환 예제 사인 제곱 함수의 평균값 코사인 법칙(law of cosines)