Last Updated on 2024-12-22 by BallPen
변수분리법으로 직각좌표계에서의 라플라스 방정식을 풀어봐요.
직각좌표계에서의 라플라스방정식 공식은 다음과 같습니다.
∇ 2 V = ∂ 2 V ∂ x 2 + ∂ 2 V ∂ y 2 + ∂ 2 V ∂ z 2 = 0 \begin{align*}
\nabla ^2 V = {{\partial^2 V}\over{\partial x^2}} + {{\partial^2 V}\over{\partial y^2}} + {{\partial^2 V}\over{\partial z^2}} = 0
\end{align*} ∇ 2 V = ∂ x 2 ∂ 2 V + ∂ y 2 ∂ 2 V + ∂ z 2 ∂ 2 V = 0 이때 위 식을 만족하는 V ( x , y , z ) V(x,y,z) V ( x , y , z )
아래는 이번 글의 목차입니다.
1. 직각좌표계에서의 라플라스방정식 아래 (1-1)식에 주어진 3차원 라플라스방정식 의 해 V ( x , y , z ) V(x,y,z) V ( x , y , z ) V ( x , y , z ) V(x,y,z) V ( x , y , z )
∇ 2 V = ∂ 2 V ∂ x 2 + ∂ 2 V ∂ y 2 + ∂ 2 V ∂ z 2 = 0 (1-1) \tag{1-1}
\begin{align}
\nabla ^2 V = {{\partial^2 V}\over{\partial x^2}} + {{\partial^2 V}\over{\partial y^2}} + {{\partial^2 V}\over{\partial z^2}} = 0
\end{align} ∇ 2 V = ∂ x 2 ∂ 2 V + ∂ y 2 ∂ 2 V + ∂ z 2 ∂ 2 V = 0 ( 1-1 ) 만일 1차원 라플라스 방정식이라면 양변으로 변수를 분리 해 쉽게 해를 구할 수 있는데요. 3차원 2계 편미분 방정식으로 주어지는 라플라스 방정식은 그렇게 간단히 해를 구할 수 없어요.
그렇다고 푸는 방법이 완전히 없는 것은 아니에요. 아래에 설명드릴 변수분리법을 이용하면 해를 구할 수 있습니다. 이에 대해 구체적으로 알아봐요.
1-1. 변수분리법 가정부터 시작합니다. (1-1)식 라플라스방정식의 해 V ( x , y , z ) V(x,y,z) V ( x , y , z )
V ( x , y , z ) = X ( x ) Y ( y ) Z ( z ) (1-2) \tag{1-2}
\begin{align}
V(x,y,z) = X(x)Y(y)Z(z)
\end{align} V ( x , y , z ) = X ( x ) Y ( y ) Z ( z ) ( 1-2 ) 즉, 전압 V V V
∇ V = ∂ V ∂ x + ∂ V ∂ y + ∂ V ∂ x = Y Z d X d x + X Z d Y d y + X Y d Z d z (1-3) \tag{1-3}
\begin{align}
\nabla V &= {{\partial V}\over{\partial x}} + {{\partial V}\over{\partial y}}+ {{\partial V}\over{\partial x}}\\[10pt]
&=YZ {{dX}\over{dx}} + XZ{{dY}\over{dy}} + XY{{dZ}\over{dz}}
\end{align} ∇ V = ∂ x ∂ V + ∂ y ∂ V + ∂ x ∂ V = Y Z d x d X + XZ d y d Y + X Y d z d Z ( 1-3 ) ∇ 2 V = ∂ 2 V ∂ x 2 + ∂ 2 V ∂ x 2 + ∂ 2 V ∂ x 2 = Y Z d 2 X d x 2 + X Z d 2 Y d y 2 + Y Z d 2 Z d z 2 = 0 (1-4) \tag{1-4}
\begin{align}
\nabla^2 V &= {{\partial^2 V}\over{\partial x^2}} + {{\partial^2 V}\over{\partial x^2}} + {{\partial^2 V}\over{\partial x^2}}\\[10pt]
&=YZ{{d^2 X}\over{dx^2}} + XZ{{d^2 Y}\over{dy^2}} + YZ{{d^2 Z}\over{dz^2}} = 0 \\[10pt]
\end{align} ∇ 2 V = ∂ x 2 ∂ 2 V + ∂ x 2 ∂ 2 V + ∂ x 2 ∂ 2 V = Y Z d x 2 d 2 X + XZ d y 2 d 2 Y + Y Z d z 2 d 2 Z = 0 ( 1-4 ) 이번에는 (1-4)식의 두번째 줄 양변을 X Y Z XYZ X Y Z
1 X d 2 X d x 2 + 1 Y d 2 Y d y 2 + 1 Z d 2 Z d z 2 = 0 (1-5) \tag{1-5}
\begin{align}
{1 \over X} {{d^2 X}\over{dx^2}} + {1 \over Y} {{d^2 Y}\over{dy^2}} + {1 \over Z}{{d^2 Z}\over{dz^2}} = 0
\end{align} X 1 d x 2 d 2 X + Y 1 d y 2 d 2 Y + Z 1 d z 2 d 2 Z = 0 ( 1-5 ) 이때 위 (1-5)식의 좌변에 있는 세 항의 합이 0이어야 우변과 같아지죠. 그래서 좌변 첫째 항을 A A A B B B − ( A + B ) -(A+B) − ( A + B )
이렇게 치환하면 아래 식이 되어 (1-5)식의 우변처럼 0이 되는 것을 알 수 있어요. 즉 이렇게 치환해도 상관없다는 뜻이에요.
A + B − ( A + B ) = 0 (1-6) \tag{1-6}
A+B - (A+B) = 0 A + B − ( A + B ) = 0 ( 1-6 ) 최종적으로 (1-5)식과 치환된 (1-6)식을 비교해서 정리하면 다음의 이계 상미분 방정식 3개가 만들어집니다.
d 2 X d x 2 − A X = 0 d 2 Y d y 2 − B Y = 0 d 2 Z d z 2 + ( A + B ) Z = 0 (1-7) \tag{1-7}
\begin{align}
&{{d^2 X}\over{dx^2}} - AX = 0 \\[10pt]
&{{d^2 Y}\over{dy^2}} - BY =0\\[10pt]
&{{d^2Z}\over{dz^2}} + (A+B) Z =0
\end{align} d x 2 d 2 X − A X = 0 d y 2 d 2 Y − B Y = 0 d z 2 d 2 Z + ( A + B ) Z = 0 ( 1-7 ) 이제 이 미분방정식들을 만족하는 해를 구한 후 그 해에 경계조건을 적용하면 X ( x ) , Y ( y ) , Z ( z ) X(x), ~Y(y), ~Z(z) X ( x ) , Y ( y ) , Z ( z )
예제를 하나 풀어 봐요.
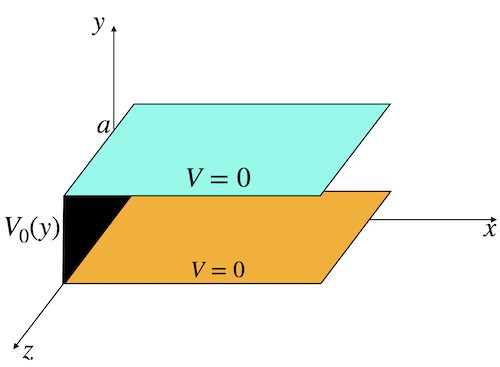
2. 예제 아래 그림과 같이 무한한 크기를 갖는 금속판 두개가 있다. 아래쪽에 있는 금속판은 ( x , z ) (x,z) ( x , z ) y = a y=a y = a V 0 ( y ) V_0 (y) V 0 ( y )
( i ) y = 0 에서 V = 0 ( i i ) y = a 에서 V = 0 ( i i i ) x = 0 에서 V = V 0 ( y ) ( i v ) x = ∞ 에서 V → 0 \begin{align*}
&({\rm i}) ~ y=0에서 ~~V=0\\
&({\rm ii}) ~ y=a에서~~ V=0\\
&({\rm iii})~x=0에서~~V=V_0 (y)\\
&({\rm{iv}})~x= \infty에서~~V \rightarrow 0
\end{align*} ( i ) y = 0 에서 V = 0 ( ii ) y = a 에서 V = 0 ( iii ) x = 0 에서 V = V 0 ( y ) ( iv ) x = ∞ 에서 V → 0
[그림 1] 직각좌표계에서의 라플라스방정식 예제. 접지된 두 평행판 사이의 전위 분포를 구하는 문제입니다.
2-1. 라플라스방정식 이 문제에서 두 판사이의 공간에는 전하밀도가 없으므로 다음의 라플라스 방정식을 만족해야 해요.
∇ 2 V = 0 (2-1) \tag{2-1}
\nabla^2 V =0 ∇ 2 V = 0 ( 2-1 ) 그럼 이제부터 (2-1)식의 해 V V V z z z x x x y y y V ( x , y ) V(x,y) V ( x , y )
그러면 (2-1)식은 아래와 같이 3차원이 아닌 2차원 직각좌표계에서의 라플라스방정식 문제에 해당합니다.
∂ 2 V ∂ x 2 + ∂ 2 V ∂ y 2 = 0 (2-2) \tag{2-2}
{{\partial^2 V}\over{\partial x^2}} + {{\partial^2 V}\over{\partial y^2}} =0 ∂ x 2 ∂ 2 V + ∂ y 2 ∂ 2 V = 0 ( 2-2 ) 2-2. 라플라스방정식의 일반해 그럼 이제부터 (2-2)식 라플라스방정식의 해를 구해 봐요. 이를 위해 앞서 설명드렸던 변수분리법을 적용합니다. (2-2)식의 해도 다음 조건을 만족한다고 가정해봐요.
V ( x , y ) = X ( x ) Y ( y ) (2-3) \tag{2-3}
V(x,y) = X(x)Y(y) V ( x , y ) = X ( x ) Y ( y ) ( 2-3 ) 그리고 (2-3)식을 (2-2)식에 대입한 후 양변을 X Y XY X Y
1 X d 2 X d x 2 + 1 Y d 2 Y d y 2 = 0 (2-4) \tag{2-4}
\begin{align}
{1 \over X} {{d^2 X}\over{dx^2}} + {1 \over Y} {{d^2 Y}\over{dy^2}} = 0
\end{align} X 1 d x 2 d 2 X + Y 1 d y 2 d 2 Y = 0 ( 2-4 ) 그런데 위 식의 관계가 성립되기 위해서는 좌변의 첫째와 둘째 항의 크기가 서로 같고 부호가 반대가 되어야 하잖아요. 그래서 임의로 첫번째 항을 k 2 k^2 k 2 − k 2 -k^2 − k 2
그러면 다음과 같이 이계상미분방정식 두개가 만들어집니다.
d 2 X d x 2 = k 2 X d 2 Y d y 2 = − k 2 Y (2-5) \tag{2-5}
\begin{align}
&{{d^2 X}\over{dx^2}} = k^2 X \\[10pt]
&{{d^2 Y}\over{dy^2}} = -k^2 Y\\
\end{align} d x 2 d 2 X = k 2 X d y 2 d 2 Y = − k 2 Y ( 2-5 ) 이때 위 (2-5)식의 첫번째 미분방정식의 일반해 는 아래 (2-6)식처럼 지수함수로 주어지고, 두번째 미분방정식은 단순조화진동자 운동방정식 풀이 처럼 진동함수로 주어집니다.
X ( x ) = A e k x + B e − k x Y ( y ) = C sin k y + D cos k y (2-6) \tag{2-6}
\begin{align}
& X(x) = Ae^{kx} + B e^{-kx}\\[10pt]
& Y(y) = C \sin ky + D \cos ky
\end{align} X ( x ) = A e k x + B e − k x Y ( y ) = C sin k y + D cos k y ( 2-6 ) 그러므로 위 (2-6)식을 (2-3)식의 형태로 표현하면 아래의 식을 도출할 수 있는데요. 이것이 일반해 입니다.
V ( x , y ) = X ( x ) Y ( y ) = ( A e k x + B e − k x ) ( C sin k y + D cos k y ) (2-7) \tag{2-7}
\begin{align}
V(x,y) &= X(x) Y(y)\\[10pt]
&= \big(A e^{kx} + B e^{-kx} \big) \big(C \sin ky + D \cos ky \big)
\end{align} V ( x , y ) = X ( x ) Y ( y ) = ( A e k x + B e − k x ) ( C sin k y + D cos k y ) ( 2-7 ) 지금까지 일반해를 구했으니 문제에 주어진 경계조건을 적용해서 특수해 도 구해 봐요. 즉 경계값 문제(boundary value problem) 를 풀어 위 식에서 A , B , C , D A,~B,~C,~D A , B , C , D
2-3. 라플라스방정식의 특수해 [세번째 경계조건 적용] 경계조건의 세번째는 x = ∞ x=\infty x = ∞ V ( x , y ) = 0 V(x,y) = 0 V ( x , y ) = 0 x = ∞ x=\infty x = ∞ X ( x ) X(x) X ( x )
X ( x ) = A e k × ∞ + B e − k × ∞ = 0 (2-8) \tag{2-8}
X(x) = Ae^{k\times \infty} + B e^{-k \times \infty} =0 X ( x ) = A e k × ∞ + B e − k × ∞ = 0 ( 2-8 ) 그러므로 위 (2-8)식이 성립하기 위해서는 가운데 부분의 둘째항은 0이므로 첫째 항도 0이 되어야 하는데 이를 만족하기 위해서는 A = 0 A=0 A = 0
앞서 말씀드린 것처럼 가운데 부분의 둘째 항은 경계조건에 따라 x = ∞ x=\infty x = ∞ e − k × ∞ e^{-k \times \infty} e − k × ∞ B B B
[첫번째 경계조건 적용] 또한 경계조건의 첫번째는 y = 0 y=0 y = 0 V ( x , y ) = 0 V(x,y) = 0 V ( x , y ) = 0 y = 0 y=0 y = 0 k y = 0 ky=0 k y = 0 Y ( y ) Y(y) Y ( y )
Y ( y ) = C sin 0 + D cos 0 = 0 (2-9) \tag{2-9}
Y(y) = C \sin 0 + D \cos 0 =0 Y ( y ) = C sin 0 + D cos 0 = 0 ( 2-9 ) 위 (2-9)식의 조건을 만족하기 위해서는 반드시 D = 0 D=0 D = 0 C C C
결국 (2-8)식과 (2-9)식에서 A = 0 A=0 A = 0 D = 0 D=0 D = 0
V ( x , y ) = ( B e − k x ) ( C sin k y ) = ( B C ) e − k x sin k y = E e − k x sin k y (2-10) \tag{2-10}
\begin{align}
V(x,y) &= (B e ^{-kx} ) (C \sin ky)\\
&=(BC) e^{-kx} \sin ky\\
&=E e^{-kx} \sin ky
\end{align} V ( x , y ) = ( B e − k x ) ( C sin k y ) = ( BC ) e − k x sin k y = E e − k x sin k y ( 2-10 ) 여기서도 E E E B B B C C C
[두번째 경계조건 적용] 이번에는 경계조건의 두번째, 즉 y = a y=a y = a V ( x , a ) = 0 V(x,a)=0 V ( x , a ) = 0
V ( x , a ) = E e − k x sin k a = 0 (2-11) \tag{2-11}
V(x,a) = E e^{-kx} \sin ka =0 V ( x , a ) = E e − k x sin ka = 0 ( 2-11 ) 여기서 E e − k x E e^{-kx} E e − k x k a = n π ka = n \pi ka = nπ n = 1 , 2 , 3 , ⋯ n=1,2,3, \cdots n = 1 , 2 , 3 , ⋯
그러므로 k = n π a k={{n \pi}\over{a}} k = a nπ n n n V ( x , y ) V(x,y) V ( x , y ) V n ( x , y ) V_n (x,y) V n ( x , y )
V n ( x , y ) = E n e − n π x / a sin n π a y = 0 , ( n = 1 , 2 , 3 , ⋯ ) (2-12) \tag{2-12}
\begin{align}
V_n(x,y) = E_n e^{-n \pi x /a} \sin {{n \pi}\over{a}} y =0,~~~~~~~(n=1,2,3,\cdots)
\end{align} V n ( x , y ) = E n e − nπ x / a sin a nπ y = 0 , ( n = 1 , 2 , 3 , ⋯ ) ( 2-12 ) 결국 윗식이 라플라스 방정식을 만족하므로 중첩과 선형성의 원리 에 따라 이 해들을 모두 선형결합한 것도 해가 됩니다. 이를 식으로 표현하면 다음과 같아요.
V ( x , y ) = c 1 V 1 ( x , y ) + c 2 V 2 ( x , y ) + c 3 V 3 ( x , y ) , ⋯ (2-13) \tag{2-13}
V(x,y) = c_1 V_1(x,y) + c_2 V_2(x,y) + c_3 V_3(x,y),\cdots V ( x , y ) = c 1 V 1 ( x , y ) + c 2 V 2 ( x , y ) + c 3 V 3 ( x , y ) , ⋯ ( 2-13 ) 여기서 c 1 , c 2 , c 3 , ⋯ c_1,~c_2,~c_3,~\cdots c 1 , c 2 , c 3 , ⋯ c 1 E 1 , c 2 E 2 , c 3 E 3 , ⋯ c_1 E_1, ~c_2 E_2, ~c_3 E_3,\cdots c 1 E 1 , c 2 E 2 , c 3 E 3 , ⋯
그래서 그 계수들의 곱을 G n G_n G n
V ( x , y ) = ∑ n = 1 ∞ G n e − n π x / a sin n π a y (2-14) \tag{2-14}
V(x,y) = \sum_{n=1}^{\infty} G_n e^{-n \pi x /a} \sin {{n \pi}\over{a}} y V ( x , y ) = n = 1 ∑ ∞ G n e − nπ x / a sin a nπ y ( 2-14 ) 하지만 아직까지 끝난게 아닙니다. G n G_n G n
이를 위해 (2-14)식의 양변에 sin m π y a \sin{{m \pi y}\over{a}} sin a mπ y y y y 0 ∼ a 0 \sim a 0 ∼ a
왜 이렇게 하냐면, 삼감함수의 직교성 이 나타나도록 식을 변형한 후 G n G_n G n
∫ 0 a V ( x , y ) sin m π y a d y = ∑ n = 1 ∞ G n e − n π x / a ∫ 0 a sin n π y a sin m π y a d y (2-15) \tag{2-15}
\int_0^aV(x,y) {\color{black} \sin{{m \pi y}\over{a}}dy} = \sum_{n=1}^{\infty} G_n e^{-n \pi x /a} {\color{blue} \int_0^a \sin {{n \pi y}\over{a}}} {\color{blue}\sin{{m \pi y}\over{a}}dy} ∫ 0 a V ( x , y ) s i n a mπ y d y = n = 1 ∑ ∞ G n e − nπ x / a ∫ 0 a s i n a nπ y s i n a mπ y d y ( 2-15 ) 윗 식의 우변을 보시면 파랑색 부분은 모두 y y y y y y
한편 삼각함수의 직교성에 따라 윗 식의 파랑색 부분은 m = n m=n m = n a 2 {{a}\over{2}} 2 a m ≠ n m \ne n m = n 크로네커 델타 기호 로 표시하면 다음과 같아요.
∫ 0 a V ( x , y ) sin m π y a d y = ∑ n = 1 ∞ G n e − n π x / a a 2 δ m n (2-16) \tag{2-16}
\int_0^aV(x,y) {\color{black} \sin{{m \pi y}\over{a}}dy} = \sum_{n=1}^{\infty} G_n e^{-n \pi x /a} {\color{blue} }{\color{red}{a \over 2}\delta_{mn}} ∫ 0 a V ( x , y ) s i n a mπ y d y = n = 1 ∑ ∞ G n e − nπ x / a 2 a δ mn ( 2-16 ) 윗식 좌변의 V ( x , y ) V(x,y) V ( x , y ) V ( x ) V ( y ) V(x) V(y) V ( x ) V ( y ) V ( x ) V ( y ) V(x) V(y) V ( x ) V ( y ) V 0 ( x ) V 0 ( y ) V_0(x) V_0(y) V 0 ( x ) V 0 ( y )
V 0 ( x ) ∫ 0 a V 0 ( y ) sin m π y a d y = ∑ n = 1 ∞ G n e − n π x / a a 2 δ m n (2-17) \tag{2-17}
{\color{blue}V_0(x)}\int_0^a V_0(y) {\color{black} \sin{{m \pi y}\over{a}}dy} = \sum_{n=1}^{\infty} G_n {\color{blue}e^{-n \pi x /a}} {\color{black}{{a}\over{2}}\delta_{mn}} V 0 ( x ) ∫ 0 a V 0 ( y ) s i n a mπ y d y = n = 1 ∑ ∞ G n e − nπ x / a 2 a δ mn ( 2-17 ) 그러면 윗 식에서 V 0 ( x ) V_0 (x) V 0 ( x ) x x x e − n π x / a e^{-n \pi x /a} e − nπ x / a
그러므로 e − n π x / a e^{-n \pi x /a} e − nπ x / a x = 0 x=0 x = 0 e − n π x / a = e 0 = 1 e^{-n \pi x /a} =e^0 = 1 e − nπ x / a = e 0 = 1 V 0 ( x ) = 1 V_0(x)=1 V 0 ( x ) = 1
이 관계를 반영하면 다음과 같습니다.
∫ 0 a V 0 ( y ) sin m π y a d y = ∑ n = 1 ∞ G n a 2 δ m n (2-18) \tag{2-18}
\int_0^a V_0(y) {\color{black} \sin{{m \pi y}\over{a}}dy} = \sum_{n=1}^{\infty} G_n {\color{re}{{a}\over{2}}\delta_{mn}} ∫ 0 a V 0 ( y ) s i n a mπ y d y = n = 1 ∑ ∞ G n 2 a δ mn ( 2-18 ) 자 이제 윗식의 우변을 검토해봐야 하는데요. 크로네커 델타의 성질 에 따라 m = n m=n m = n
∫ 0 a V 0 ( y ) sin m π y a d y = G n a 2 (2-19) \tag{2-19}
\int_0^a V_0(y) {\color{black} \sin{{m \pi y}\over{a}}dy} = G_n {a \over 2} ∫ 0 a V 0 ( y ) s i n a mπ y d y = G n 2 a ( 2-19 ) 이제 윗 식을 G n G_n G n m = n m=n m = n m m m n n n
G n = 2 a ∫ 0 a V 0 ( y ) sin n π y a d y (2-20) \tag{2-20}
G_n = {2 \over a}\int_0^a V_0(y) {\color{black} \sin{{n \pi y}\over{a}}dy} G n = a 2 ∫ 0 a V 0 ( y ) s i n a nπ y d y ( 2-20 ) 최종적으로 (2-2)식의 라플라스 방정식의 해는 다음과 같습니다.
V ( x , y ) = ∑ n = 1 ∞ G n e − n π x / a sin n π a y G n = 2 a ∫ 0 a V 0 ( y ) sin n π y a d y (2-21) \tag{2-21}
\begin{align}
&V(x,y) = \sum_{n=1}^{\infty} G_n e^{-n \pi x /a} \sin {{n \pi}\over{a}} y\\[10pt]
&~~~~~~~~G_n = {2 \over a}\int_0^a V_0(y) {\color{black} \sin{{n \pi y}\over{a}}dy}
\end{align} V ( x , y ) = n = 1 ∑ ∞ G n e − nπ x / a sin a nπ y G n = a 2 ∫ 0 a V 0 ( y ) s i n a nπ y d y ( 2-21 ) 2-4. 해를 그래프로 나타낸 모습 문제에 주어진 것처럼 V 0 ( y ) V_0(y) V 0 ( y ) G n G_n G n V 0 ( y ) V_0(y) V 0 ( y )
G n = 2 a V 0 ( y ) ∫ 0 a sin n π y a d y = 2 a V 0 ( y ) [ a n π ( − cos n π y a ) ] 0 a = 2 a V 0 ( y ) a n π ( 1 − cos n π ) = { 0 n = 짝수 4 V 0 ( y ) n π n = 홀수 (2-22) \tag{2-22}
\begin{align}
G_n &= {2 \over a} V_0(y) \int_0^a \sin {{n \pi y}\over{a}} dy\\[10pt]
&={2 \over a} V_0(y) \Big[ {a \over {n \pi}} \big(-\cos {{n \pi y}\over{a}} \big)\Big]_0^a\\[10pt]
&={2 \over {\cancel a}} V_0(y){{\cancel a} \over {n \pi}} \Big(1-\cos n \pi \Big)\\[10pt]
&=
\left\{
\begin{align*}
&0~~~~~~~~~~~~~~~~~~~~~~~~~n=짝수 \\
&{{4V_0(y)}\over{n \pi}}~~~~~~~~~~~~~~~n=홀수
\end{align*}
\right.
\end{align} G n = a 2 V 0 ( y ) ∫ 0 a sin a nπ y d y = a 2 V 0 ( y ) [ nπ a ( − cos a nπ y ) ] 0 a = a 2 V 0 ( y ) nπ a ( 1 − cos nπ ) = ⎩ ⎨ ⎧ 0 n = 짝수 nπ 4 V 0 ( y ) n = 홀수 ( 2-22 ) 결국 (2-21)식에 주어진 라플라스 방정식의 해 V ( x , y ) V(x,y) V ( x , y )
V ( x , y ) = 4 V 0 ( y ) π ∑ n = 1 , 3 , 5... ∞ 1 n e − n π x / a sin n π a y (2-23) \tag{2-23}
\begin{align}
&V(x,y) = {{4V_0(y)}\over{\pi}}\sum_{n=1, 3, 5...}^{\infty} {1 \over n} e^{-n \pi x /a} \sin {{n \pi}\over{a}} y\\[10pt]
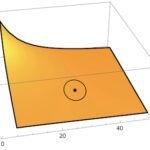
\end{align} V ( x , y ) = π 4 V 0 ( y ) n = 1 , 3 , 5... ∑ ∞ n 1 e − nπ x / a sin a nπ y ( 2-23 ) 아래 [그림 2]는 위 (2-23)식을 그래프로 그려 본 거에요. 직각좌표계에서의 라플라스방정식 해는 조화함수로 나타납니다. 이 조화함수의 특징 은 주어진 영역안에 극대나 극소가 나타나지 않으며, 극대와 극소는 주어진 영역의 테두리에만 존재하게 됩니다.
[그림 2] 문제로 주어진 접지된 두 평행판 사이의 전위 분포. 이 그래프는 매스매티카로 만들어졌으며 코드는 아래와 같습니다.
흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
![[그림 1] 직각좌표계에서의 라플라스방정식 예제. 접지된 두 평행판 사이의 전위 분포를 구하는 문제입니다.](https://ballpen.blog/wp-content/uploads/2024/12/라플라스방정식-예제-1.jpg)
![[그림 2] 문제로 주어진 접지된 두 평행판 사이의 전위 분포. 이 그래프는 매스매티카로 만들어졌으며 코드는 아래와 같습니다.](https://ballpen.blog/wp-content/uploads/2024/12/라플라스-방정식-해-1024x655.jpg)
