Last Updated on 2024-03-23 by BallPen
표준 오차를 도입하는 배경, 개념이 궁금합니다. 또한 표준 오차의 계산은 어떻게 할 수 있을까요?
표준 오차 개념을 이해하는 것은 측정값의 정확도를 올바르게 표기하는데 있어 아주 중요합니다. 계산은 비록 어렵지 않으나 그 개념을 이해하기는 쉽지 않습니다.
함께 표준 오차의 배경과 개념, 그리고 계산 방법을 알아보겠습니다. 목차는 다음과 같습니다.
Contents
1. 정확도와 정밀도의 계산과 표기 방법에 대한 복습
이전 포스트에서 측정 결과의 정확도와 정밀도에 대한 개념, 계산, 표기 방법에 대해 설명드린 바 있습니다. 간단히 복습을 하는 것이 표준 오차에 대한 이해도를 높일 수 있어요.
각각의 구체적인 계산법은 이전 포스트를 참고하세요.
1-1. 정확도
정확도는 측정값들이 한쪽으로 몰리는 일이 적은 정도를 나타내며, 표기하는 방법은 아래의 세가지 방법 중 하나를 적용하면 됩니다.
– 평균값과 참값의 백분율로 구하는 방법
측정값들의 평균값을 \mu, 참값을 X라 할때 정확도는 다음과 같습니다.
\tag{1} 정확도(\%) = {{\mu}\over{X}} \times 100
– 절대오차
측정값을 x, 참값을 X라 할 때 절대오차 \epsilon은 다음과 같습니다.
\tag{2} \epsilon = x-X
– 상대오차
상대오차 또는 백분율오차는 다음과 같습니다.
\tag{3} 상대오차(\%) = {{|\epsilon|}\over{X}} \times 100
1-2 정밀도
정밀도는 측정값들의 퍼짐이 좁은 정도를 나타내며, 표기하는 방법은 아래의 네가지 방법 중 하나를 적용하면 됩니다.
– 상대표준편차
측정값의 표준편차를 \sigma, 평균값을 \mu라 했을 때 상대표준편차 \% \mathrm{RSD}는 다음과 같습니다.
\tag{4} \% \mathrm{RSD} = {{\sigma}\over{\mu}} \times 100
– 측정값의 범위를 이용한 정밀도 계산과 표기
측정값의 최대값인 x(max)과 최소값인 x(min)으로 range를 구한 후 ‘평균값\pmrange’로 표기합니다.
\tag{5} Range = x(\mathrm{max})-x(\mathrm{min})
– 평균편차를 이용한 정밀도 계산과 표기
측정값을 x, 측정값의 평균을 \mu라 했을 때, 평균편차 \bar d를 계산한 후 ‘평균값\pm\bar d‘로 표기합니다.
\tag{6} \bar d = {{\Sigma |x-\mu|}\over{n}}
– 표준편차를 이용한 정밀도 계산과 표기
모집단 표준편차 \sigma 또는 표본 표준편차 s 를 계산한 후 ‘평균값\pm표준편차’로 표기합니다.
\begin{align}
\tag{7}
\sigma = \sqrt{{\Sigma (x-\mu)^2}\over{n}}= \sqrt{Var[x]} ~ (모집단 표준편차) \\
\end{align}\tag{8} s = \sqrt{{\Sigma (x-\mu)^2}\over{n-1}} ~ (표본 표준편차)
(7)식에서 주어진 Var[x]는 모집단의 x에 대한 분산을 뜻합니다.
2. 표준 오차 도입 배경
앞의 내용으로 이미 이해하셨겠지만 정확도는 오차로 평가되고, 정밀도는 편차로 평가됩니다.
또한 정밀도는 측정값들의 평균값과 결합하여 ‘평균값\pm정밀도’의 형식으로 표기되어 사람들에게 정밀한 정도에 대한 정보를 제공합니다. 물론 정밀도를 무엇으로 구했는지는 별도 표기를 해주어야 합니다.
그런데 여기서 한가지 궁금한 사항이 있습니다. 정확도에서 오차를 구하기 위해서는 참값이 필요한데 참값을 모르는 경우가 많습니다.
예를 들어 어느 물체가 있다고 하겠습니다. 그 물체의 질량을 알고 싶어 저울을 이용해 측정했습니다. 총 6번을 측정했어요.
12.0, 12.3, 11.8, 11.9, 12.4, 12.1 kg
위 측정 결과로부터 정밀도를 계산할 수 있을 것입니다. 또 평균값 \mu도 계산할 수 있어요.
그런데 오차의 범위는 어떻게 구할 수 있을까요? 참값을 우리가 알고 있다면 오차를 명확하게 구할 수 있을텐데요. 보통은 참값을 모르는 경우가 많습니다.
결국 우리가 어느 측정값을 표기하기 위해서는 정밀도 뿐만 아니라 오차의 범위도 제시할 필요가 있습니다. 왜냐하면 정확한 참값을 모르기 때문입니다. 이러한 배경에서 출발한 것이 표준오차가 되겠습니다.
3. 표준 오차 개념
어느 물체의 질량을 측정하기 위해 저울을 이용합니다. 이때 하나의 저울을 이용해 어느 사람이 측정한 값들의 세트인 X_1이 아래에 주어져 있습니다.
X_1 = {12.0, 12.3, 11.8, 11.9, 12.4, 12.1 kg}
이 값의 평균은 12.1 kg 입니다. 이 값이 참값일까요? 아닙니다. 바로 이 값들에는 계통오차가 들어가 있기 때문에 참값이라고 할 수 없습니다. 그렇다면 계통오차를 제거하여 참값을 도출하는 방법은 무엇일까요? 바로 아래에서 설명할 표본 평균의 평균이라는 값을 이용합니다.
그렇다면 표본 평균의 평균을 참값으로 간주한다면 위에서 측정한 측정값들의 표준편차를 구할 수 있을 것입니다. 이것이 표준 오차(Standard Error of Mean, SEM, 평균오차로 불리기도 함)입니다.
우선 단계적으로 표본 평균의 평균을 구하는 방법을 설명드리고 표준오차를 정의하는 방법을 구체적으로 설명드립니다.
3-1. 표본 평균의 평균
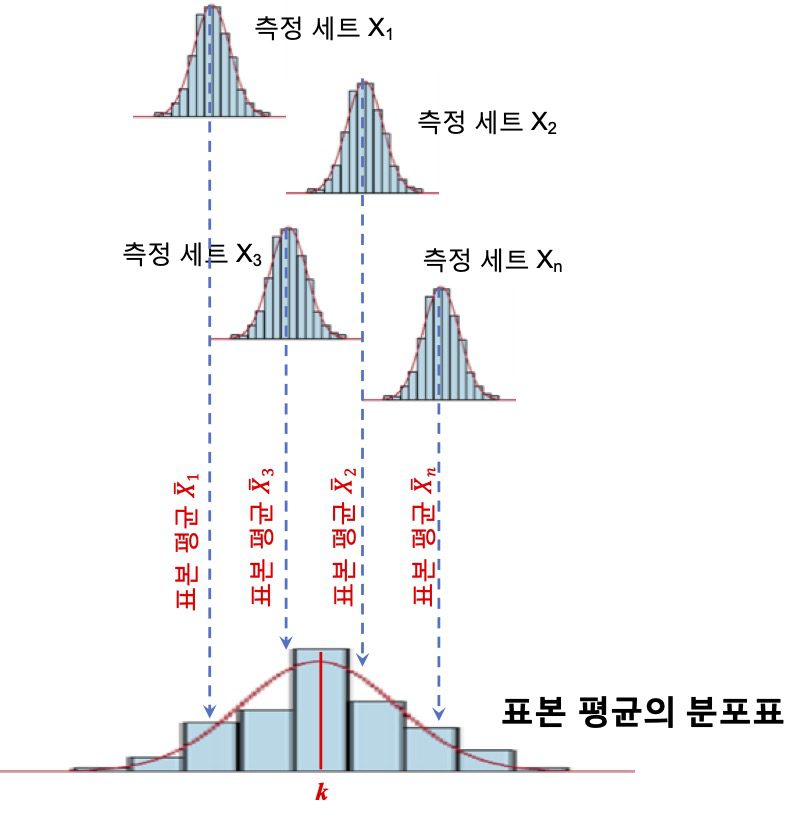
- (1단계) n명의 사람들이 자신의 저울을 이용하여 각각 물체의 질량을 n번 측정한다고 생각하세요. 그러면 n개의 표본이 생기는 것입니다. 그러면 X_1, X_2, X_3, \ldots, X_n의 측정값 세트가 존재하겠죠.
- (2단계) 각 측정값 세트의 평균을 내세요. 그러면 \bar{X}_1, \bar{X}_2, \bar{X}_3, \ldots, \bar{X}_n들이 구해질 것입니다. 이것이 표본 평균입니다.
- (3단계) 2단계에서 구한 표본 평균들의 평균을 구하세요. 그 값을 k라고 하고, 이 값이 표본 평균의 평균값입니다.
표본 평균의 평균 k는 n개의 표본으로부터 구한 평균값이기 때문에 각 표본이 갖는 계통오차들이 서로 상쇄되어 제거된 것으로 볼 수 있습니다.
즉 어느 표본에서 양의 계통오차가 발생했다면 다른 표본에서는 같은 크기의 음의 계통오차가 발생되어 서로 상쇄되어 제거되고 결국 참값만 남게 되는 원리이죠. 물론 많은 표본을 운영할 수록 참값에 가까워집니다.
그러므로 표본 평균의 평균 k를 개념적으로 참값으로 간주합니다.
3-2. 표준 오차 정의
표준 오차 SEM은 표본 평균에 대한 표준편차로 정의됩니다.
그러므로 (7)식의 모집단 표준편차 공식을 그대로 사용하는데요. 다만 변수 x 대신에 표본 평균 \bar{X}_1, \bar{X}_2, \bar{X}_3, \ldots, \bar{X}_n가 적용되고, 평균값 \mu 대신에 표본 평균의 평균 k가 적용됩니다.
이를 식으로 표현하면 다음과 같습니다.
\begin{align}
\tag{9} SEM &= \sqrt{{\Sigma (\bar{X} - k)^2}\over{n}} \\[10pt]
&=\sqrt{Var{\bar{\big[ X \big]}}}
\end{align}(9)식에서 Var\big[ \bar{X} \big]를 분산이라고 합니다. 결국 표준 오차는 반복실험으로 구해진 표본 평균들이 k로부터 어느 정도 흩어져 있는가의 척도인 것입니다.
4. 표준 오차 공식과 모집단 표준 편차 추청
(9)식을 이용하면 표준 오차 SEM을 구할 수 있습니다. 물론 많은 반복 실험 세트를 통해 k를 구하고 각 실험세트당의 표본 평균 \bar{X}를 구한 후 (9)식에 적용하면 됩니다.
그렇다면 단지 하나의 실험세트만 있을 때에는 어떻게 표준 오차를 구할 수 있을까요? 이러한 경우가 실험 현장에서 사실 많습니다.
이럴 때는 바로 측정값으로부터 모집단의 표준 오차 \sigma를 추정하는 방법으로 구합니다. 구체적인 내용은 아래에 설명드립니다.
4-1. 표준 오차 공식의 일반화
일단 통계학적인 수식 처리과정을 거쳐 보겠습니다. 흐름은 위에서 개념 설명할 때와 같습니다.
n개의 표본에서 각각 n개의 측정이 이루어집니다. 그러면 i번째 표본에서 도출된 측정세트는 X_i이고 이러한 것들이 n개가 있는 것입니다.
한 표본에서의 평균인 \bar{X}는 아래와 같이 구해집니다.
\tag{10} \bar{X}={{1} \over {n}} \sum_{i=1}^{n} X_i
표준 오차의 정의 식인 (9)식에서 근호안에 있는 분산을 우선 표현하면 다음과 같습니다.
\begin{align}
\tag{11} Var \big[ \bar{X} \big] &= Var \Big[ {{1}\over{n}} \sum_{i=1}^n X_i \Big]\\[10pt]
&= Var \Big[ {{1}\over{n}} (X_1 + \ldots + X_n) \Big] \\[10pt]
&= {{1}\over{n^2}} Var[X_1 + \ldots + X_n] \\[10pt]
&= {{1}\over{n^2}} \times \big( n \times Var[X] \big) \\[10pt]
&= {{1}\over{n}} Var[X]
\end{align}(11)식 전개 과정에서 다음의 성질이 이용되었습니다.
\tag{12} Var[aX+b] = a^2 Var[X]
\begin{align}
\tag{13} Var[X_1 + \ldots + X_n ] &= Var[X_1] + \ldots + Var[X_n] \\[10pt]
&= n \times Var[X]
\end{align}이때 (13)식에서 Var[X]는 모집단의 분산을 뜻합니다. 이것은 n이 크다면 모집단으로부터 추출되는 각 표본에서의 분산은 모집단의 분산과 같다는 통계학적 의미가 반영된 것입니다.
(7)식과 (11)식을 이용하여 (9)식의 표준 오차 SEM을 정리하면 아래와 같습니다.
\begin{align*}
SEM &= \sqrt{Var[\bar{X}]} = \sqrt{{{1}\over{n}} Var[{X}]} \\[10pt]
&= \sqrt{{\Sigma({x} - \mu)^2}\over{n\times n}} \\[10pt]
&= {{\sigma}\over{\sqrt{n}}}
\end{align*}결국 표준 오차 SEM은 모집단의 표준편차 \sigma를 \sqrt{n}으로 나누면 간단히 구해집니다.
그런데 문제는 모집단의 표준편차 \sigma를 어떻게 구하느냐인데요.
보통은 모집단의 표준편차를 구하지 못하니 표본 측정값들의 표준편차 s를 구하고 이것을 모집단의 표준편차 \sigma의 추정치로 활용하게 됩니다.
결국 실험세트가 단지 하나인 경우에 SEM은 아래와 같이 구합니다.
\tag{14} SEM = {{s}\over{\sqrt{n}}}
4-2. 표준 오차 SEM을 이용한 측정값의 표기
그렇다면 측정값을 표기할 때 (9) 또는 (14)식으로 구한 표준오차 SEM을 어떻게 활용할까요?
정밀도를 표현할 때와는 약간 다릅니다. 즉 “평균값\pm(Z-score \times SEM)”를 활용하는데요.
\tag{15} \bar{X} \pm Z{{s}\over{\sqrt{n}}}
이 식에서 Z는 90% 신뢰수준의 경우 1.65, 95% 신뢰수준의 경우 1.96, 99% 신뢰수준의 경우 2.58을 적용합니다. 연구에서는 보통 95% 신뢰수준을 적용합니다.
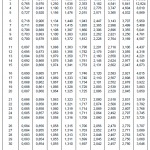
정규분포표의 Z값을 적용하는 것은 실험세트의 측정값이 100개 이상인 경우에 보통 적용합니다. 만일 측정값이 100개 미만인 경우에는 (15)식에서 Z대신에 t분포값이 들어갑니다.
예를 들어 95% 신뢰수준에서 측정값이 5개 뿐인 경우에는 아래 (16)식과 같이 표기합니다. t분포표 보는 방법은 여기를 클릭하세요.
\tag{16} \bar{X} \pm 2.776 {{s}\over{\sqrt{n}}}
아울러 사람들이 평균값 \bar{X} 뒤에 쓰여진 것이 정밀도인지 아니면 표준오차인지를 헷갈릴 수 있으므로 반드시 표기해주어야 합니다.
5. 표준 오차 계산 방법 예제
6. 표준 오차 개념, 공식, 계산 방법의 정리
- 표준 오차 (또는 평균 표준 오차)란 표본 평균에 대한 표준편차이다.
- 오차 용어를 사용하는 이유는 표준 오차 공식에서, 표본 평균의 평균값 k를 참값으로 간주하고 표본 평균과의 차이인 오차 개념이 적용되기 때문이다.
- 표준오차는 측정값의 표준편차를 구한 후 그 값을 \sqrt{n}으로 나누면 간단히 구할 수 있다.
- 반복실험에 의해 측정값이 100회 이상인 경우에는 정규분포의 신뢰수준에 따른 측정값 표기방식을 따르고 100회 미만인 경우에는 t-분포표에 따른 표기방식을 따른다.
- 만일 측정값이 단지 5개 미만이라면 무리해서 표준 오차를 구하는 것보다는 평균치와 표준편차를 그대로 보여주는 것이 좋다.






nice