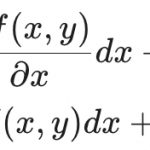Last Updated on 2024-01-06 by BallPen
1계 선형 미분방정식의 풀이 원리를 이해하고 예제를 풀어봅니다.
1계 선형 미분방정식(First Order Linear Differential Equations) 이란 종속변수가 한번 미분되고, 종속변수와 그 도함수의 계수가 독립 변수에만 의존하는 미분방정식을 말합니다.
그리고 위 조건에 부합하는 미분방정식을 특별한 형태로 정리한 것을 ‘1계 선형 미분방정식의 표준형’이라고 합니다.
이번에는 1계 선형 미분방정식의 표준형을 어떻게 푸는지 그 원리를 알아보겠습니다.
아래는 이번 글의 목차입니다
Contents
1. 1계 선형 미분방정식 표준형
앞에서 말씀드렸듯이 1계 선형 미분방정식을 특별한 형태로 표현한 것을 ‘1계 선형 미분방정식의 표준형’이라고 하며 다음의 모양을 갖습니다.
\tag{1}
{{dy \over dx} + p(x)y = r(x)}(1)식과 같이 표준형은 종속변수 y의 1계 도함수로 구성되어 있으면서, 종속변수의 계수가 독립변수 x의 함수로 이루어져 있어요.
이때 우변이 r(x)=0이면 ‘제차형 1계 선형 미분방정식’이라 하고, r(x) \ne 0이면 ‘비제차형 1계 선형 미분방정식’이라 합니다.
그러면 다음 식의 1계 선형 미분방정식을 표준형으로 바꾸어 보세요. 여기서 표준형으로 굳이 바꾸는 이유는 1계 선형 미분방정식의 해법이 표준형에 맞추어져 있기 때문이에요.
\tag{2}
x {dy \over dx} - 4 y = x^6 e^x(2)식을 표준형으로 바꾸면 다음과 같습니다. dy / dx의 계수인 x로 양변을 나누면 되는 거죠.
\tag{3}
\begin{align}
{dy \over dx} - {4 \over x}y = x^5 e^x
\end{align}(3)식의 -4 / x는 표준형에서 p(x)에 해당하고, x^5 e^x는 r(x)에 해당합니다.
2. 1계 선형 미분방정식 풀이 방법
지금까지 1계 선형 미분방정식의 표준형에 대해 알아봤습니다. 이제부터는 이 미분방정식의 풀이 방법을 알아보죠.
제차형과 비제차형을 구분하여 설명드립니다.
2-1. 제차형 1계 선형 미분방정식
제차형 1계 선형 미분방정식의 표준형은 다음과 같습니다.
\tag{4}
{dy \over dx} + p(x)y =0이 식을 풀기 위해서는 변수분리형 미분방정식 풀이 방법 처럼 (4)식을 다음과 같이 변수분리합니다.
\tag{5}
{1 \over y} dy = -p(x)dx그리고는 (5)식의 양변을 적분합니다.
\tag{6}
\int {1 \over y} dy = - \int p(x)dx\ln {|y|} +c_1 = - \int p(x)dx\ln |y| = -\int p(x)dx +(-c_1)
그리고 양변에 exponential을 취합니다. 이때 상수 c_1에 음수가 붙은 것도 또하나의 상수일 뿐이므로 이를 c_2로 표현하였습니다.
\tag{7}
\begin{align}
y &= e^{- \int p(x)dx + c_2}\\
&=e^{c_2} e^{-\int p(x)dx}
\end{align}여기서도 상수 c_2에 exponential을 취한 e^{c_2}도 또 하나의 상수가 될 뿐입니다. 그래서 e^{c_2}를 c로 바꿀 수 있습니다.
결국 (4)식의 일반해는 다음과 같습니다.
\tag{8}
y = c e^{-\int p(x)dx}물론 상수 c는 초기조건이 주어지면 구할 수 있습니다.
2-2. 비제차형 1계 선형 미분방정식
비제차형 1계 선형 미분방정식의 표준형은 다음과 같습니다.
\tag{9}
{dy \over dx} + p(x)y = r(x)그러면 (9)식을 다음과 같이 정리할 수 있을 거에요.
p(x)y-r(x) = -{dy \over dx}\\
\tag{10}
\Big(p(x)y - r(x) \Big) dx + dy = 0(10)식을 자세히 보면 완전미분방정식의 형태를 갖습니다. 그런데 이것이 정말 완전미분방정식인지 아니면 불완전미분방정식인지 확인해 볼 필요가 있어요.
이 확인방법이 잘 기억나지 않으면 완전미분방정식 풀이 방법을 참고하시기 바랍니다.
우선 (10)식을 다음과 같이 표현해볼께요.
\tag{11}
M(x,y) dx + N(x,y) dy =0그리고 M(x,y)와 N(x,y)를 각각 y와 x로 편미분 합니다. 그리고 그 두 결과가 서로 같으면 (10)식은 완전미분방정식이라는 의미를 갖죠.
확인해 보겠습니다.
\tag{12}
{{\partial M(x,y)} \over {\partial y}} = {{\partial \big(p(x)y - r(x)\big)}\over{\partial y}} = p(x)\tag {13}
{{\partial N (x,y)}\over{\partial x}} = {{\partial 1}\over{\partial x}} = 0그 결과 (12)식과 (13)식을 비교해 보니 그 결과값이 서로 다르다는 것을 알 수 있습니다. 이것은 (10)식이 완전미분방정식이 아닌 불완전미분방정식임을 뜻해요.
이제부터는 불완전미분방정식 풀이 방법을 적용합니다. 여기서는 적분인자가 x만의 함수로 되어 있다고 해보겠습니다.
[적분인자 구하기]
불완전미분방정식 풀이 방법에 따르면 적분인자 F(x)는 다음과 같습니다.
\tag{14}
F(x) = \exp\Big( \int {{1}\over{N(x,y)}} \big( {{\partial M (x,y)}\over{\partial y}} - {{\partial N(x,y)}\over{\partial x}} \big) dx \Big)(14)식에 관련된 요소들을 대입하여 적분인자를 구합니다.
\tag{15}
\begin{align}
F(x) &= \exp \Big( \int {1 \over 1} \big( {{\partial(p(x)y - r(x))}\over{\partial y}} - {{\partial 1}\over{\partial x}} \big) dx \Big)\\
&=\exp \Big(\int p(x) dx \Big)
\end{align}[적분인자로 일반해 구하기]
(15)식과 같이 적분인자를 구했으니 이제 일반해를 구하면 됩니다. 이를 위해 (15)식의 적분인자를 (9)식의 양변에 각각 곱하고 정리합니다.
우선 좌변부터 정리해볼께요.
\tag{16}
\begin{align}
e^{\int p(x)dx} \Big( {{dy}\over{dx}} + p(x)y\Big) = {dy \over dx} e^{\int p(x) dx} + \color {blue}y p(x)e^{\int p(x)dx}
\end{align}이때 e^{\int p(x)dx}를 e^t로 치환하고, 그리고 e^t를 g로 다시 한번 더 치환하겠습니다. 그리고 g를 x로 미분하면 다음과 같습니다.
\tag{17}
\begin{align}
{d \over dx}(e^{\int p(x)dx} )= {d e^t \over dx}= {dg \over dx} = {dg \over dt} {dt \over dx} &= e^t {d \over dx} (\int p(x)dx)\\
&=e^{\int p(x) dx} p(x)
\end{align}(17)식의 결과를 (16)식의 파랑색 부분에 대입합니다. 그러면 다음과 같이 정리될 수 있어요.
\tag{18}
\begin{align}
e^{\int p(x)dx} \Big( {{dy}\over{dx}} + p(x)y\Big) &= {dy \over dx} e^{\int p(x) dx} + \color {blue}y p(x)e^{\int p(x)dx}\\
&={dy \over dx} e^{\int p(x) dx} + y {{d}\over{dx}}(e^{\int p(x)dx})\\
&={d \over dx} \big( y e^{\int p(x)dx}\big)
\end{align}이번에는 (15)식의 적분인자를 (9)식의 우변에 곱해 줍니다. 그러면 다음과 같아요.
\tag{19}
e^{\int p(x)dx} r(x)이제 (18)식과 (19)식은 서로 같아야 합니다. 왜냐면 (9)식의 양변에 동일한 적분인자를 각각 곱해주었기 때문이죠.
두 식을 같게 놓으면 다음과 같습니다.
\tag{20}
\begin{align}
&{d \over dx} \big( y e^{\int p(x)dx} \big) = e^{\int p(x)dx} r(x)\\
&d \big( e^{\int p(x)dx} y\big) = e^{\int p(x)dx} r(x) dx
\end{align}그리고 (20)식의 양변을 적분해봐요.
\tag{21}
\begin{align}
\int d\big( e^{\int p(x)dx}y \big) = \int e^{\int p(x)dx} r(x) dx + C
\end{align}\tag{22}
\begin{align}
e^{\int p(x)dx}y = \int e^{\int p(x)dx} r(x) dx + C
\end{align}여기서 C는 적분상수입니다. 그리고 y에 대해 정리해 보세요. 그것이 바로 비제차형 1계 선형 미분방정식의 일반해가 됩니다.
바로 아래 식이 그 일반해입니다.
\tag{23}
y = e^{- \int p(x)dx} \Big[ \int e^{\int p(x)dx} r(x) dx + C \Big]3. 1계 선형 미분방정식 풀이 예제
예제를 하나 풀어보겠습니다. 다음 미분방정식을 풀어보세요.
\tag{q-1}
{dy \over dx} - y = e^{2x}이 미분방정식은 1계 선형 미분방정식입니다. 따라서 (23)식을 사용하면 쉽게 일반해를 구할 수 있어요.
이때 1계 선형 미분방정식 표준형에서 p(x) = -1 이고, r(x) = e^{2x}입니다.
\tag{q-2}
\begin{align}
y &= e^{- \int p(x)dx} \Big[ \int e^{\int p(x)dx} r(x) dx + C \Big]\\
&=e^{-\int (-1) dx} \Big[ \int e^{\int (-1) dx} e^{2x} dx + C \Big]\\
&=e^x \Big[ \int e^{-x} e^{2x} dx + C \Big]\\
&=e^{x} \Big[e^{x} +C \Big]\\
&=e^{2x} + Ce^{x}
\end{align}이 식에서도 C는 상수로서 초기조건을 이용해 구하면 됩니다.
