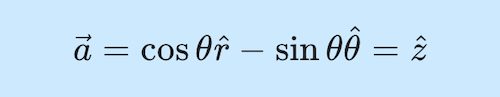Last Updated on 2025-12-15 by BallPen
구면좌표계에서 정의된 벡터를 직각좌표계로 표현해 봐요.
벡터의 좌표계 변환 예제를 풀어 보겠습니다.
아래에 구면좌표계에서 정의된 벡터 \vec a가 있어요.
\tag{1}
\vec a = \cos \theta \hat r - \sin \theta \hat \theta
이 벡터를 직각좌표계로 바꾸어 표현해 보겠습니다.
이를 위해서는 구면좌표계의 단위벡터를 직각좌표계로 표현한 아래의 관계식이 필요합니다.
\tag{2}
\begin{aligned}
&\hat r = \sin \theta \cos \phi \hat x + \sin \theta \sin \phi \hat y + \cos \theta \hat z\\[7pt]
&\hat \theta = \cos \theta \cos \phi \hat x + \cos \theta \sin \phi \hat y - \sin \theta \hat z\\[7pt]
&\hat \phi = - \sin \phi \hat x + \cos \phi \hat y
\end{aligned}(2)식의 \hat r과 \hat \theta를 (1)식에 대입하세요.
\tag{3}
\begin{aligned}
\vec a &= \cos \theta \hat r - \sin \theta \hat \theta\\[7pt]
&=\cos \theta(\sin \theta \cos \phi \hat x + \sin \theta \sin \phi \hat y + \cos \theta \hat z) \\[7pt]
&~~~~~~~~~~~~~~~- \sin \theta(\cos \theta \cos \phi \hat x + \cos \theta \sin \phi \hat y - \sin \theta \hat z)\\[7pt]
&=\cos^2 \theta \hat z + \sin^2 \theta \hat z\\[7pt]
&=(\cos^2 \theta + \sin^2 \theta)\hat z\\[7pt]
&=\hat z
\end{aligned}결국 (1)식의 벡터는 직각좌표계에서의 z방향 단위벡터와 같다는 것을 알 수 있어요.
흥미롭고 도움이 되는 글이었나요? 리뷰를 부탁드립니다.
[Total: 1 Average: 5]