정상전류

Last Updated on 2025-09-12 by BallPen

연속방정식과 정상전류의 요건을 알아 봐요.

정상전류(steady current)란 전하의 흐름 양이 늘어나거나 줄지도 않고, 영원히 계속되는 전류를 말해요.

이 글에서는 연속방정식을 유도한 후 정상전류 요건을 알아 보겠습니다.

결론부터 말씀드리면 연속방정식이란 다음 식을 뜻해요. \vec J는 전류밀도, \rho는 부피전하밀도를 뜻합니다.

\begin{align}
\tag{D1}
\nabla \cdot \vec J = - {{\partial \rho}\over{\partial t}}
\end{align}

그리고 정상전류일 요건은 다음과 같아요.

\begin{aligned}
\tag{D2}
&{{\partial \rho}\over{\partial t}} = 0\\[15pt]
&\nabla\cdot \vec J =0
\end{aligned}

보다 구체적인 내용은 본문을 참고하시기 바랍니다.

1. 연속방정식

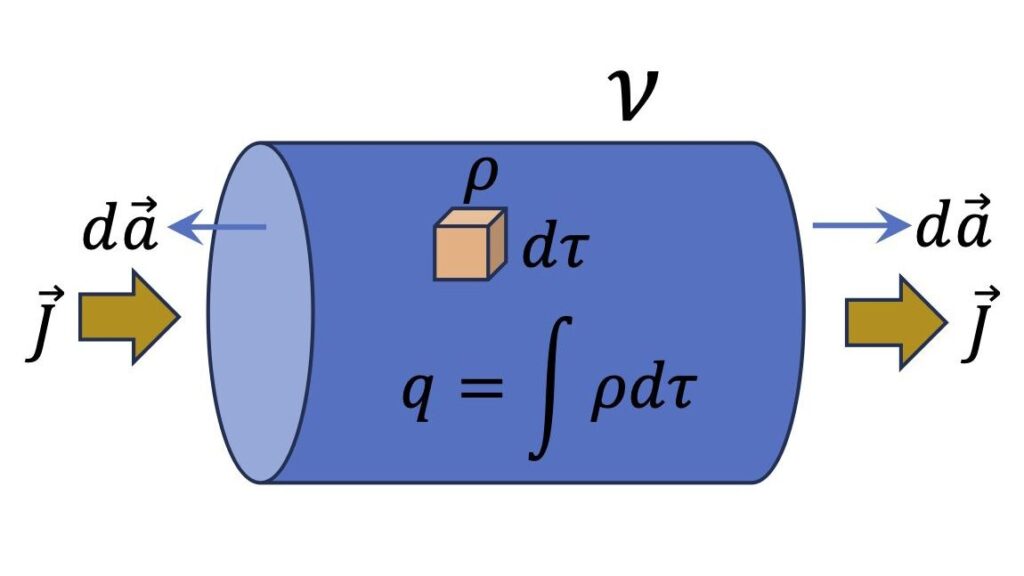
아래 [그림 1]에 원통형 물체가 있는데요. 전하량 q가 전체 부피 \nu에 분포하고 있다고 생각해봐요.

이때 미소 부피 요소를 d \tau라 하고, 부피 전하 밀도를 \rho라 하겠습니다.

그러면 원통형 물체 안에 있는 총전하량 q는 다음과 같아요.

\begin{align}
\tag{1-1}
q = \int_\nu \rho d\tau
\end{align}

그런데 이 전하가 원통의 닫혀진 면을 통과해 빠져나간다고 생각해봐요. 물론 원통에는 여러 면들이 있는데요.

그 중에서 그림처럼 오른쪽 면으로만 전하가 빠져나가는데, 빠져나가는 전류밀도를 \vec J라고 해봐요. 그리고 오른쪽 면의 면적벡터를 d \vec a라고 하겠습니다.

그러면 원통의 닫혀진 전체 면을 통과해 빠져나가는 전류 I는 다음과 같이 쓸 수 있어요.

\begin{align}
\tag{1-2}
I= \oint_s \vec J \cdot d\vec a
\end{align}

그리고 윗 식의 오른 쪽 항에 발산 정리를 적용하면 다음 식이 성립합니다.

\begin{align}
\tag{1-3}
I= \oint_s \vec J \cdot d\vec a = \int_\nu (\nabla \cdot \vec J) d \tau
\end{align}

또한 전류에 대한 기본 정의 식인 I = {dq/dt}에서 전하량 q에 (1-1)식을 대입하면 (1-3)식의 전류 I는 다음과 같이 쓸 수도 있어요.

\begin{align}
\tag{1-4}
I = - {{dq}\over{dt}} = -{{d}\over{dt}} \int_\nu \rho d\tau = - \int_\nu \Big({{\partial \rho}\over{\partial t}}\Big) d \tau
\end{align}

이때 윗 식에서 음의 부호는 전류 I가 흐를 수록 원통형 물체 내의 총 전하량 q가 감소해야하므로 일부러 부여한 것입니다.

그러면 (1-3)식과 (1-4)식은 서로 같아야 하므로 아래 식이 성립함을 알 수 있어요.

\begin{align}
\tag{1-5}
\nabla \cdot \vec J = - {{\partial \rho}\over{\partial t}}
\end{align}

이 식을 연속방정식(continuity equation)이라 부릅니다.

연속방정식은 전류밀도의 발산은 부피 전하 밀도의 감소를 일으킨다는 것을 의미하는 식이에요. 이는 전하보존법칙을 수식으로 표현한 것으로 볼 수 있어요.

2. 정상전류

정상전류란 전류가 정상이냐 비정상이냐의 의미가 아니에요. 정상 전류란 전하의 흐름 양이 늘어나거나 줄지도 않고, 영원히 계속되는 전류를 의미해요.

예를 들어 [그림 1]과 같이 원통에서 전류밀도가 빠져나간다면 (1-5)식에 따라 부피전하밀도의 감소가 일어나야 합니다. 그래서 충분한 시간이 지나면 결국 원통내의 모든 전하가 빠져나가게 되고 더이상 전하 흐름이 존재할 수 없을 거에요.

그러므로 이 경우에는 정상전류가 아닙니다.

하지만 아래 [그림 2]와 같이 오른쪽 면으로 전류밀도가 흘러나가는 동시에 왼쪽에서 동일한 크기의 전류밀도가 유입된다고 생각해 봐요.

그러면 원통형 물체(도선) 입장에서는 왼쪽으로 들어오는 음의 전류(\vec J와 d \vec a의 방향이 반대이므로)와 오른쪽으로 나가는 양의 전류(\vec J와 d \vec a의 방향이 평행하므로)를 합하면 (1-2)식으로 주어지는 알짜 전류 I는 0이 됩니다.

그러면 (1-3)식과 (1-4)식이 모두 0을 만족해야 하므로 결국 다음 조건이 성립해야 함을 이해할 수 있어요. 그리고 이 조건을 만족하는 전류를 정상전류라고 해요.

\begin{aligned}
\tag{1-6}
{{\partial \rho}\over{\partial t}} =0\\[15pt]
\nabla \cdot \vec J = 0
\end{aligned}

윗 식은 정상전류가 도선에 흐른다면 부피 전하 밀도가 상수가 되어 시간에 따라 달라지지 않음을 뜻해요. 또한 전류밀도 \vec J의 발산이 0이 됨을 의미합니다.

Related posts.

정상전류에 의한 자기장 자동차의 최고출력 개념과 이 값이 크면 무엇이 좋은가? 질량과 무게 – 전자 저울로 측정한 값은 질량일까요 무게일까요? 가속도 운동 – 음의 가속도, 0의 가속도, 양의 가속도 개념 정리 벡터, 벡터의 작도, 벡터의 크기, 벡터의 성분 벡터의 덧셈 : 기하학적 표현과 수학적 처리 회전운동 – 각위치, 각변위, 각속도, 각가속도의 정의와 개념 높이에 따른 위치에너지 변화