BallPen

우함수와 기함수
5 (1)

작성자:

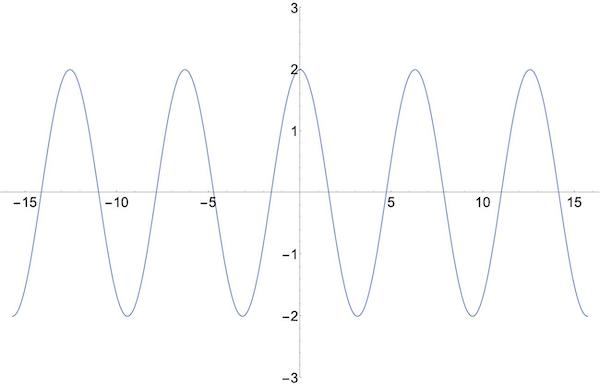
함수의 대칭성을 표현하는 우함수(짝함수)와 기함수(홀함수)에 대해 명확히 구분해 봐요. 우함수와 기함수 개념은 함수의 대칭성을 기준으로 구분합니다. 이에 대해 자세히 알아 봐요. Contents1. 우함수(Even Function, 짝함수)2. 기함수(Odd Function, 홀함수)3. 요약 1. 우함수(Even Function, 짝함수) 우함수는 그래프가 y축에 대해 대칭인 함수예요. 쉽게 말해 y축을 중심으로 데칼코마니처럼 접으면 완전히 겹쳐지는 모양이죠. 2. 기함수(Odd Function, 홀함수) 기함수는 그래프가 원점에 대해 대칭인 … Read more

척력장 내의 운동 궤도
5 (1)

작성자:

입자가 역제곱 중심력장내에서 척력을 받을 때 입자의 운동 궤도를 알아 봐요. 척력장 내에서 입자가 역제곱 중심력을 받을 때 입자의 궤도를 알아 보겠습니다. 이것은 알파입자 산란 실험과 같이 양전하인 알파입자가 양전하를 띤 원자핵 주변을 지날 때 갖는 궤도로 생각하면 됩니다. 궤도를 구하기 위해서는 중심력장 하에서 입자의 궤도방정식을 풀면 되는 데요. 결과부터 말씀드리면 척력장에서 입자 궤도의 이심률 … Read more

여러 서버로 SSH 접속 방법
5 (1)

작성자:

로컬컴퓨터에서 여러 서버로 SSH 접속하는 방법을 알아 봐요. 1. 문제 상황 SSH로 로컬 컴퓨터에서 원격 서버에 접속하는 방법을 설명드린 적이 있어요. 그런데 이 방법은 한 대의 서버에 대해서만 접속할 수 있습니다. 그러니까 로컬 컴퓨터로 서버A와 B를 접속하고 싶은 경우가 있을 수도 있는데요. 이게 되지 않아요. 그 이유는 서버 A에 접속하기 위해 ssh-keygen 명령어로 개인키와 공개키를 … Read more

자기장의 회전
5 (1)

작성자:

앙페르 법칙으로 불리는 자기장의 회전에 대해 알아 봐요. 자기장의 회전 를 구해 보겠습니다. 이 개념도 아주 중요한데요. 결론부터 말씀드리면 자기장의 회전은 다음과 같습니다. 여기서 는 전류밀도를 의미해요. 그리고 윗 식에 스토크스 정리(Stokes’ theorem)를 적용하면 다음 식이 성립합니다. 이 결과들은 패러데이 법칙과 비교해보면 아주 재미있어요. 구체적인 내용은 본문에서 설명드리겠습니다. 아래는 이번 글의 목차입니다. Contents1. (복습) 일정한 … Read more

정상전류
5 (1)

작성자:

연속방정식과 정상전류의 요건을 알아 봐요. 정상전류(steady current)란 전하의 흐름 양이 늘어나거나 줄지도 않고, 영원히 계속되는 전류를 말해요. 이 글에서는 연속방정식을 유도한 후 정상전류 요건을 알아 보겠습니다. 결론부터 말씀드리면 연속방정식이란 다음 식을 뜻해요. 는 전류밀도, 는 부피전하밀도를 뜻합니다. 그리고 정상전류일 요건은 다음과 같아요. 보다 구체적인 내용은 본문을 참고하시기 바랍니다. Contents1. 연속방정식2. 정상전류 1. 연속방정식 아래 [그림 … Read more

자기장의 발산
5 (1)

작성자:

자기에 대한 가우스 법칙으로 불리는 자기장의 발산에 대해 알아 봐요. 자기장의 발산 을 구해 보겠습니다. 이 개념은 자기장의 특성을 이해하는데 아주 중요합니다. 결론부터 말씀드리면 자기장의 발산은 0입니다. 그리고 윗 식에 발산 정리를 적용하면 다음 식이 성립합니다. 즉 닫혀진 곡면에 대한 자기장 선속은 0입니다. 가우스 법칙으로 설명되는 전기장의 발산과 비교하면 재미있을 거에요. 전기장의 발산과 달리 자기장의 … Read more

정상전류에 의한 자기장
5 (1)

작성자:

정상전류가 만드는 자기장을 비오-사바르 법칙으로 구해 봐요. 정상전류에 의한 자기장(또는 정상전류가 만드는 자기장)을 이번 글에서 알아 볼 거에요. 여기서 정상전류(steady current)란 도선에 흐르는 전류가 시간에 따라 변하지 않는 것을 뜻해요. 만일 시간에 따라 변하면 그것은 정상전류가 아니라 비정상전류라고 합니다. 한편 도선에 전류가 흐르면 그 주변에 자기장이 형성됩니다. 이때 정상전류에 의해 형성되는 자기장을 표현하는 법칙이 비오-사바르 … Read more

일계 미분 곱셈 규칙 : 벡터 미분 연산자
5 (1)

작성자:

벡터 미분 연산자를 이용한 일계 미분의 몇가지 곱셈 규칙을 알아 봐요. 일계 미분 곱셈 규칙 몇가지를 알아 봐요. 전자기학 등을 공부할 때 자주 등장하는 규칙들이에요. 참고로 몇가지 이계 미분 곱셈 규칙도 있으니 이것이 궁금하면 링크를 클릭하시기 바랍니다. 벡터 미분 연산자(또는 델연산자)가 사용된 일계 미분 곱셈 규칙은 다음과 같아요. 여기서 와 는 스칼라 함수이고 와 는 … Read more

행성 궤도의 에너지
5 (1)

작성자:

역제곱 중심력이 작용할 때 행성 궤도가 갖는 에너지를 구해 봐요. 행성 궤도의 에너지 크기는 행성이 타원궤도를 갖는지 아니면 포물선궤도나 쌍곡선궤도를 갖는지에 따라 달라집니다. 그리고 행성 궤도를 알기 위해서는 이심율 을 구해야 하는데요. 이심율은 행성의 궤도 방정식으로도 구할 수 있지만 이 글에서 소개하는 궤도의 에너지 방정식을 통해 구할 수도 있어요. 궤도의 에너지 방정식은 다음과 같아요. 여기서 … Read more